Count on a Tree - 2

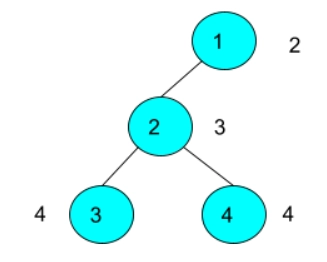
Intuition

We can simply use a DFS Algorithm(Depth First Search) function to find the path between two nodes given in the query and then store them in a vector. After storing all the nodes on the path, we can just find the distinct values among them. We can understand the algorithm from below.

Check out Euclid GCD Algorithm

Algorithm

The algorithm to solve the above problem is as follows:

• After taking input and constructing the tree, we will start answering queries.
• We can now run the function dfs() with node ‘p’ of the current query as its argument, and after obtaining the path, we will store it in a vector ‘pathNodes’.
• Then we will find the distinct elements from this vector ‘pathNodes’ and store the count in the variable ‘cnt’. 
• Finally, we will output the answer stored in the variable ‘cnt’ and move to the next query. 

The implementation of the above algorithm is as follows.

Implementation

// Program to find the number of distinct values on a path.
#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

// Data structures required.
int N, Q, x, y, cnt;
vector<vector<int>> tree;
vector<int> val, vis, path;
unordered_map<int, int> over;

// Depth First Search.
void dfs(int node, int par, int tgt)
{
      vis[node] = 1;

      // If reached the second node.
      if (node == tgt)
      {
            for (int i = 1; i <= N; i++)
            {
                  if (vis[i] == 1)
                        path.push_back(i);
            }
            return;
      }

      for (auto x : tree[node])
      {
            if (x != par)
                  dfs(x, node, tgt);
      }
      vis[node] = 0;
}

// Main Function.
int main()
{
      // Input of number of nodes and queries.
      cin >> N >> Q;

      // Resizing vectors according to the input.
      val = vector<int>(N + 1);
      tree = vector<vector<int>>(N + 1, vector<int>(0));

      // Input of values of nodes.
      for (int i = 1; i <= N; i++)
            cin >> val[i];

      // Constructing the tree.
      for (int i = 0; i < N - 1; i++)
      {
            cin >> x >> y;
            tree[x].push_back(y);
            tree[y].push_back(x);
      }

      // Solving queries.
      for (int i = 0; i < Q; i++)
      {
            // Input of nodes.
            cin >> x >> y;

            // Setting up data structures.
            vis = vector<int>(N + 1, 0);
            path.clear();
            over.clear();
            cnt = 0;

            // Calling DFS.
            dfs(x, -1, y);

            // Checking for unique values on the path.
            for (auto node : path)
            {
                  if (over[val[node]] > 0)
                        continue;
                  over[val[node]]++;
                  cnt++;
            }

            // Output of number of distinct values.
            cout << cnt << endl;
      }

      // Returning zero.
      return 0;
}

Input

8 2
105 2 9 3 8 5 7 7
1 2
1 3
1 4
3 5
3 6
3 7
4 8
2 5
7 8

Output

4
4

Complexity Analysis

Time Complexity

O(Q * N), where ‘Q’ is the number of queries and ‘N’ is the number of total nodes. 

Explanation: We are running DFS for every ‘Q’ query, and the time complexity for running DFS once is O(N) for N number of nodes. Thus the total time complexity is O(Q * N).

Auxiliary Space

O(N), where ‘N’ is the number of nodes.

Explanation: We are using an unordered map and a ‘vis’ vector occupying the linear space; thus, the auxiliary space is O(N).

FAQs

1. What is a tree?
   A Tree can be understood as a data structure that stores data in a hierarchical structure of nodes, having a root, edges, leaves, etc. 
    
2. How can we find the path between two nodes?
   To find the path between two nodes, we can use algorithms like BFS (Breadth-First Search) and DFS (Depth First Search) that are efficient and accurate concerning the requirements. 
    
3. What is DFS?
   DFS stands for Depth First Search, an algorithm used for traversing and exploring data structures like graphs and trees. It is considered the most efficient algorithm to traverse any graph or a tree.  
    
4. What is the time complexity of the above algorithm?
   The time complexity of the above algorithm is O(Q * N), where ‘Q’ is the number of queries and ‘N’ is the number of total nodes. 
    
5. What is the space complexity of the above algorithm?
   The space complexity of the above algorithm is O(N), where ‘N’ is the number of nodes as we are using an unordered map and a ‘vis’ vector occupying the linear space. 

Key Takeaways

The above problem is an interesting competitive programming problem involving DFS Algorithm. Solving these types of problems is the key to enhancing your knowledge of data structures and algorithms and boosting your problem-solving skills. 

Recommended Problems:

• Graph Valid Tree
• Multiplication Tree
• Largest BST In Binary Tree
   

Find more such interesting questions on our practice platform Coding Ninjas Studio if you want to learn more before jumping into practicing, head over to our library section for many such interesting blogs. Keep learning.

Happy Coding!