Naive Approach
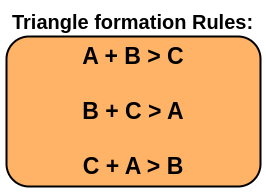
This approach is very simple to implement and straightforward. In this brute force method, three loops run and keep track of the number of triangles that can be formed thus far. Three different values are chosen from an array by the three loops. The innermost loop looks for the triangle property (the sum of any two sides of the triangle must be greater than the value of the third side of the triangle).
Let us see its algorithm.
Algorithm
Step 1: we will start with executing three nested loops, each beginning from the index of the previous loop and ending at the end of the array. for example, the first loop will run from 0 to n, the next loop j from i to n, and the next loop k from j to n.
Step 2: Then we will sort the array. And initialize the sum variable.
Step 3: Determine whether array[i] + array[j] > array[k], i.e. the sum of two sides is greater than the sum of the third.
Step 4: Increase the sum if all three conditions are met and print the sum value.
Let us see the implementation of this approach in the next section of this blog.
Also see, Rabin Karp Algorithm
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
int NumberOfTriangles(int arr1[], int n)
{
int sum = 0; // initialise count variable to count number of triangles
// These three loops select three different values from array
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
for (int k = j + 1; k < n; k++) // this loop checks for the triangle property
if (arr1[i] + arr1[j] > arr1[k] // triangle formation sum
&& arr1[i] + arr1[k] > arr1[j] && arr1[k] + arr1[j] > arr1[i])
sum++;
}
}
return sum;
}
int main()
{
int arr1[] = {2, 3, 4, 5, 6, 7};
int length = sizeof(arr1) / sizeof(arr1[0]);
cout << "Total number of possible triangles are: "
<< NumberOfTriangles(arr1, length);
return 0;
}

You can also try this code with Online C++ Compiler
Output
Total number of possible triangles are: 13
Let us analyze the time and complexity of this approach.
Time complexity
This approach will take O(n^3 ), where n is the size of the array. Because in this approach, we are using three loops, complexity will increase to n^3.
Space complexity
This will not cost any memory space. And it will take O(1).
Efficient solution
Another O(n2) time algorithm sorts the array but does not traverse the entire array in all three loops. In this approach, we will sort the array in ascending order first. Then employ two loops. The outer loop is used to fix the first side, the inner loop is used to fix the second side, and the third side is found by finding the farthest index of the third side (greater than the indices of both sides) whose length is less than the sum of the other two sides. So a range of values for the third side can be found where its length is guaranteed to be greater than the length of the other two individual sides but less than the sum of both sides.
Algorithm
Step 1: Sort the array in increasing order.
Step 2: Initialize
i = 0; // First Element
j = 1; // Second Element
count = 0; // Number of triangles
Step 3: WHILE (i<n-2)
k = j+1;
move k forward until arr[k] becomes > (arr[i] + arr[j]) or k moves out of bound
count = count + (k-j-1);
increment j
if j is at end of array
increment i and set j=i+1
Step 4: Print count.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
int compare(const void *a, const void *b)
{
return *(int *)a > *(int *)b;
}
int NumberOfTriangles(int array[], int n)
{
qsort(array, n, sizeof(array[0]), compare);
int count = 0;
for (int i = 0; i < n - 2; ++i)
{
for (int j = i + 1; j < n; ++j)
{
int k = j + 1;
while (k < n && array[i] + array[j] > array[k])
{
k = k + 1;
}
count = count + k - j - 1;
}
}
return count;
}
int main()
{
int n;
cout << "enter number of elements in the array: " << endl;
cin >> n;
cout << "enter array elements: " << endl;
int arr1[n];
for (int i = 0; i < n; i++)
{
cin >> arr1[i];
}
cout << "Total number of Triangles that can be formed are = " << NumberOfTriangles(arr1, n);
return 0;
}

You can also try this code with Online C++ Compiler
Output
enter number of elements in the array:
6
enter array elements:
2 3 4 5 6 7
Total number of Triangles that can be formed are = 13
Implementation in Java
import java.util.*;
public class NumberOfTriangles {
static int findNumberOfTriangles(int arr1[]) {
int n = arr1.length;
Arrays.sort(arr1);
int count = 0;
for (int i = 0; i < n - 2; ++i) {
// Initialize index of the rightmost third element
int k = i + 2;
for (int j = i + 1; j < n; ++j) {
while (k < n && arr1[i] + arr1[j] > arr1[k])
++k;
if (k > j)
count += k - j - 1;
}
}
return count;
}
public static void main(String[] args) {
int arr1[] = { 2, 3, 4, 5, 6, 7 };
System.out.println("Total number of possible triangles is " + findNumberOfTriangles(arr1));
}
}

You can also try this code with Online Java Compiler
Output
Total number of possible triangles is: 13
Now let us analyze the time and complexity of the above approach.
Time complexity
The time complexity of this algorithm is O(n^2) where n is the number of elements. The time complexity appears to be increased as a result of three nested loops. In the outermost loop, k is only initialized once. Because k starts from i+2 and rises to n for all values of j, the innermost loop executes in at most O(n) time for each iteration of the outermost loop. Thus, the time complexity is O(n^2).
Space complexity
The space complexity is O(1).
Check out this problem - Two Sum Problem
Frequently Asked Questions
What is the Array's default value?
Any new Array is always initialized with the following default value: The default value for byte, short, int, and long is zero (0). For float and double the default value is '0.0'. For Boolean the default value is false, and for the object the default value is null.
What exactly is a Sparse Array?
A sparse array is a data array that contains many elements with zero values. A dense array, on the other hand, has the majority of its elements with non-zero values. Sparse arrays map integers to objects and can have gaps in their indices.
In Java, how do you convert an array to a tree set?
To convert an array to a tree set in Java, first convert the array to a list using the asList() method of the Arrays class and then pass the list object to the TreeSet constructor
Conclusion
To conclude this blog, firstly we discussed the problem statement and different ways to solve the problems. For the first approach, we discussed its algorithm, pseudo-code, and complexities. And then we discussed another approach. We eventually saw how both the ways are different from each other.
Refer to our guided paths on Coding Ninjas Studio to upskill yourself in Data Structures and Algorithms, Competitive Programming, JavaScript, System Design, and many more! If you want to test your competency in coding, you may check out the mock test series and participate in the contests hosted on Coding Ninjas Studio! But if you have just started your learning process and looking for questions asked by tech giants like Amazon, Microsoft, Uber, etc; you must have a look at the problems, interview experiences, and interview bundle for placement preparations.
Nevertheless, you may consider our paid courses to give your career an edge over others!
Do upvote our blogs if you find them helpful and engaging!
Happy Learning!