Introduction
This article will look at the problem of counting triplets with a sum smaller than a given value. Array-based questions are the most popular and vital in coding interviews and programming competitions. Let's understand the problem statement.
Problem Statement
We are given an array arr[] of different integers of size N and a value sum. The goal is to print the count of triplets (i, j, k) with the sum of triplets (arr[i] + arr[j] + arr[k]) smaller than the given value sum.
Sample Examples
Example 1:
Input 1:
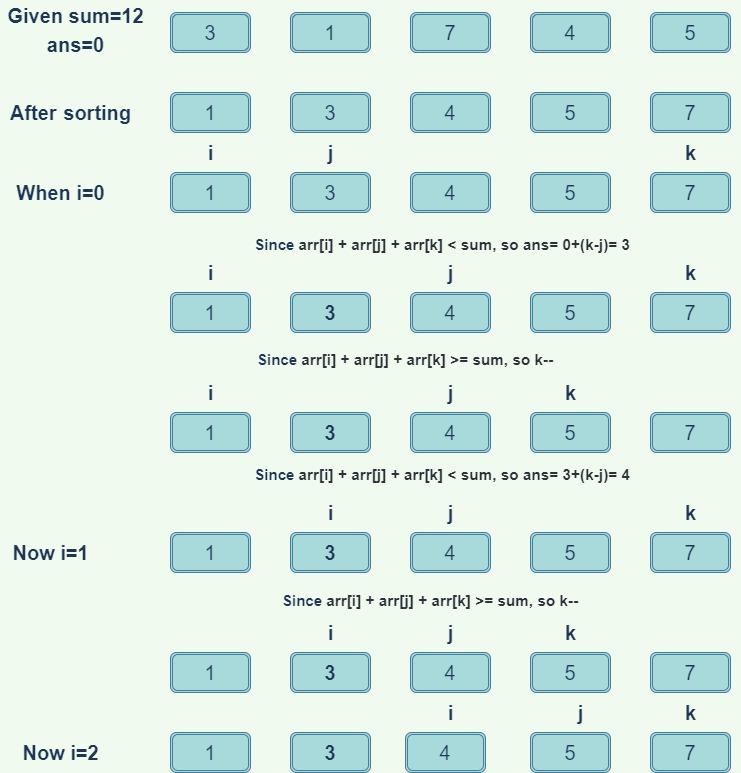
N=5, sum= 12, arr[] = { 3, 1, 7, 4, 5}
Output 1:
4
Explanation: Below are triplets with a sum less than 12 (3, 1, 4), (3, 1, 5), (3, 1, 7), and (1, 4, 5).
Example 2:
Input 2:
N = 4, sum = 2, arr[] = {0, -2, 1, 3}
Output 2:
2
Explanation: The triplets with sum less than 2 are (0, -2, 1) and (0, -2, 3).
Also see, kth largest element in an array, and Euclid GCD Algorithm
Brute Force approach
In this method, we will run three loops to consider all triplets one by one. For every triplet, compare the sums and increment count if the triplet sum is smaller than the given sum.
Steps of Algorithm
- Initialize the answer count as 0.
- Run the first loop from i=0 to less than (length-2) to get the first triplet.
- Run the second loop from j=i+1 to less than (length-1) to get the second triplet.
- To get the third triplet, run a loop from k=j+1 to less than (length).
- Add these triplets and check the condition if the sum is less than the required sum.
- Increment the count if condition satisfies.
- End the loop.
Implementation
Code In Java:
import java.util.Arrays;
class Test
{
static int arr[] = new int[]{3, 4, 7, 5, 1};
static int countTriplets(int n, int sum)
{
int ans = 0;
for (int i = 0; i < n-2; i++)
{
for (int j = i+1; j < n-1; j++)
{
for (int k = j+1; k < n; k++)
if (arr[i] + arr[j] + arr[k] < sum)
ans++;
}
}
return ans;
}
// driver method
public static void main(String[] args)
{
int sum = 12;
System.out.println(countTriplets(arr.length, sum));
}
}
Code In C++:
#include<bits/stdc++.h>
#include<bits/stdc++.h>
using namespace std;
int countTriplets(int arr[], int n, int sum)
{
int ans = 0;
for (int i = 0; i < n-2; i++)
{
for (int j = i+1; j < n-1; j++)
{
for (int k = j+1; k < n; k++)
if (arr[i] + arr[j] + arr[k] < sum)
ans++;
}
}
return ans;
}
// Driver program
int main()
{
int arr[] = {3, 4, 7, 5, 1};
int n = sizeof arr / sizeof arr[0];
int sum = 12;
cout << countTriplets(arr, n, sum) << endl;
return 0;
}
Output:
4
Complexity Analysis
Time complexity: O(n^3) because of three nested loop
Space Complexity: O(1), we cannot use any extra memory