Problem Statement
The problem states that we need to find a number of ways to draw N non-intersecting chords in a circle using 2N points.
Let us try to understand the problem better with some examples. Suppose you are given N=2. That means you have 2*2 = 4 points. So there could be two ways in which you could draw N non-intersecting chords within the circle.
See the figure above. We were given N=2. So we had 4 points to work within the circle, and our task was to find out the number of ways to draw N non-intersecting chords. Identifying the above 2 figures are all the possible ways to do so.
The problem statement could also be viewed as the number of all possible ways of dividing the circle using N non-intersecting chords.
Solution Approach
Suppose there are 8 points on a circle. If we connect any of the two points in the circle, it divides the points into two sets of points that can’t be connected because then they wouldn’t be non-intersecting chords. Let us take a look at the illustration given below for a better understanding.
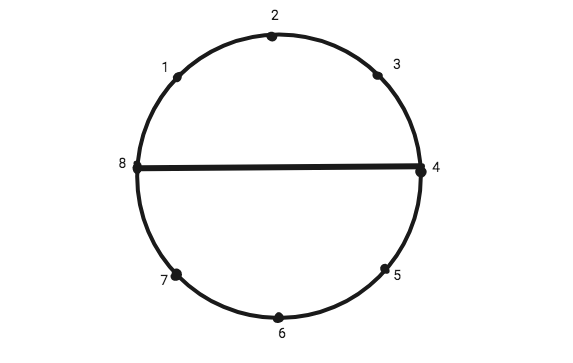
Here we connected points 4 and 8. This divided the points into 2 smaller sets i.e {1,2,3} and {5,6,7}. Now note that no two points from different sets can be used to draw a chord. If we do, the chord will intersect the line we just drew.
This way, we devise a recurrence relation to the above problem.
WAYS(N) = SUM( i = 0 to N-1) {WAYS(N) * WAYS(N-i-1)}
Here we iterate over i, assuming that the size of one of the sets is i and the size of another set automatically is (N-i-1) since we’ve already used a pair of points and i pair of points in one set.




