Example of Cyclomatic Complexity
Consider the following simple function in pseudo-code:
function example(a, b):
if a > 0:
if b > 0:
print("Both a and b are positive")
else:
print("a is positive, but b is not")
else:
print("a is not positive")
Here is a breakdown of the control flow:
- Start at the function entry.
- Check the condition if a > 0.
- If true, check the nested condition if b > 0.
- If true, print "Both a and b are positive".
- If false, print "a is positive, but b is not".
- If false, print "a is not positive".
The control flow graph for this function would have:
- 4 nodes (representing decisions and end points)
- 5 edges (representing the transitions between these nodes)
Formula for Calculating Cyclomatic Complexity
The formula to calculate cyclomatic complexity (V(G)) is:
V(G)=E−N+2P
Where:
- E= the number of edges in the control flow graph
- N= the number of nodes in the control flow graph
- P = the number of connected components (usually 1 for a single program)
Using the example function, we have:
- E=5(edges)
- N=4(nodes)
- P=1(connected components)
Applying the formula:
V(G)=5−4+2×1
V(G)=5−4+2
V(G)=3
So, the cyclomatic complexity of the example function is 3.
This means there are 3 independent paths through the function, indicating the number of test cases needed to achieve complete branch coverage.
Calculation of Cyclomatic Complexity
The steps that should be followed for calculating the cyclomatic complexity and test cases design are mentioned below:
- Constructing graph with edges and nodes from the code
- Identifying the independent paths
- Calculating the cyclomatic complexity
- Designing the test cases
There are various methods of calculating the cyclomatic complexity of a program. Some of them are discussed below.
Method 1:
In mathematical terms, the cyclomatic complexity of a control flow graph G, V(G) can be calculated using the formula given below.
V(G) = E - N + 2*P
where
E is the number of edges in the control flow graph,
N is the number of nodes in the control flow graph, and
P is the number of connected components (exit points).
Method 2:
Cyclomatic complexity can also be calculated by
V(G) = P + 1
where
P is the number of predicate nodes (nodes containing conditions).
Method 3:
Cyclomatic complexity is the number of regions in a control flow graph.
Let us take an example to understand the calculation of cyclomatic complexity.
Let us consider the following snippet of code.
a = 15 ;
if ( a > b ) then
a = b ;
else
{
if ( a > c ) then
b = c ;
else
c = a ;
end if;
}
end if;
print a
print b
print c
Let us construct the control flow graph now.
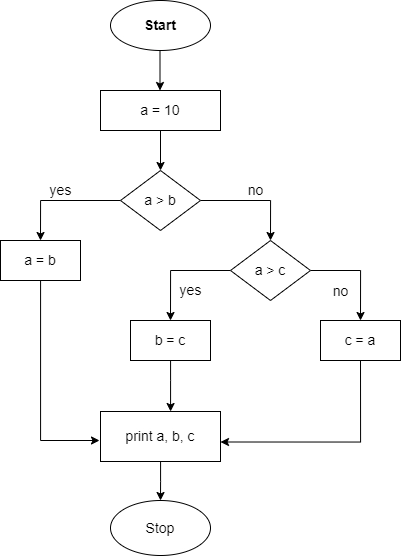
Using method 1: E = 10, N = 9, P = 1
Hence, V(G) = E - N + 2*P = 10 - 9 + 2 * 1
V(G) = 3
Using method 2: P = 2
Hence, V(G) = P + 1 = 2 + 1
V(G) = 3
Using method 3: Number of regions in control flow graph = 3
Hence, V(G) = 3
Also read V Model in Software Engineering
Properties of Cyclomatic Complexity
Subsequent are the properties of cyclomatic complexity:
- It represents the maximum number of independent paths in the control flow graph.
- It is always greater than or equal to zero.
- Insertion or deletion of functional statements from the code does not affect its cyclomatic complexity.
- Programs with lower complexity numbers are easier to interpret and less risky to modify.
- If the complexity number is high, then the error probability increases along with the time taken for troubleshooting and maintenance.
The upper bound of cyclomatic complexity is the number of test cases required to achieve branch coverage, whereas the lower bound is the number of paths through the graph.
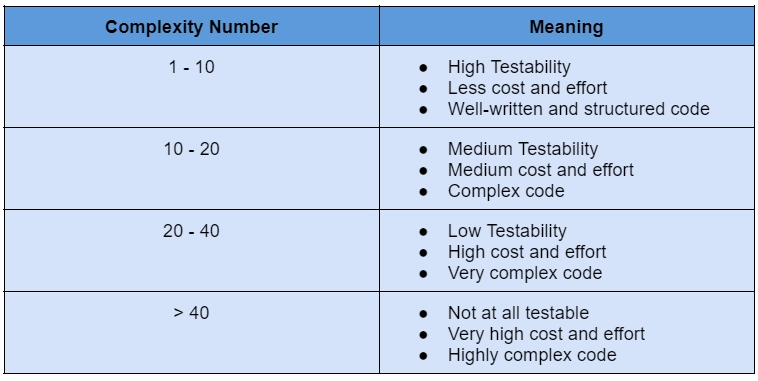
The table below gives a brief description of the complexity number and its meaning of cyclomatic complexity.
Uses of Cyclomatic Complexity
Some of the notable uses of cyclomatic complexity are mentioned below.
- The determination of independent path executions has proved to be very helpful for Developers and Testers.
- Testing of each path is made sure to be done at least once.
- Code coverage can be improved in Software Engineering.
- It helps in focusing more on the uncovered paths.
- It evaluates the risks associated with the program.
- When used earlier in the program, it helps in risk reduction.
Advantages of Cyclomatic Complexity
As we have already observed that cyclomatic complexity is a very useful tool, here are some of the advantages that give it an edge over others.
- It gives the relative complexity of various designs and hence can be used as a quality measure.
- It is used to measure the best areas of concentration and minimum efforts for testing.
- It computes faster than Halstead’s metrics.
- Its application is easy.
- It guides the process of testing.
Disadvantages of Cyclomatic Complexity
With pros come cons, thus the cons of cyclomatic complexity are stated as follows:
- It is not the measure of the program's data complexity but only the control complexity.
- For simple comparison and decision structures, it may give a deceiving value.
- In Cyclomatic Complexity, nested conditional structures are harder to understand when compared to non-nested ones.
Frequently Asked Questions
What is a cyclomatic complexity of 8?
A cyclomatic complexity of 8 indicates a function with 8 independent paths, suggesting higher complexity and potential difficulty in understanding and testing.
What is a good cyclomatic complexity?
A good cyclomatic complexity is typically 10 or less, as this indicates manageable code that is easier to understand, test, and maintain.
What is the rule of cyclomatic complexity?
The rule of cyclomatic complexity is to keep it low, ideally under 10, to ensure code is understandable, maintainable, and easier to test.
What is cyclomatic complexity in black box testing?
Cyclomatic complexity is not directly used in black box testing; it is a metric for white box testing, measuring internal code complexity.
Name some tools used for calculating Cyclomatic Complexity.
Many tools are available to find the complexity of an application. Some of these are technology-specific.
- GMetrics: discovers metrics in Java-related applications
- OCLint: Static code analyzer for C and related languages
Conclusion
In this article, we acquired knowledge about cyclomatic complexity. We also learned how to calculate it; its properties, uses, advantages and disadvantages.
As we know, there are various ways to measure the quality of a program or algorithm; you can visit these sensational articles on Time Complexity and Space Complexity.
Happy Reading!








