Dec 2015 Paper-II - Part-1

Introduction

The UGC NET JRF Computer Science is a great way to start your career as a Computer Science Lecturer. The UGC's NET exams provide an opportunity to begin a career as a lecturer in colleges, universities, and other educational institutions. The tests are held twice a year.  

Note: This article contains Q.No. 1 to Q.No. 25 out of the 50 questions asked in UGC NET Dec 2015 paper II. The solutions to Q.No. 26 to Q.No. 50 can be found in the UGC NET Dec 2015 Paper-II Part-2 article.

 

Question 1: How many five-person committees can be formed from a pool of 20 men and 12 women, with at least three women on each committee?

1. 75240
2. 41800
3. 52492
4. 9900

Answer:- C

Explanation:-

We must choose at least three ladies, therefore we compute the cases of three women, four women, and five women, then sum the results using the addition method.

¹²C₃ x ²⁰C₂ + ¹²C₄ x ²⁰C₁ + ¹²C₅ x ²⁰C₀ = ((12x11x10)/(3x2x1)) x (20x19/2x1)

                                                     + (12x11x10x9/4x3x2x1) x 20

                                                     + (12x11x10x9x8/5x4x3x2x1) x 1

                                                  = 220 x 190 + 495 x 20 + 792

                                                  = 52492

 

Question 2: Which one (or more) of the following statements is/are false?

1. A connected multigraph has an even degree if each vertex has an Euler circuit.
2. If it contains exactly two vertices of odd degree, a linked multigraph does not have an Euler circuit but has an Euler Path.
3. When n3 is 3, a Hamilton Circuit exists in a complete graph (Kn).
4. A six-vertice cycle (C6) is not a bipartite graph, but a complete graph with three vertices is.

 

1. 1 only
2. 2 and 3
3. 3 only
4. 4 only

Answer: D

Explanation:

A graph's Euler circuit G is a simple circuit that includes all G's edges.

A connected multigraph has an even degree if each vertex has an Euler circuit.

A Hamilton Path is a graph path that passes through each vertex exactly once. A Hamilton Circuit is a Hamilton path with the same vertex at both ends.

From the above statements, we see that option D is false. Hence it is the correct answer.

 

Question 3: Which of the following is/are not true?

1. The collection of non-positive numbers is countable.
2. It is possible to count the number of numbers multiples of 7.
3. Even integers can be counted as a set.
4. The real numbers between 0 and 1/2 are countable.

 

1. 1 and 3
2. 2 and 4
3. 2 only
4. 4 only

Answer: D

Explanation:

There are infinite real numbers between any two real numbers. Hence it is impossible to write it on set and impossible to count. Hence option D is false. Hence it's the correct answer.

 

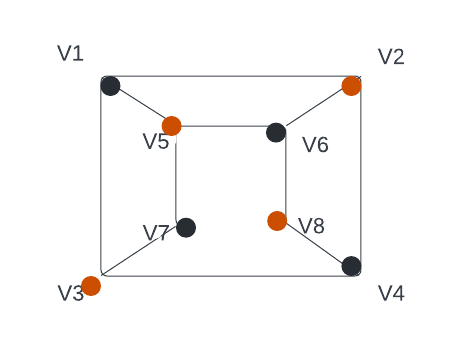
Question 4: Given below is a graph:

Given below is the two distinct sets of vertices, which make the graph bipartite are:

1. (v1, v4, v6); (v2, v3, v5, v7, v8)  
2. (v1, v7, v8); (v2, v3, v5, v6)
3. (v1, v4, v6, v7); (v2, v3, v5, v8) 
4. (v1, v4, v6, v7, v8); (v2, v3, v5)

Answer: C

Explanation:

If the vertex set of a simple graph G=(V, E) can be partitioned into two disjoint subsets V=V1V2, and every edge has the form e=(a,b), where aɛV1 and bɛV2.

Two-colorable graphs are equivalent to bipartite graphs.

 

1. Change the colour of the source vertex to Red (putting into set V1).
2. Use black to colour in all of your neighbours (putting into set V2).
3. Use red to colour all of your neighbours' neighbours (putting into set V1).
4. Assign colour to all vertices in this fashion so that it satisfies all of the requirements of the m-way colouring problem, where m = 2.
5. If we find a neighbour with the same colour as the current vertex while assigning colours, the graph cannot be coloured with two colours (ie., graph is not Bipartite).

As a result, the solution is option (C).

 

Question 5: If the absolute value of the difference of the labels of neighbouring vertices is all different, a tree with n vertices is said to be elegant if its vertices may be labelled with integers 1, 2,...,n. Which of the following trees has the most graceful branches?

 

1. 1 and 2
2. 2 and 3
3. 1 and 3
4. 1, 2 and 3

Answer: D

Explanation:

 

 

Question 6: Which of the following is not a valid argument?

1. "Gora will be promoted if he obtains the job and works hard. Gora will be pleased if he receives a promotion. He won't be happy; therefore, he won't get the job or put in the effort".
2. “Puneet is either innocent or Pankaj is telling the truth. Puneet is not guilty since Pankaj is not telling the truth.”.
3. If n is a real number greater than one, then n2 is more than one. If n2>1, then n>1 is true.

 

1. 1 and 3
2. 2 and 3
3. 1, 2 and 3
4. 1 and 2

Answer: C

Explanation:

All the provided arguments are not valid.

 

Question 7: Let the P(m,n) be the assertion "m divides n," with the set of integers greater than zero as the Universe of Discourse for both variables. The truth values of the following assertions must be determined.

1. Ǝm ∀n P(m,n) (b) ∀n P(1,n) (c) ∀m∀n P(m,n)
2. ∃m ∀n P(m,n)
3. ∀n P(1,n) 
4. ∀n P(1,n) m∀n P(1,n) nP(m,n)

Answer: A

Given P(m,n) = "m divides n"

Statement-A is Ǝm ∀n P(m, n). Here, there exists some positive integer that divides every positive integer. It is true because there is a positive integer 1 which divides every positive integer

Statement-B is ∀n P(1, n). Here, 1 is divided every positive integer. It is true.

Statement-C is ∀m ∀n P(m, n). Here, every positive integer divided every positive integer. It is false.

 

Question 8: Match the following:

S.No	List - 1	List - 2
1.	Vacuous proof	(i) The fact that p is untrue is used to prove that the implication p---->q is true.
2.	Trivial Proof	(ii) Based on the knowledge that q is true, a proof that the implication p —> q is true.
3.	(c ) Direct Proof	(iii) A proof that the implication p→q is true that proceeds by showing that q must be true when p is true.
4.	(d) Indirect Proof	(iv) A proof that the implication p→q is true that proceeds by showing that p must be false when q is false.

 

       (a)  (b)   (c)    (d)

(A)   (i)   (ii)   (iii)   (iv)

(B)   (ii)   (iii)   (i)   (iv)

(C)   (iii)   (ii)   (iv)  (i)

(D)   (iv)   (iii)   (ii)  (i)

Answer: A

Explanations:

• Vacuous proof is a proof in which the implication p → q is true based on the fact that p is false.
• Trivial proof is a proof in which the implication p → q is true based on the fact that q is true.
• Direct proof is A proof in which the implication p → q is true that proceeds by showing that q must be true when p is true.
• Indirect proof a proof in which the implication p → q is true that proceeds by showing that p must be false when q is false.

So, option (A) is correct.

 

Question 9: Consider the compound propositions given below as:

1. pv~(p^q) 2.    (p˄~q)˅~(p˄q) 3.   p˄(q˅r) 

Which of the above propositions are tautologies?

1. 1 and 3
2. 2 and 3
3. 1 and 2
4. 1 only

Answer: D

Explanation:

p ∨ ~(p ∧ q) = p + (pq)` = p + p` + q` = 1 + q` = 1. It’s a tautology.

(p ∧ ~q) ∨ ~(p ∧ q) = pq` + (pq)` = pq` + p` + q` = p` + q`. It’s not a tautology.

p ∧ (q ∨ r) = pq + pr. It’s not a tautology.

So, option (D) is correct.

 

Question 10: To be an Abelian group, a Group G must possess which of the following properties?

1. The distributive property
2. The commutative property
3. The symmetric property

 

1. 1 and 2
2. 2 and 3
3. 1 only
4. 2 only

Answer: (D) 2 only

Explanation:

To be an Abelian group, the commutative property must hold. Because the group is specified, all other properties are included.

 

Question 11: Consider the following program:

#include<stdio.h>

main()

{

int i, inp;

float x, term=1, sum=0;

scanf(“%d %f”,&inp, &x);

for(i=1;i<=inp;i++)

{

             term=term*x/i;

             sum=sum+term;

}

printf(“Result=%f\n”,sum);

}

The program computes the sum of which of the following series?

1. x+x2/2+x3/3+x4/4+... 
2. x+x2/2!+x3/3!+x4/4!+...
3. 1+x2/2+x3/3+x4/4+...
4. 1+x2/2!+x3/3!+x4/4!+...

Solution: (B) x+x2/2!+x3/3!+x4/4!+...

Explanation:

Let, i=1, term=1, term=1*x/1, sum=0+(x/1)

i=2, term=x  , term =x*x/2, sum=x+x²/2

i=3 term=x²/2 , term =x³/6, sum =x+x²/2+x³/6

And do the same further you will get,

x+x2/2!+x3/3!+x4/4!+...

 

Question 12: Consider the following two statements:

(a) A publicly derived class is a subtype of its base class.

(b) Inheritance provides for code reuse.

Which of the following statements is correct?

1. Both the statements (a) and (b) are correct
2. Neither of the statements (a) and (b) are correct
3. Statement (a) is correct and (b) is incorrect
4. Statement (a) is incorrect and (b) is correct

Solution: (A) Both the statements (a) and (b) are correct

Explanation:

• A subtype of its base class is a publicly derived class.
• Inheritance allows code to be reused.

So, answer A is correct.

 

Question 13: Consider a “CUSTOMERS” database table having a column “CITY” filled with all the names of Indian cities (in capital letters). The SQL statement that finds all cities that have “GAR” somewhere in its name, is:

1. Select *from customers where city=’%GAR%’;
2. Select *from customers where city=’$GAR$’;
3. Select *from customers where city like ‘%GAR%’;
4. Select *from customers where city as ’%GAR’;

Solution: (C) Select *from customers where city like ‘%GAR%’;

Explanation:

In above question a specific pattern "GAR" is given for pattern matching

In SQL "LIKE" clause is used for pattern matching. For LIKE clause we have two wild cards:

1. "%" which represents any sequence of "o" or more characters.

2."_"is used to replace a single character.

So, Option C is the correct answer because they have used LIKE clause along with "9%" which indicates any number of character can be present

before and after "GAR" pattern.

 

Question 14: Match the following database terms to their functions:
 

	LIST-I	LIST-II
(a)	Normalization	(i) Enforces match of primary key to foreign key
(b)	Data Dictionary	(ii) Reduces data redundancy in a database
(c)	Referential Integrity	(iii) Define view(s) of the database for particular user(s).
(d)	External Schema	(iv) Contains metadata describing database structure.

 

Codes:  (a)   (b)    (c)   (d)

1.  (iv)    (iii)   (i)   (ii)
2.  (ii)    (iv)   (i)   (iii)
3.  (ii)   (iv)   (iii)   (i)
4.  (iv)   (iii)   (ii)   (i)

Solution: (B)

Explanation:

• Normalisation reduces data redundancy in a database
• Data Dictionary contains metadata describing database structure defines view(s) of the database for particular user(s)
• Referential Integrity enforces match of primary key to foreign key
• External Schema defines view(s) of the database for particular user(s)

So, option (B) is correct.

 

Question 15: In general, in a recursive and non-recursive implementation of a problem (program):

1. Both time and space complexities are better in recursive than in non-recursive program
2. Both time and space complexities are better in non-recursive than in recursive program
3. Time complexity is better in recursive version but space complexity is better in non-recursive version of the program
4. Space complexity is better in recursive version but time complexity is better in non-recursive version of the program

Solution: (B) Both time and space complexities are better in non-recursive than in recursive program

Explanation:

In general, both time and space complexity in a recursive and non-recursive implementation of a problem (program) are better in the non-recursive program than in the recursive program. The recursive implementation also offers the worst-case situation in some programs. As a result, a recursive implementation may not always ensure the best situation.

As a result, option (B) is correct.

 

Question 16: A three dimensional array ‘C’ is declared as int A[x][y][z]. Consider that array elements are stored in row-major order and indexing begins from 0. Here, the address of an item at the location A[p][q][r] can be computed as follows (where w is the word length of an integer):

1. &A[0][0][0] + w(y * z * q + z * p + r)
2. &A[0][0][0] + w(y * z * p + z*q + r)
3. &A[0][0][0] + w(x * y * p + z * q+ r)
4. &A[0][0][0] + w(x * y * q + z * p + r)

Solution: (B) =  &A[0][0][0] + w(y * z * p + z*q + r)

Explanation:

According to the query, we must locate address A [p] [q] [r]

We must cross 0 to p-1 row, i.e. p rows,  and each row includes y*z components.

As a result

= y*z*p

Now we must cross q rows to get to the q^th element in the p^th row, and each row has z(total columns) elements = z∗q

We must cross r elements in the (p+1)^th row to get to the r^th elements. = (y*z*p+z*q+r)

Each element now takes up m bytes of memory space.

As a result, the total space used by these items equals m(y*z*p+z*q+r).

As a result, A[p][q][r]=base address+ the Elements that had occupied the space.

=&A[0][0][0] + m(y*z*p+z*q+r)

As a result, Option (B) is right.

 

Question 17: In C++, which system-provided function is called when no handler is provided to deal with an exception?

1. terminate()
2. unexpected()
3. abort()
4. kill()

Solution (A) terminate 

Explanation:

terminate() is the system-provided function which is called when no handler is provided to deal with an exception.

 

Question 18: Which of the following provides the best description of an entity type?

1. A specific concrete object with a defined set of processes (e.g. Jatin with diabetes)
2. A value given to a particular attribute (e.g. height-230 cm)
3. A thing that we wish to collect data about zero or more, possibly real world examples of it may exist.
4. A template for a group of things with the same set of characteristics that may exist in the real world.

Solution: (D) A template for a group of things with the same set of characteristics that may exist in the real world

Explanation:

It is a group of entities that have a common attribute. Each row in the Student table is an object with shared properties.

As a result, STUDENT is an entity type that includes entities with the characteristics id, name, and age. In addition, each database entity type has a name and a set of attributes.

As a result, we can classify a table as an entity type.

The following information is included in each template:

• A distinctive moniker. (Required.)
• One or more properties define an entity key. (Required.)
• The information is in the form of properties (Optional.)
• The navigation characteristics allow you to move from one end of an association to the other. (Optional)

 

Question 19: Data which improves the performance and accessibility of the database are called:

1. Indexes
2. User Data
3. Application Metadata
4. Data Dictionary

Solution: (A) Indexes

Explanation:

Indexes are data that improve the database's performance and accessibility. An index is a type of data that improves the lookup table. Simply said, an index is a pointer to data in a table that improves accessibility in a book or database. With the help of an index, we may quickly retrieve any information.

 

Question 20: A relation R={A,B,C,D,E,F,G} is given with following set of functional dependencies:

F={AD→E, BE→F, B→C, AF→G}

Which of the following is a candidate key?

1. A
2. AB
3. ABC
4. ABD

Solution: (D) 

Explanation:

Nothing drives all of the characteristics, but if we add B to the first key, [ADB], it will return all of them [ADB]+ = ABCDEFG.

[AD]+ = ADE.

[BE]+ = BCEF.

[B]+ = BC.

[AF]+ = AFG.

Hence, option (D) is correct.

 

Question 21: Which of the following services is not provided by wireless access point in 802.11 WLAN?

1. Association
2. Disassociation
3. Error Correction
4. Integration

Solution: (C) Error Correction

Explanation:

In an 802.11 WLAN, the wireless access point provides the following services:

Integration

Disassociation

Association

We have distinct policies for error correction, and wireless access points in 802.11 WLAN do not give correction.

As a result, option (C) is the correct answer.

 

Question 22: Which of the following fields in IPV4 datagram is not related to fragmentation?

1. Type of service
2. Fragment offset
3. Flags
4. Identification

Solution: (A) Type of Service

Explanation:

The type of service has nothing to do with IPV4 datagrams. IPV4 datagram is associated with flags, identity, and fragmentation offset.

As a result, option (A) is the correct answer.

 

Question 23: Four channels are multiplexed using TDM. If each channel sends 100 bytes/second and we multiplex 1 byte per channel, then the bit rate for the link is __________.

1. 400 bps
2. 800 bps
3. 1600 bps
4. 3200 bps

Solution: (D) 3200

Explanation: 

Number of channels = 4

1 byte is multiplexed with each channel i.e. each frame carries 1 byte and we have 4 channels, so the size of each frame is 1 * 4 byte = 4 bytes or 32 bits.

Channel sends 100 frames per second. So, the bit rate will be 100 * 4 bytes i.e. 3200 bits/seconds.

 

Image: Multiplexer

 

So, option (D) is correct.

 

Question 24: In a typical mobile phone system with hexagonal cells, it is forbidden to reuse a frequency band in adjacent cells. If 840 frequencies are available, how many can be used in a given cell?

1. 280
2. 110
3. 140
4. 120

Solution: (A) 280

Explanation:

In a hexagonal grid, each cell is surrounded by six other cells. If the central cell utilises frequency group A, the six neighbouring cells can use B, C, B, C, B, and C respectively. In other words, only three distinct cells are required. So, 840/3 = 280 frequencies is the answer.

 

Question 25: Using p = 3, q = 13, d = 7 and e = 3 in the RSA algorithm, what is the value of ciphertext for a plain text 5 ?

1. 8
2. 16
3. 26
4. 33

Solution: (A) 8

Explanation:

p=3, q=13, d=7, e=3, M=5, C=?

C=Me mod n

n = p*q

   = 3*13

   = 39

C = 53 mod 39

    = 8

Answer to this question is 8. 

 

FAQs

Who can apply for UGC NET computer science?

Candidates who have received at least 55 percent (without rounding off) in a Master's Degree OR equivalent examination in Humanities (including languages), Social Science, Computer Science & Applications, Electronic Science, etc. from universities/ institutions recognized by the UGC are eligible for this exam.

What is UGC NET for computer science?

Computer science encompasses a wide range of topics, including computer applications, programming, databases, computer networks, operating system software, experimentation, communication, computation, and the design of computational systems, among others.

How many papers are there for UGC NET computer science?

2 Papers

In Paper-1 and Paper-2, a total of 50 questions and 100 questions are asked respectively; each carrying 2 marks.

What is the pass mark in UGC NET?

Candidates who have passed the UGC NET with the required minimum qualifying marks, i.e. 40% for General and 35% for Reserved Category, will be declared.

Can we give 2 subjects on the net?

No, in the UGC NET, you cannot write two subjects at the same time. You can only concentrate on one issue at a time. You must have a master's degree in your discipline to apply for the UGC NET.