Introduction
The UGC NET, also known as the NTA-UGC-NET, is an examination used to determine eligibility for assistant professorships and Junior Research Fellowships at Indian universities and colleges. The National Testing Agency administers the exam on behalf of the University Grants Commission.
Now we will look at some of the questions that came in UGC NET Dec 2018 Paper II. Also check Dec 2018 Paper II - Part 1, Dec 2018 Paper II - Part 3, and Dec 2018 Paper II - Part 4 here.
Questions with Solutions
26. A binary search tree is constructed by inserting the following numbers in order:
60, 25, 72, 15, 30, 68, 101, 13, 18, 47, 70, 34
The number of nodes in the left subtree is
(1) 5
(2) 6
(3) 7
(4) 3
Solution) 7
Explanation) Given that it is a Binary search tree, it is important to notice that it is not balanced.
So, the first insertion element is ROOT, and all elements smaller than ROOT are found in the left subtree of ROOT.
60,25,72,15,30,68,101,13,18,47,70,34,
∴ in the inserting elements 25,15,30,13,18,47,34 are less than 60 and 72,68,101,70 are grater than 60.
Number of nodes in ROOT's left subtree = number of nodes below ROOT = 7.
27. Match List-I with List-II and choose the correct answer from the code given below:
List I (Graph Algorithm) List II (Time Complexity)
(a) Dijkstra’s algorithm (i) O(E lg E)
(b) Kruskal’s algorithm (ii) Θ(V3)
(c) Floyd-Warshall algorithm (iii) O(V2)
(d) Topological sorting (iv) Θ(V+E)
where V and E are the number of vertices and edges in graph respectively.
Code:
(1) (a)-(i), (b)-(iii), (c)-(ii), (d)-(iv)
(2) (a)-(iii), (b)-(i), (c)-(ii), (d)-(iv)
(3) (a)-(i), (b)-(iii), (c)-(iv), (d)-(ii)
(4) (a)-(iii), (b)-(i), (c)-(iv), (d)-(ii)
Solution) (a)-(iii), (b)-(i), (c)-(ii), (d)-(iv)
Explanation) Computer science has a concept called time complexity which deals with quantifying the amount of time taken by a snippet of code or algorithm to run as a function of the amount of input. So the answer to this question is -
(a) Dijkstra’s algorithm (iii) O(V2)
(b) Kruskal’s algorithm (i) O(E lg E)
(c) Floyd-Warshall algorithm (ii) Θ(V3)
(d) Topological sorting (iv) Θ(V+E)
28. In K-coloring of an undirected graph G=(V,E) is a function. c:V→{0,1,…,K−1} such that c(u)≠c(v) for every edge (u,v)∈E.
Which of the following is not correct?
(1) G is bipartite
(2) G is 2-colorable
(3) G has cycles of odd length
(4) G has no cycles of odd length
Solution) G has cycles of odd length
Explanation) A bipartite graph is a special kind of graph with the following properties-
- The vertices of set X join only with the vertices of set Y.
- It consists of two sets of vertices X and Y.
- The vertices within the same set do not join.
Bipartite graphs may be characterised in several different ways:
A graph is bipartite if and only if it does not contain an odd cycle.
A graph is bipartite if and only if it is 2-colorable, (i.e. its chromatic number is less than or equal to 2).
The spectrum of a graph is symmetric if and only if it’s a bipartite graph.
29. Consider a singly linked list. What is the worst case time complexity of the best-known algorithm to delete the node a, pointer to this node is q, from the list?
(1) O(n lg n)
(2) O(n)
(3) O(lg n)
(4) O(1)
Solution) O(n)
Explanation) Let X represent the Node that needs to be deleted.
We only have the next pointer in a single linked list, but no previous pointer.
However, we must first locate the prior node to X ==>, which takes O(n) in the worst scenario.
q-> next = previous -> next;
(q) ; (q) ; (q) ; (q)
it merely takes O(1) time.
O(1) = O(n) = O(n) = O(n) = O(n) = O(n) = O(n (n).
30. The second smallest of n elements can be found with ............... comparisons in the worst case.
(1) n−1
(2) lg n
(3) n+ceil(lg n) - 2
(4) 3n/2
Solution) n+ceil(lg n) - 2
Explanation)


31. Let r = a(a + b)*, s = aa*b and t = a*b be three regular expressions.
Consider the following:
(i) L(s) ⊆ L(r) and L(s) ⊆ L(t)
(ii) L(r) ⊆ L(s) and L(s) ⊆ L(t)
Choose the correct answer from the code given below:
Code:
(1) Only (i) is correct
(2) Only (ii) is correct
(3) Both (i) and (ii) are correct
(4) Neither (i) nor (ii) is correct
Solution) Only (i) is correct
Explanation)

32. Consider the language L given by
L = {2nk ∣ k>0, and n is non-negative integer number}
The minimum number of states of finite automaton which accepts the language L is
(1) n
(2) n+1
(3) n(n+1)/2
(4) 2n
Solution) n+1
Explanation)
For n=2, {22k | k>0} = {22, 24, 26, ...... }, the automata will look like -
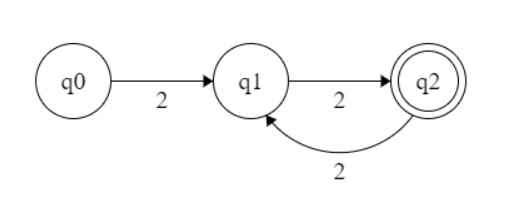
For n=3, {23k | k>0} = {23, 26, 29, ...... }, the automata will look like -
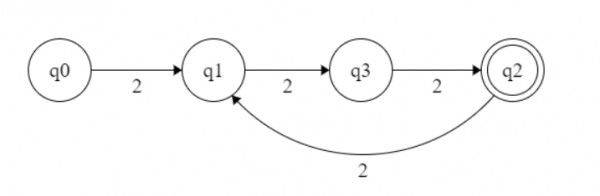
Note- We saw that the states are n+1 for {2nk | k>0}.
33. The number of substrings that can be formed from string given by
a d e f b g h n m p
is
(1) 10
(2) 45
(3) 55
(4) 56
Solution) 56
Explanation)
Total number of non-empty substrings of all lengths from 1 to n
= n + (n-1) + (n-2) + (n-3) + … 2 + 1
= n * (n + 1)/2
These are non-empty substrings, but if you count null substrings there are [n(n+1)/2] + 1.
Where, n = 10,
So, total number of all substrings are = 10*11/2 + 1 = 55+1 = 56.
34. Consider the following two languages:
L1 = {x ∣ for some y with ∣y∣ = 2∣x∣,xy ∈ L and L is regular language}
L2 = {x ∣ for some y such that ∣x∣ = ∣y∣, xy ∈ L and L is regular language}
Which one of the following is correct?
Code:
(1) Only L1 is regular language
(2) Only L2 is regular language
(3) Both L1 and L2 are regular languages
(4) Both L1 and L2 are not regular languages
Solution) Both L1 and L2 are regular languages
Explanation) If we can express a language as regular expression then the language is regular.
35. Consider the following languages:
L1 = {an+m bn am ∣ n,m ≥ 0}
L2 = {an+m bn+m an+m ∣ n,m ≥ 0}
Which of the following is correct?
Code:
(1) Only L1 is context-free language
(2) Only L2 is context-free language
(3) Both L1 and L2 are context free languages
(4) Both L1 and L2 are not context free languages
Solution) Only L1 is context-free language
Explanation)
Since it is generated from the following CFG:
L1 = {anbmcn |m, n ≥ 1} is a context-free language.
S− > aSc|aBc;
B− > bB|b
• The pumping lemma can be used to argue that
• L2 = {anbnc2n |n ≥ 1} is not a context-free language. A pushdown automaton, on the surface, cannot recall the number of as for the third set of characters, i.e. c. This language is extremely similar to {anbncn |n ≥ 1} which is a non-CFL language.
As a result, the correct answer is (B). L1 is context-free, but L2 is not.
L2 is not a context-free language. The number of bs will match the number of as, leaving the cs to be matched with no one...so L2 can't be context-free.
36. Consider R to be any regular language and L1, L2 be any two context-free languages. Which of the following is correct?
(1) L1’ is context free
(2) (L1 ∪ L2)’ – R is context free
(3) L1 ∩ L2 is context free
(4) L1 – R is context free
Solution) L1 – R is context free
Explanation) Context-free languages are bound by union and distinction from regular languages.
Under complementation and intersection, it is not closed. Recursive language is a CFL complement.
37. Consider the following problems:
(i) Whether a finite state automaton halts on all inputs?
(ii) Whether a given context-free language is regular?
(iii) Whether a Turing machine computes the product of two numbers?
Which one of the following is correct?
Code:
(1) Only (i) and (iii) are undecidable problems
(2) Only (ii) and (iii) are undecidable problems
(3) Only (i) and (ii) are undecidable problems
(4) (i), (ii) and (iii) are undecidable problems
Solution) Only (i) and (iii) are undecidable problems
Explanation) Only (i) and (iii) are undecidable problems
Undecidable problems are those for which we can’t make an algorithm to give correct answers of the problem in finite time.
38. Which of the following problems is decidable for recursive languages (L)?
(1) Is L = ϕ?
(2) Is w ∈ L, where w is a string?
(3) Is L = Σ*?
(4) Is L = R, where R is a given regular set?
Solution) Is w ∈ L, where w is a string?
Explanation)
Only membership problem is decidable for Recursive languages
w∈L, where w is a string, is closed.
Answer is (2).
39. Consider the following grammar G:
S → A ∣ B
A → a ∣ c
B → b ∣ c
where {S, A, B} is the set of non-terminals, {a, b, c,} is the set of terminals.
Which of the following statement(s) is/are correct?
S1: LR(1) can parse all strings that are generated using grammar G.
S2: LL(1) can parse all strings that are generated using grammar G.
Choose the correct answer from the code given below:
Code:
(1) Only S1
(2) Only S2
(3) Both S1 and S2
(4) Neither S1 nor S2
Solution) Neither S1 nor S2
Explanation)
First(A) = {a,c}
First(B) = {b,c}
S → A | B ===> First(A) ∩ First(B) ≠ ∅ ===> it can't be LL(1)
Constructing LR(1) item-
Item 0-
S' → S, $
S → .A, $
S → .B, $
A → .a, $
A → .c, $
B → .b, $
B → .c, $
With c terminal variable on this item, we will go to, let Item K,
Item K -
A → c., $
B → c., $
Which is Reduce - Reduce Conflict ==> can't be parsed by LR(1)
40. The grammar S → (S) ∣ SS ∣ ϵ is not suitable for predictive parsing because the grammar is
(1) Right recursive
(2) Left recursive
(3) Ambiguous
(4) An operator grammar
Solution) Ambiguous
Explanation)
Since a given grammar can have an unlimited number of parse trees for the string ", it is ambiguous, and A →AA has left recursion.
Grammar for predictive parsing should be:
Without any uncertainty
Recursion to the left is no longer an issue.
Unaffected by left factoring
Given that the grammar incorporates both ambiguity and left factoring, a predictive parser is not possible.
For parsing, we always anticipate the first grammar to be devoid of ambiguity.
41. If the frame buffer has 10-bits per pixel and 8-bits are allocated for each of the R,G, and B components, then what would be the size of the color lookup table (LUT)?
(1) (28+29) bytes
(2) (210+28) bytes
(3) (210+224) bytes
(4) (210+211) bytes
Solution) (210+211) bytes
Explanation)
Each pixel in the frame buffer has ten bits, while each R, G, and B component has eight bits.
The frame buffer is a ten-bit buffer. As a result, the number of entries in the colour lookup table is 210.
Each component has an 8-bit value. All three components have a total of 24 bits.
It means that the R, G, and B components each take up 24/8 = 3 bytes.
Look up the colour size. table = number of lookup table entries x size of each entry
The size of the lookup table is 210 x 3 = 3072 bytes (210 + 211).
42.Which homogeneous 2D matrix transforms the figure (a) on the left side to the figure (b) on the right?
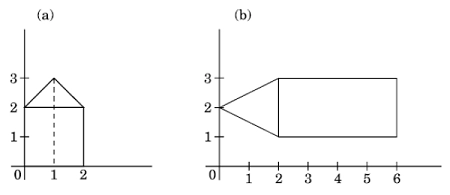
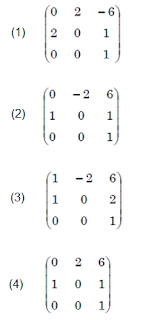
Solution) (2)
Explanation)
Right figure is rotated 90 degrees anti clockwise. We know that matrix after rotation in case of anticlockwise rotation look like-
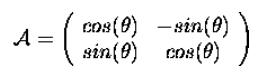
We have to transform a given 2D matrix into a 3D homogeneous matrix system because all the options are given in 3D matrix. Hence same will look like -
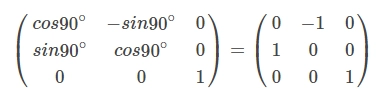
Here rotation is done w.r.t 2 and options are there which are matching for the same. So, there is no need to do it again.
Matrix after rotation with respect to 2 looks like -
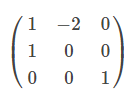
Position of - (negative) sign can clearly tell that answer can option B or C. So to find the correct one we will go further. As we know that we get translation matrix by -
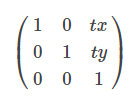
Here now the point which is at (0,0) is transformed to 6 and 1 along the x-axis and y-axis.
tx=6 and ty=1 putting values we get a matrix we looks like -
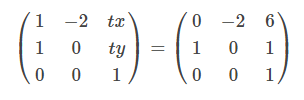
43.Consider the midpoint (or Bresenham) algorithm for rasterizing lines given below:
Input (x1, y1) and (x2, y2)
y = y1
d = f(x1 + 1, y1 + 1/2) //f is the implicit form of a line
for x = x1 to x2
do
plot(x,y)
if (d<0)
then
y = y+1
d = d+(y1−y2) + (x2−x1)
else
d = d+(y1−y2)
end
end
Which statements are true?
P: For a line with slope m>1, we should change the outer loop in line (4) to be over y
Q: Lines (10) and (12) update the decision variable d through an incremental evaluation of the line equation f
R: The algorithm fails if d is over 0
Choose the correct answer from the code given below:
Code:
(1) P only
(2) P and Q only
(3) Q and R only
(4) P, Q and R
Solution) P and Q only
Explanation)
Statement P: We should update the outer loop in line (4) to be over y for a line with slope m>1.
Line 4) should be adjusted to be over y and slope m > 1 for x = x1 to x2.
m = (y2 – y1)/ (x2 – x1) is the slope of a line. Because it now relies on x coordinates, it should now rely on y coordinates to be over y.
Statement Q: Lines ten and twelve incrementally evaluate the line equation f to update the decision variable d.
Lines (10) and (12) of the method clearly explain how incremental evaluation is used to change the values of d. Adding d to itself, in other words.
d = d + (y1 - y2) + (x2 - x1) ---- line (10)
d = d + (y1 - y2) ---- line (12)
R: If d is ever 0 the algorithm fails
When d is 0, the algorithm does not fail. because when d >=0 then it moves to line 12 and computes the value of. So, this statement is false.
44.In 3D Graphics, which of the following statements about perspective and parallel projection is/are true?
P: In a perspective projection, the farthest an object is from the centre of projection, the smaller it appears.
Q: Parallel projection is equivalent to a perspective projection where the viewer is standing infinitely far away.
R: Perspective projections do not preserve straight lines.
Choose the correct answer from the code given below:
Code:
(1) P and Q only
(2) P and R only
(3) Q and R only
(4) P, Q and R
Solution) P and Q only
Explanation) One of the most essential characteristics of perspective projections is that they retain straight lines, allowing us to project only the endpoints of 3D lines and then create a 2D line between them.
All of the statements are true.
45.In 3D Graphics, which of the following statements is/are true?
P: Back-face culling is an example of an image-precision visible-surface determination procedure.
Q: Z- buffer is a 16-bit, 32-bit, or 64 bit field associated with each pixel in a frame buffer that can be used to determine the visible surfaces at each pixel.
Choose the correct answer from code given below:
Code:
(1) P only
(2) Q only
(3) P and Q
(4) Neither P nor Q
Solution) Q only
Explanation)
This assertion is correct. A visible surface detecting approach is the Z buffer. This method is sometimes referred to as the depth buffer method. During the surface processing, depth values are kept for each position (x, y). In this method, each surface is processed separately. Pixel depth values are compared, and the colour or surface to be displayed is determined by the least z value. The visible surface at each pixel can be determined using the Z-buffer, which is a 16-bit, 32-bit, or 64-bit field associated with each pixel in a frame buffer.
46.Consider the following pseudo-code fragment, where m is a non-negative integer that has been initialized:
p = 0
k = 0
while (k<m)
p = p + 2k
k = k + 1
end while
Which of the following is a loop invariant for the while statement?
(Note: a loop invariant for a while statement is an assertion that is true each time the guard is evaluated during the execution of the while statement).
(1) p = 2k − 1 and 0≤k<m
(2) p = 2k+1 − 1 and 0≤k<m
(3) p = 2k − 1 and 0≤k≤m
(4) p = 2k+1 − 1 and 0≤k≤m
Solution) p = 2k − 1 and 0≤k≤m
Explanation)
k=0, p=0
After first iteration, p=0+20= 1, k=1
After nth iteration, p=20+21 + . . . . + 2n-1= 2n - 1, k=n
When the loop will run for m iterations then 0 k m
47. Consider the following two C++ programs P1 and P2 and two statements S1 and S2 about these programs:

S1: P1 prints out 3.
S2: P2 prints out 4:2
What can you say about the statements S1 and S2?
Code:
(1) Only S1 is true
(2) Only S2 is true
(3) Both S1 and S2 are true
(4) Neither S1 nor S2 is true
Solution) Only S1 is true
Explanation)
f(i,&i,i); --> f(int a,int *b,int &c);
‘a’ gets a variable's copy which was passed.
‘B’ points to a passed variable to it which is i.
‘&c’ passing i by reference.
a = 1; //original i remains unaffected, copy of i value get updated
*b = 2; //original i=2 gets updated;
c = 3; //original i=3 gets updated;
cout<<i;
Here, i =3 will be printed, so S1 is true.
f(a) = 5;
f(a) calls the function f,
double &f(double &d){
d=4;
return b;
}
This function is taking a reference variable as a parameter and updating its value to 4 that is a = 4 and returning a reference to double b.
f(a)=5; ////original b=5 gets updated;
cout<<a<<":"<<b; //prints 4 : 5
S2 should be false for the above code.
48. Consider the following recursive Java function f that takes two long arguments and returns a float value:
public static float f(long m, long n)
{
float result = (float) m / (float) n;
if (m < 0 || n < 0)
return 0.0f;
else
result += f(m*2, n*3);
return result;
}
Which of the following integers best approximates the value of f(2,3)?
(1) 0
(2) 1
(3) 2
(4) 3
Solution) 2
Explanation)
The values are passed to m,n using the function f(1,3). The value will then be typecast to float with the result=0.3333. The function f is f then enters the else statement (2,9).
Finally, 0.20000003 is returned as the result. As a result, 0.2 is the correct answer.
49. What does the following Java function perform? (Assume int occupies four bytes of storage)
public static int f(int a)
{ // Pre-conditions : a > 0 and no overflow/underflow occurs
int b=0;
for (int i=0; i<32; i++)
{
b = b<<1;
b = b | (a & 1);
a = a >>>1; // This is a logical shift
}
return b;
}
(1) Returns the int that has the binary representation of integer a
(2) Return the int that has the reversed binary representation of integer a
(3) Return the int that represents the number of 1’s in the binary representation of integer a
(4) Return the int that represents the number of 0’s in the binary representation of integer a
Solution) Return the int that has the reversed binary representation of integer a
Explanation)
Initially value of b = 0, Considering a = 5
Iteration 1:
for(int i=0; i<32; i++) //condition is true
b = b<<1; // b becomes 0 (0 × 2 = 0)
b= b | (a & 1); // 0 | (5 & 1) ; b becomes 1
a = a >>> 1; // as this is a logical shift; so a becomes 2
Iteration 2 :
for(int i=0; i<32; i++) // i is 1, condition is true
b = b<<1; // b becomes 2
b= b | (a & 1); // 2|(2 & 1) ; b becomes 2
a = a >>> 1; // as this is a logical shift; so a becomes 1
Iteration 3:
for(int i=0; i<32; i++) // i is 2, condition is true
b = b<<1; // b becomes 4
b= b | (a & 1); // 4|(1 & 1) ; b becomes 5
a = a >>> 1; // as this is a logical shift; so a becomes 0
Iteration 4:
for(int i=0; i<32; i++) // i is 3, condition is true
b = b<<1; // b becomes 10
b= b | (a & 1); // 10|(0 & 1) ; b becomes 1o
a = a >>> 1; // as this is a logical shift; so a becomes 0
Value of b will multiply by 2 on every iteration after this.
when i = 4, b = 20
when i = 5, b = 40
when i = 6, b = 80 = 23 × 10
when i = 7, b = 160 = 24 × 10
….
when i = 29, b = 160 = 226 × 10
when i = 30, b = 227 × 10
But in java size of int is 4 byte: Range - 231 to 231 – 1
when i = 30, b = 227 × 10 ≡ -1610612736
when i = 31, b = 228 × 10 ≡ -1610612736
a = 5 = (0000 0000 …. 0101)2
reverse of a = 1010 0000 0000 …. 0000)2 = -231 + 229 = -1610612736
Therefore, it returns the int that has the reversed binary representation of integer a.
50. In a ternary tree, the number of internal nodes of degree 1, 2, and 3 is 4, 3, and 3 respectively. The number of leaf nodes in the ternary tree is
(1) 9
(2) 10
(3) 11
(4) 12
Solution) 10
Explanation)
By looking at the degrees of nodes, we get to know that TREE is assumed as Directed graph.
Let Ni represents Number of Nodes with Degree i
Total No. of Nodes in a Tree = N0 + N1 + N2 + N3
A tree has exactly n-1 edges with N nodes.
∴ N = |E| + 1 ==> N0 + N1+ N2 + N3 = |E| + 1 --------- (1)
Given that, N1 = 4 , N2 = 3 , N3 = 3
Total Edges in the directed graph = summation of all degrees = ∑ Ni . i
∴ | E | = ( 0*N0) + (1*N0) + (2*N2) + (3*N3) = ( 0*?) + (1*4) + (2*3) + (3*3) = 0+4+6+9 = 19
Substitute this value in eqn (1),
N0 + N1 + N2 + N3 = 19 + 1N0 + 4+3+3 = 19+1 ===> N0 + 10 = 20 ===> N0 = 10




