What is the time complexity of delete operation in a b-tree?

The average time complexity of delete operation is O(logn) and worst-case time complexity is also O(logn), where n is the number of the elements in the b-tree.

What is the space complexity of delete operation in a b-tree?

The space complexity of delete operation is O(n), where n is the number of elements in the b-tree.

Are b-tree fully balanced or partially balanced?

The b-tree is a fully balanced tree.

Table of contents

Introduction

Deletion in B-tree

2.1.

Deletion From Leaf Node.

2.1.1.

If Node Has More Than MIN Keys,

2.1.2.

If Node Has MIN Keys

2.2.

Deletion From Non-Leaf Node,

Implementation in C++

FAQs

Key takeaways

Last Updated: Mar 27, 2024

Delete Operation in B-Tree

Author Ankit Kumar

Do you think IIT Guwahati certified course can help you in your career?

Yes

Introduction

Before we directly jump into today's discussion, it is imperative to collect all the properties of B-Tree to understand the Delete operation. So, let's revisit them:

B Tree is a self-balancing Data Structure that uses a set of rules to search, insert, and delete data in a faster and more memory-efficient manner. The following rules are followed to create a B Tree to accomplish this.

Rule 1: All leaf nodes must be at the same level.

Rule 2: All non-leaf nodes (except the root node) should have children at least [m/2].

Rule 3: All nodes ( except the root node) should have at least [m/2] - 1 key.

Rule 4: If the root node is a leaf node(only node in the tree), it will have no children and at least one key. If the root node is a non-leaf node, it will have at least two children and one key.

Rule 5: A non-leaf node with n-1 key values should have n non-null children.

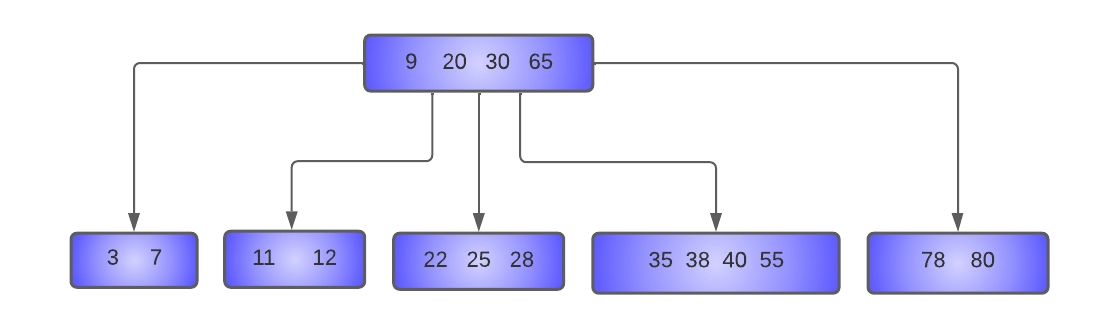
From the below pictorial representation, we can obtain the properties of a B-Tree:

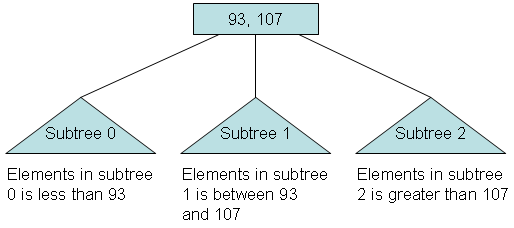
From the definition, we can conclude that any node except the root node in a B-Tree is half full, which avoids wastage of storage space. The B-Tree is perfectly balanced, so the number of nodes accessed to find a key decreases.

The following figure shows the minimum and a maximum number of children in any non-root and non-leaf node of B-trees of different orders.

Order of the tree	Minimum Children (MIN)	Maximum Children(MAX)
4	2	4
5	3	5
M	[M/2]	M

Also See, Multiple Granularity in DBMS and Checkpoint in DBMS.

Deletion in B-tree

While inserting a key, we had to ensure that the number of keys should not exceed MAX. Similarly, while deleting, we must watch that the number of keys in a node should not become less than MIN. While inserting, when the keys exceed MAX, we split the node into two nodes, and the median key went to the parent node; while deleting when the keys will become less than MIN, we will combine two nodes into one.

Now let us see how all this is done by studying the deletion cases. Deletion in a B-Tree can be classified into two cases:

Deletion from the leaf node.
Deletion from the non-leaf node.

Let us now elaborate on each case:

Deletion From Leaf Node.

It will be divided into various cases. Let us study every case in detail.

If Node Has More Than MIN Keys,

In this case, deletion is very straightforward, and the key can be very easily deleted from the node by shifting other keys of the node.

If Node Has MIN Keys

After the deletion of a key, the node will have less than MIN keys and will become an underflow node. In such a case, we can borrow a key from the left or right sibling if any one of them has more than MIN keys.

Now you must be wondering which sibling to start from?

In our algorithm, we'll first try to borrow a key from the left sibling; if the left sibling has only MIN keys, then we'll try to borrow from the right sibling.

When a key is borrowed from the left sibling, the separator key in the parent is moved to the underflow node, and the last key from the left sibling is moved to the parent.
When a key is borrowed from the right sibling, the separator key in the parent is moved to the underflow node, and the first key from the right sibling is moved to the parent. All the remaining keys in the right sibling are moved from one position to the left.

Time for some examples:

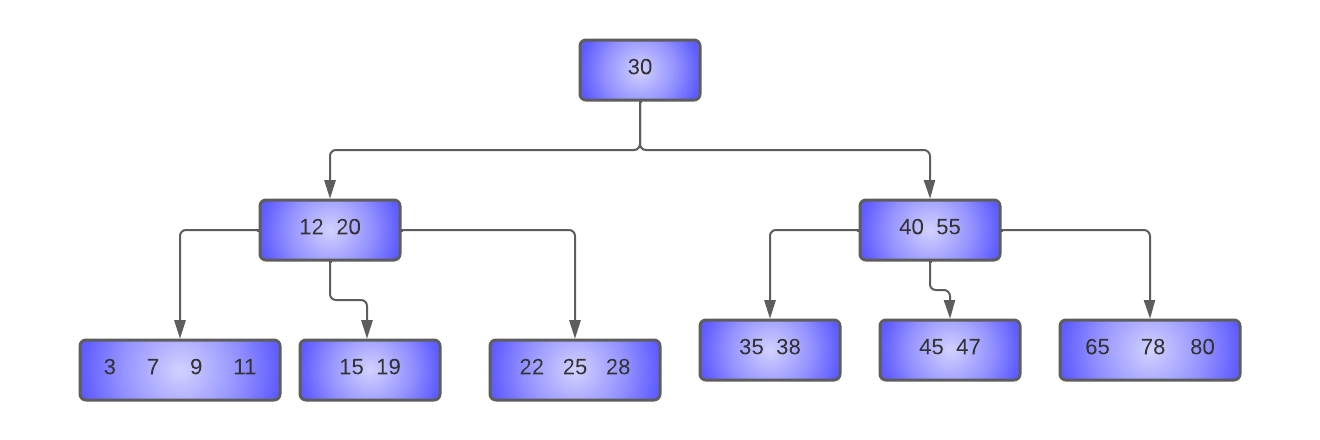
Delete 15 from the tree:

Here key 15 is to be deleted from the node [15, 19]. Since this node has only MIN keys, we will try to borrow from its left sibling[ 3,7,9,11], which has more than MIN keys.

The parent of these nodes is node [12, 20], and the separator key is 12. Hence, the last key of the left sibling (11) is moved to the place of the separator key, which is moved to the underflow node.

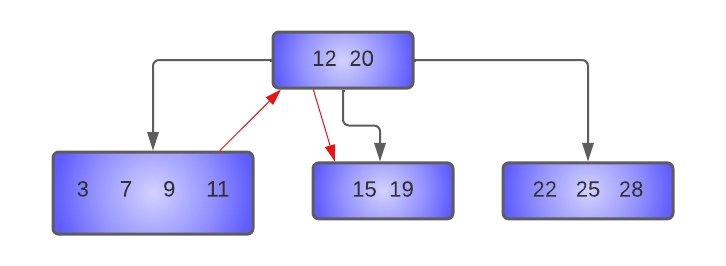
The resulting tree after deletion of 15 will be:-

Note: The involvement of the separator key is necessary since if we simply borrow 11 and put it at the place of 15, then the property of the B-tree will be violated.

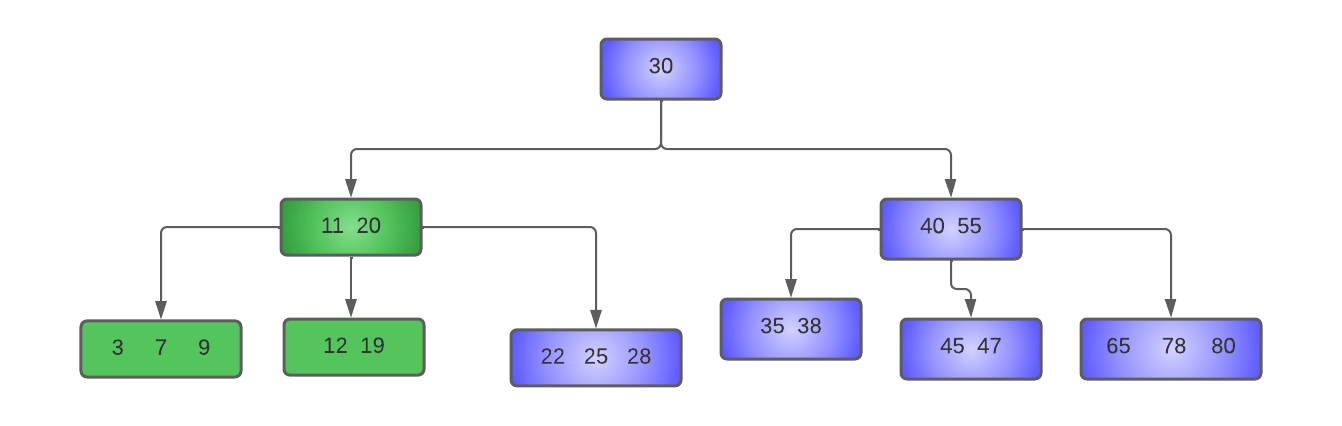
Delete 19 from the tree:

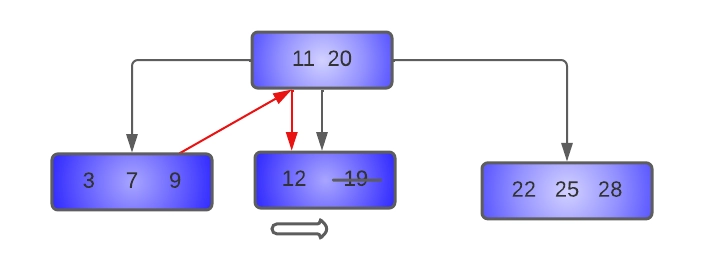
As we can see above, key 19 will be deleted by borrowing the left sibling, so key nine will be moved up to the parent node, and 11 will be shifted to the underflow node. In the underflow node, the key 12 will be shifted to the right to make place for 11. The resultant tree will look like this:

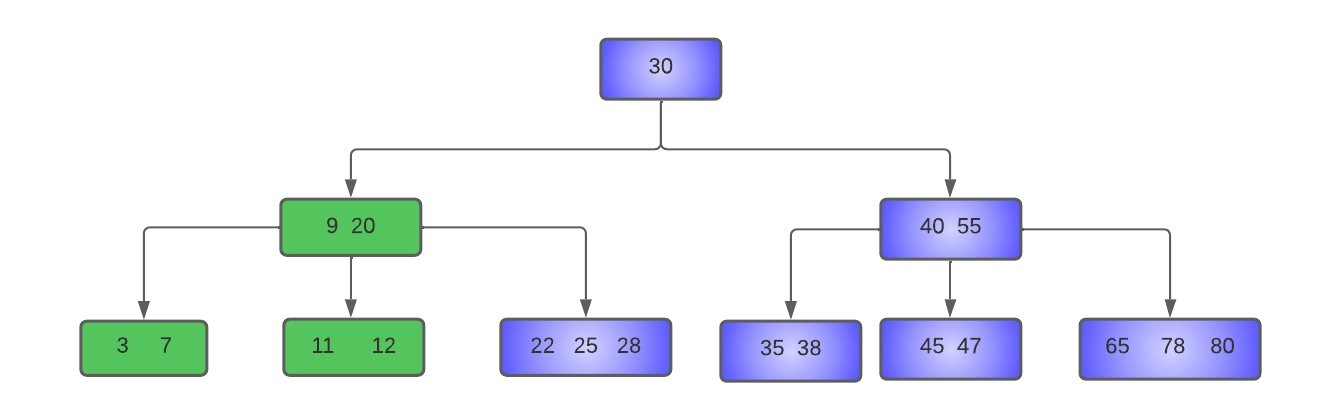
Delete 45 from the tree:

As we can see in the diagram itself, the left sibling of the [45, 47] is [35, 38], which has only MIN keys, so we can't borrow from it. Thus, we will try to borrow from the right sibling, i.e., [65, 78, 80]. As discussed above, while borrowing from the right sibling, the first key of the node is moved to the parent node. In this case, the first key of the right sibling(65) will be moved to the parent node, and the separator key from the parent node(55) will be moved to the underflow node.

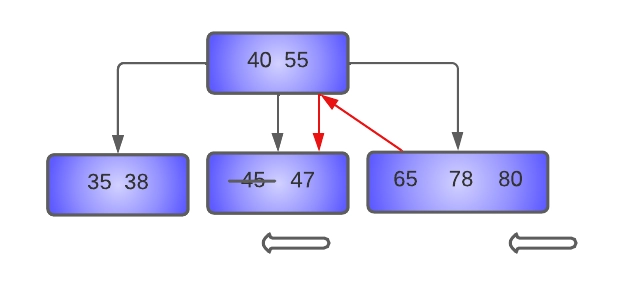
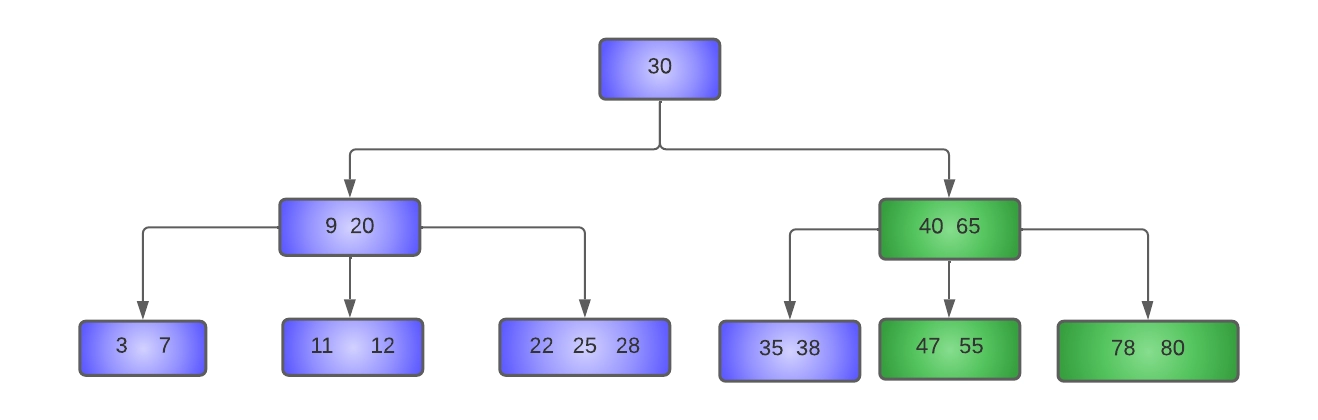
In the underflow node, 47 is shifted left to make room for 55. In the right sibling, 78 and 80 are moved to the left to fill the gap created by the removal of 65.

The resulting tree will look like this:

Note: If both left and right siblings of the underflow node have MIN keys, then we can’t borrow from any of the siblings. In this case, the underflow node is combined with its left( or right ) sibling.

Let’s see an example for the same:

Delete 47 from the tree:

If we try to delete 47 from the tree which has only MIN keys and if we delete it, it leads to the underflow condition, so we'll try to borrow from the left sibling [ 35, 38], which also has only MIN keys, then we try to borrow from the right sibling [ 78, 80] which has again MIN keys only. So, what should we do now?

We’ll combine the left sibling node with the key left in the current node. For combining these two nodes, the separator key(40) from the parent node will move down in the combined node.

But the parent node also has only MIN keys.

In this case, when the parent node becomes underflow, we will borrow a key from its left sibling. But if we look at its left sibling, it also has only MIN keys.

Here, the separator key ( 30) the root node comes down in the combined node, which becomes the new root of the tree, and the height of the tree decreases by one.

The resulting tree will look like this:

Deletion From Non-Leaf Node,

In this case, the successor key is copied at the place of the key to be removed, and then the successor is deleted. The successor key is the smallest key in the right subtree and will always be in the leaf node. So this case reduces to the above-mentioned approaches.

Let’s retake the above B-tree example:

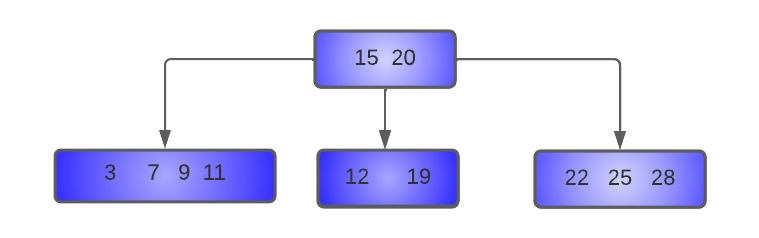
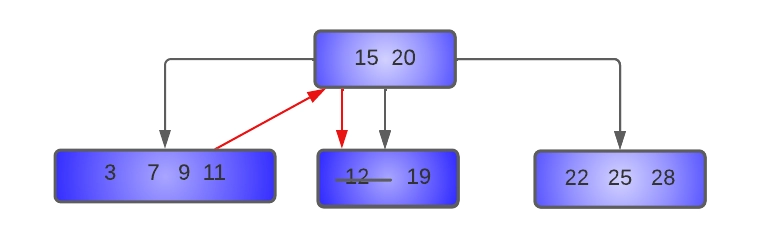
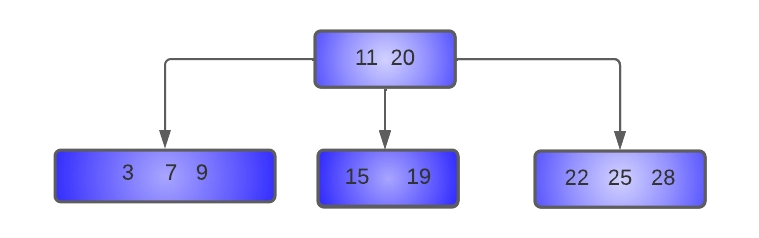
Delete 12 from the tree:

The successor key of 12 is 15, this we’ll copy 15 at the place of 12, and now our task reduces to deletion of 15 from the leaf node. This deletion is performed by borrowing a key from the left sibling.

Now let us conclude the above discussion by looking at the flowchart:

Now that you have gained a good understanding of how deletion takes place in B-Tree, it's time to look at its Implementation:

You can also read about the Multiple Granularity Locking and Recursive Relationship in DBMS.

Implementation in C++

// Implementation of deletion operation in B-tree 
#include <bits/stdc++.h>
using namespace std;
class BTreeNode {
  int *keys;
  int t;
  BTreeNode **C;
  int n;
  bool leaf;
   public:
  BTreeNode(int _t, bool _leaf);
  void traverse();
  int searchkey(int k);
  void insert_Non_Full(int k);
  void split_Child(int i, BTreeNode *y);
  void deletion(int k);
  void remove_From_Leaf(int idx);
  void remove_From_Non_Leaf(int idx);
  int get_Predecessor(int idx);
  int get_Successor(int idx);
  void fill(int idx);
  void borrow_From_Prev(int idx);
  void borrow_From_Next(int idx);
  void merge(int idx);
  friend class BTree;
};
class BTree {
  BTreeNode *root;
  int t; 
   public:
  BTree(int _t) {
    root = NULL;
    t = _t;
  } 
  void traverse() {
    if (root != NULL)
      root->traverse();
  } 
  void insertion(int k);
  void deletion(int k);
};
// B tree node
BTreeNode::BTreeNode(int t1, bool leaf1) {
  t = t1;
  leaf = leaf1; 
  keys = new int[2 * t - 1];
  C = new BTreeNode *[2 * t];
  n = 0;
} 
// Find the key
int BTreeNode::searchkey(int k) {
  int idx = 0;
  while (idx < n && keys[idx] < k)
    ++idx;
  return idx;
}
// Deletion operation
void BTreeNode::deletion(int k) {
  int idx = searchkey(k);
  if (idx < n && keys[idx] == k) {
    if (leaf)
      remove_From_Leaf(idx);
    else
      remove_From_Non_Leaf(idx);
  } else {
    if (leaf) {
      cout << "key " << k << " does not exist in the tree\n";
      return;
    }
    bool flag = ((idx == n) ? true : false);
    if (C[idx]->n < t)
      fill(idx);
    if (flag && idx > n)
      C[idx - 1]->deletion(k);
    else
      C[idx]->deletion(k);
  }
  return;
} 
// Remove from the leaf
void BTreeNode::remove_From_Leaf(int idx) {
  for (int i = idx + 1; i < n; ++i)
    keys[i - 1] = keys[i];
  n--;
  return;
} 
// Delete from non leaf node
void BTreeNode::remove_From_Non_Leaf(int idx) {
  int k = keys[idx]; 
  if (C[idx]->n >= t) {
    int pred = get_Predecessor(idx);
    keys[idx] = pred;
    C[idx]->deletion(pred);
  } 
  else if (C[idx + 1]->n >= t) {
    int succ = get_Successor(idx);
    keys[idx] = succ;
    C[idx + 1]->deletion(succ);
  } 
  else {
    merge(idx);
    C[idx]->deletion(k);
  }
  return;
} 
int BTreeNode::get_Predecessor(int idx) {
  BTreeNode *cur = C[idx];
  while (!cur->leaf)
    cur = cur->C[cur->n];
  return cur->keys[cur->n - 1];
}
int BTreeNode::get_Successor(int idx) {
  BTreeNode *cur = C[idx + 1];
  while (!cur->leaf)
    cur = cur->C[0];
  return cur->keys[0];
}
void BTreeNode::fill(int idx) {
  if (idx != 0 && C[idx - 1]->n >= t)
    borrow_From_Prev(idx);
  else if (idx != n && C[idx + 1]->n >= t)
    borrow_From_Next(idx);
  else {
    if (idx != n)
      merge(idx);
    else
      merge(idx - 1);
  }
  return;
}
// Borrow from previous
void BTreeNode::borrow_From_Prev(int idx) {
  BTreeNode *child = C[idx];
  BTreeNode *sibling = C[idx - 1];
  for (int i = child->n - 1; i >= 0; --i)
    child->keys[i + 1] = child->keys[i];
  if (!child->leaf) {
    for (int i = child->n; i >= 0; --i)
      child->C[i + 1] = child->C[i];
  }
  child->keys[0] = keys[idx - 1];
  if (!child->leaf)
    child->C[0] = sibling->C[sibling->n]; 
  keys[idx - 1] = sibling->keys[sibling->n - 1];
  child->n += 1;
  sibling->n -= 1;
  return;
}
// Borrow from the next
void BTreeNode::borrow_From_Next(int idx) {
  BTreeNode *child = C[idx];
  BTreeNode *sibling = C[idx + 1];
  child->keys[(child->n)] = keys[idx];
  if (!(child->leaf))
    child->C[(child->n) + 1] = sibling->C[0];
  keys[idx] = sibling->keys[0];
  for (int i = 1; i < sibling->n; ++i)
    sibling->keys[i - 1] = sibling->keys[i];
  if (!sibling->leaf) {
    for (int i = 1; i <= sibling->n; ++i)
      sibling->C[i - 1] = sibling->C[i];
  }
  child->n += 1;
  sibling->n -= 1;
  return;
}
// Merge
void BTreeNode::merge(int idx) {
  BTreeNode *child = C[idx];
  BTreeNode *sibling = C[idx + 1];
  child->keys[t - 1] = keys[idx];
  for (int i = 0; i < sibling->n; ++i)
    child->keys[i + t] = sibling->keys[i];
  if (!child->leaf) {
    for (int i = 0; i <= sibling->n; ++i)
      child->C[i + t] = sibling->C[i];
  } 
  for (int i = idx + 1; i < n; ++i)
    keys[i - 1] = keys[i];
  for (int i = idx + 2; i <= n; ++i)
    C[i - 1] = C[i]; 
  child->n += sibling->n + 1;
  n--;
  delete (sibling);
  return;
} 
// Insertion operation
void BTree::insertion(int k) {
  if (root == NULL) {
    root = new BTreeNode(t, true);
    root->keys[0] = k;
    root->n = 1;
  } else {
    if (root->n == 2 * t - 1) {
      BTreeNode *s = new BTreeNode(t, false);
      s->C[0] = root;
      s->split_Child(0, root);
      int i = 0;
      if (s->keys[0] < k)
        i++;
      s->C[i]->insert_Non_Full(k);
      root = s;
    } else
      root->insert_Non_Full(k);
  }
}
// Insertion non full
void BTreeNode::insert_Non_Full(int k) {
  int i = n - 1;
  if (leaf == true) {
    while (i >= 0 && keys[i] > k) {
      keys[i + 1] = keys[i];
      i--;
    }
    keys[i + 1] = k;
    n = n + 1;
  } else {
    while (i >= 0 && keys[i] > k)
      i--;
    if (C[i + 1]->n == 2 * t - 1) {
      split_Child(i + 1, C[i + 1]);

 
      if (keys[i + 1] < k)
        i++;
    }
    C[i + 1]->insert_Non_Full(k);
  }
} 
// Split child
void BTreeNode::split_Child(int i, BTreeNode *y) {
  BTreeNode *z = new BTreeNode(y->t, y->leaf);
  z->n = t - 1;
  for (int j = 0; j < t - 1; j++)
    z->keys[j] = y->keys[j + t];
  if (y->leaf == false) {
    for (int j = 0; j < t; j++)
      z->C[j] = y->C[j + t];
  }
  y->n = t - 1;
  for (int j = n; j >= i + 1; j--)
    C[j + 1] = C[j];
  C[i + 1] = z;
  for (int j = n - 1; j >= i; j--)
    keys[j + 1] = keys[j];
  keys[i] = y->keys[t - 1];
  n = n + 1;
}
// Traverse
void BTreeNode::traverse() {
  int i;
  for (i = 0; i < n; i++) {
    if (leaf == false)
      C[i]->traverse();
    cout << " " << keys[i];
  }
  if (leaf == false)
    C[i]->traverse();
}
// Delete Operation
void BTree::deletion(int k) {
  if (!root) {
    cout << "The tree is empty\n";
    return;
  }
  root->deletion(k);
  if (root->n == 0) {
    BTreeNode *tmp = root;
    if (root->leaf)
      root = NULL;
    else
      root = root->C[0]; 
    delete tmp;
  }
  return;
} 
int main() {
  BTree bt(3);
  int key;
  bt.insertion(8);
  bt.insertion(9);
  bt.insertion(10);
  bt.insertion(11);
  bt.insertion(15);
  bt.insertion(16);
  bt.insertion(17);
  bt.insertion(18);
  bt.insertion(20);
  bt.insertion(23);
  cout << "The B-tree is: "<<endl;
  bt.traverse();
  cout<<"\nEnter key you want to delete from the B-tree:"<<endl;
  cin>>key; 
  bt.deletion(key);
  cout << "\nThe B-tree after deletion " << key <<" is: ";
  bt.traverse();
  cout<<"\nHAPPY LEARNING"; 
}

You can also try this code with Online C++ Compiler

Run Code

Output

The B-tree is:

8 9 10 11 15 16 17 18 20 23

Enter key you want to delete from the B-tree:

The B-tree after deletion 20 is: 8 9 10 11 15 16 17 18 23

HAPPY LEARNING

Let us now answer some of the frequently asked questions related to it.

Recommended Topic - Specialization and Generalization in DBMS

FAQs

What is the time complexity of delete operation in a b-tree?
The average time complexity of delete operation is O(logn) and worst-case time complexity is also O(logn), where n is the number of the elements in the b-tree.
What is the space complexity of delete operation in a b-tree?
The space complexity of delete operation is O(n), where n is the number of elements in the b-tree.
Are b-tree fully balanced or partially balanced?
The b-tree is a fully balanced tree.

Let us now summarize the long, long article.

Key takeaways

In this article, we learned about a balanced tree known as the b-tree, which is used in storing data. The prime focus was to explain the delete operation in it. We covered all the possible causes of deletion and explained you with the help of several diagrams, examples, and flowcharts. It was followed by Implementation of it in C++, and in the last, we answered some of the frequently asked questions.
Check out this problem - Largest BST In Binary Tree

Ninjas! Do not stop here and explore Coding Ninjas Studio and also practice some of the Top 100 SQL problems.