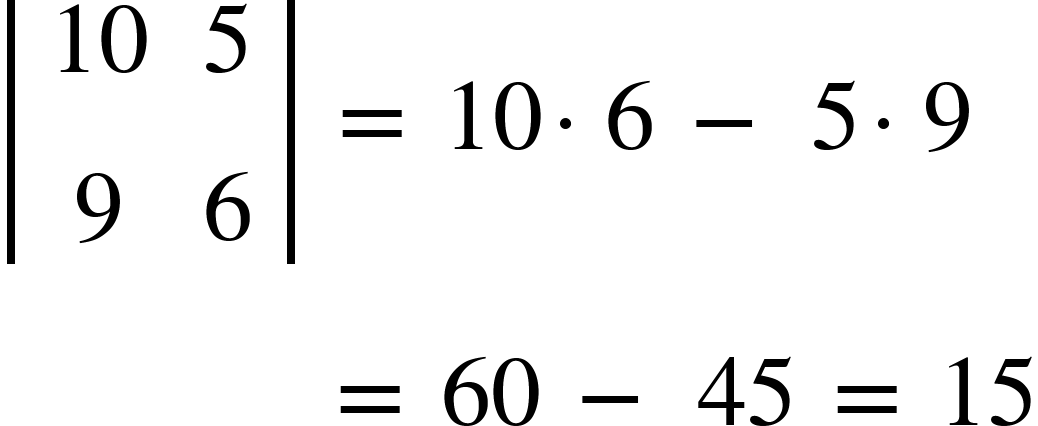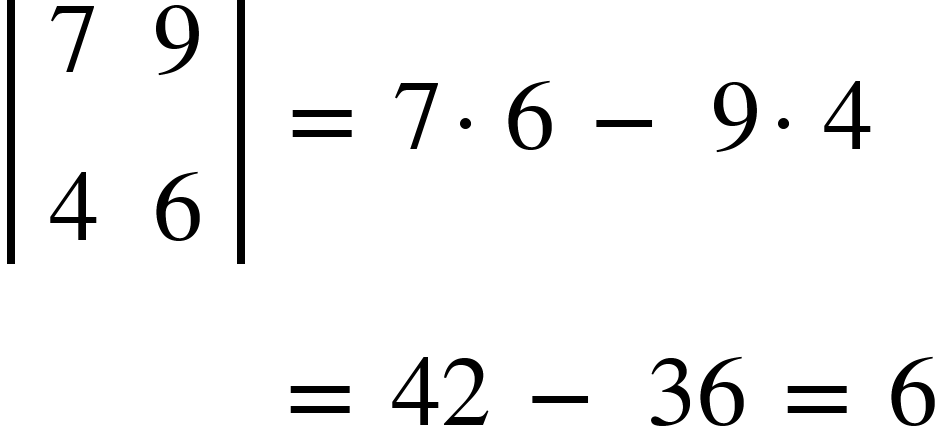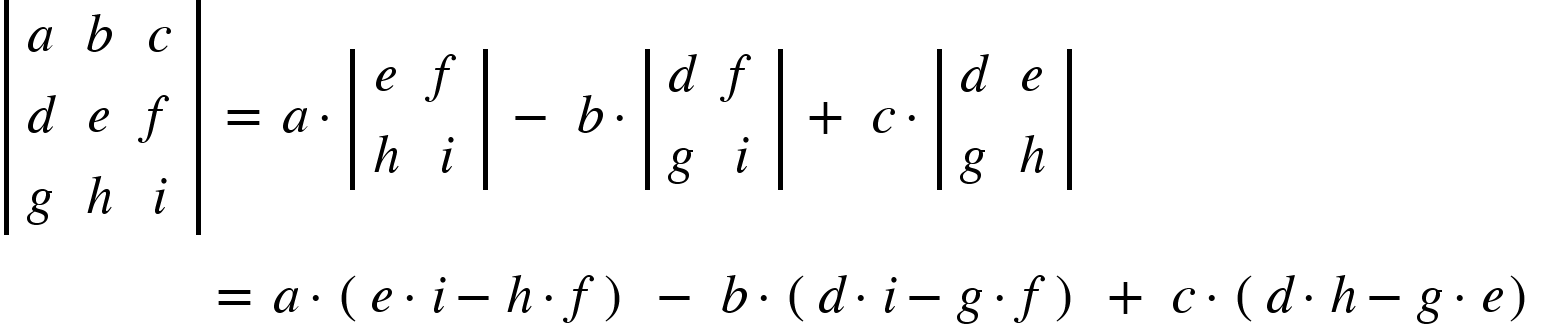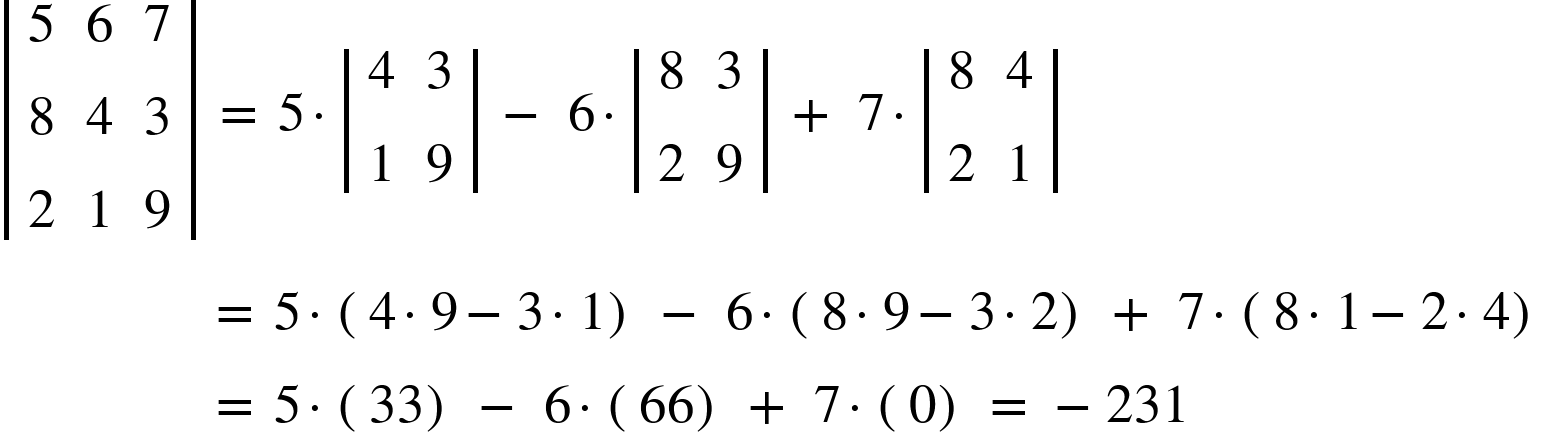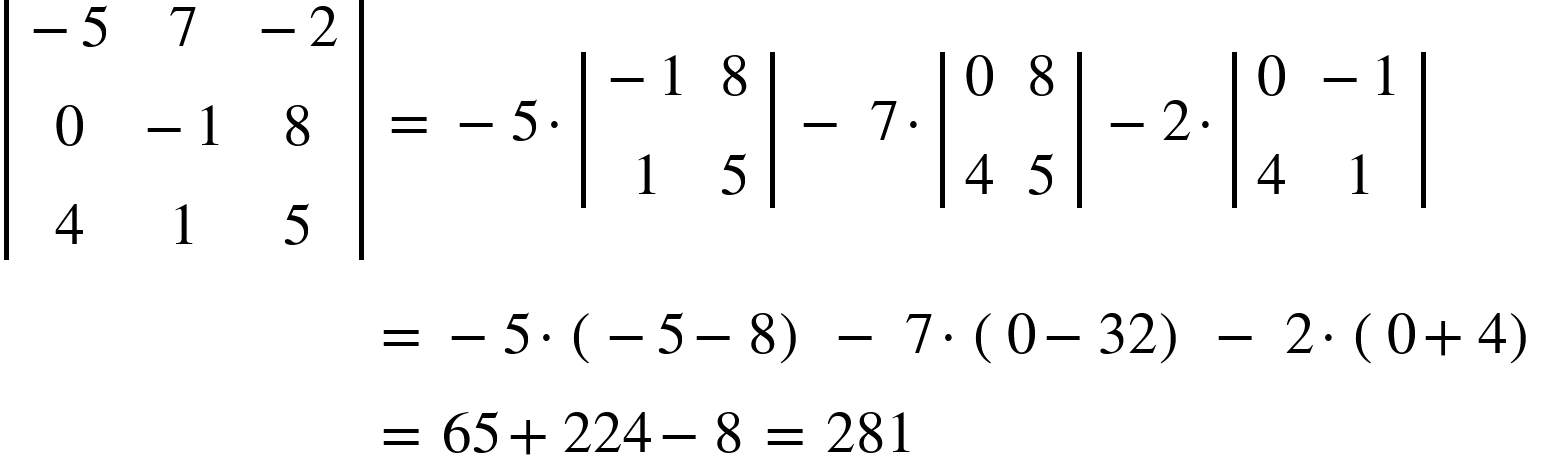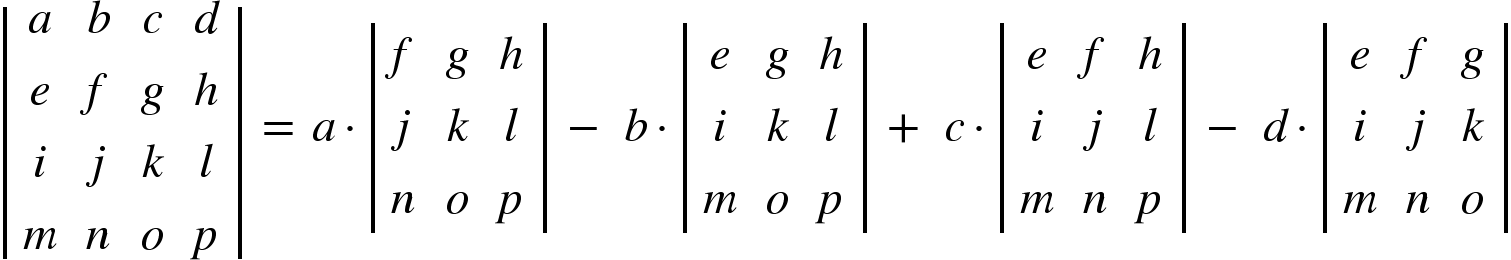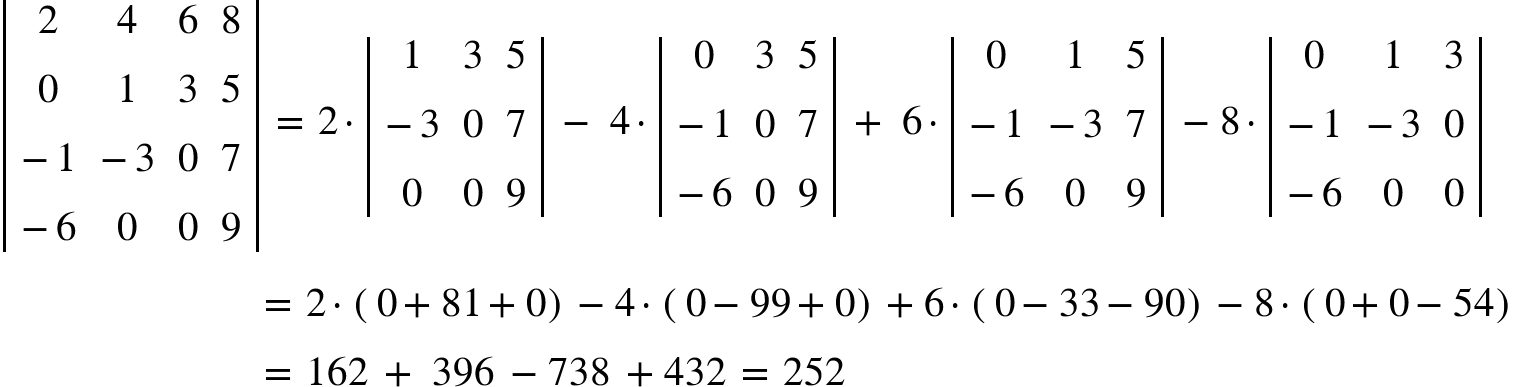Evaluation of Determinants
We will learn the evaluation of 2nd, 3rd, and 4th order determinants one by one.
Evaluation of 2nd Order Determinant
Determinant of order 2 is determined by:
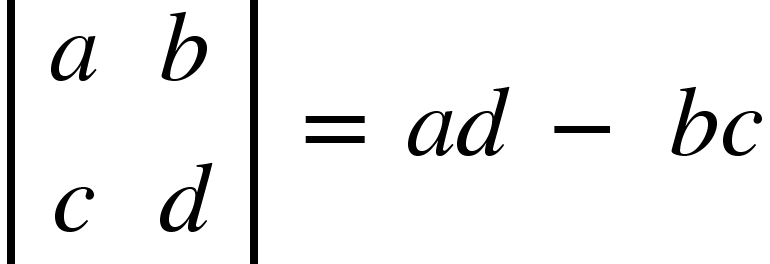
Examples:
a.)
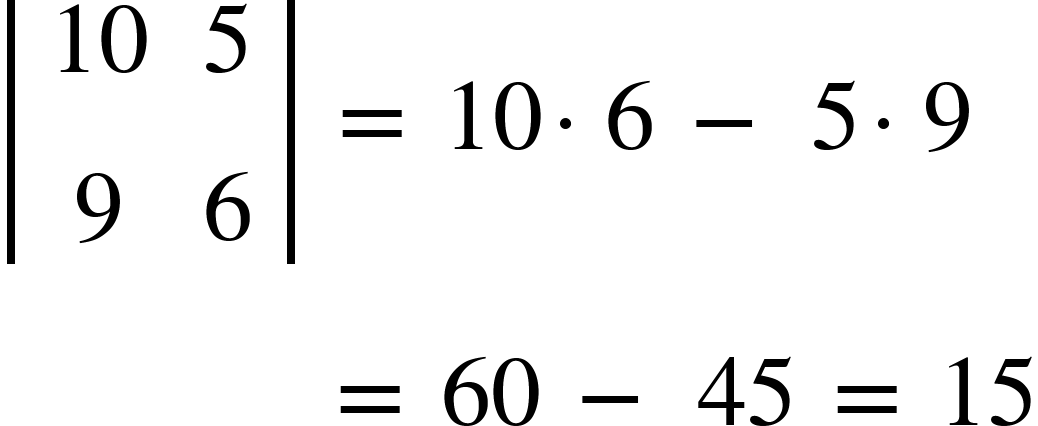
b.)
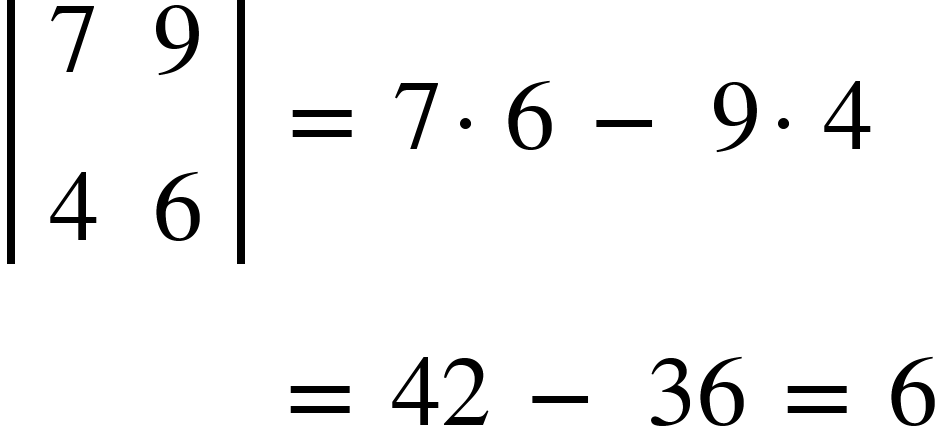
Evaluation of 3rd Order Determinant
A third-order or  the determinant can be written as:
the determinant can be written as:
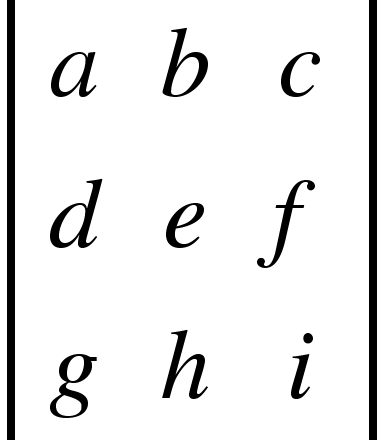
It can be evaluated with the help of the 2nd order determinant, as shown below.
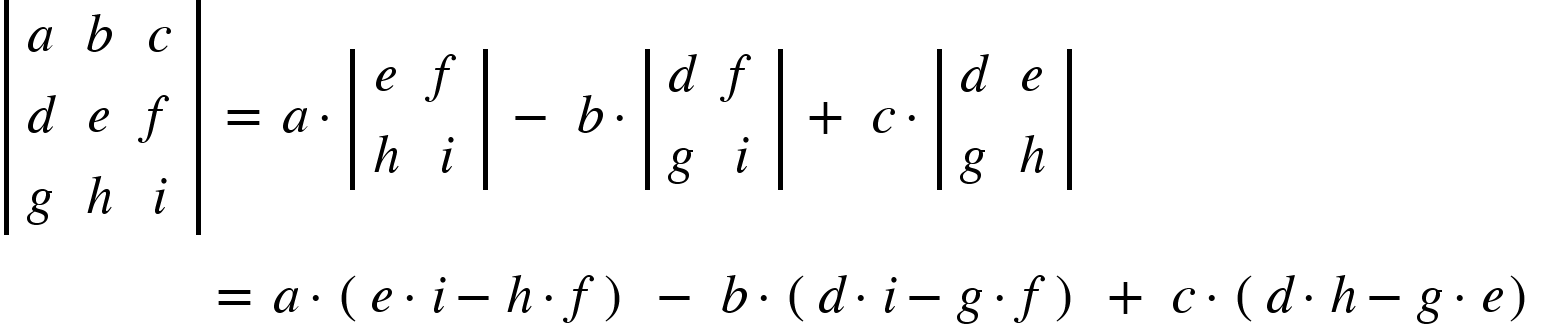
Note: We will put alternating + and - signs.
Examples:
a.)
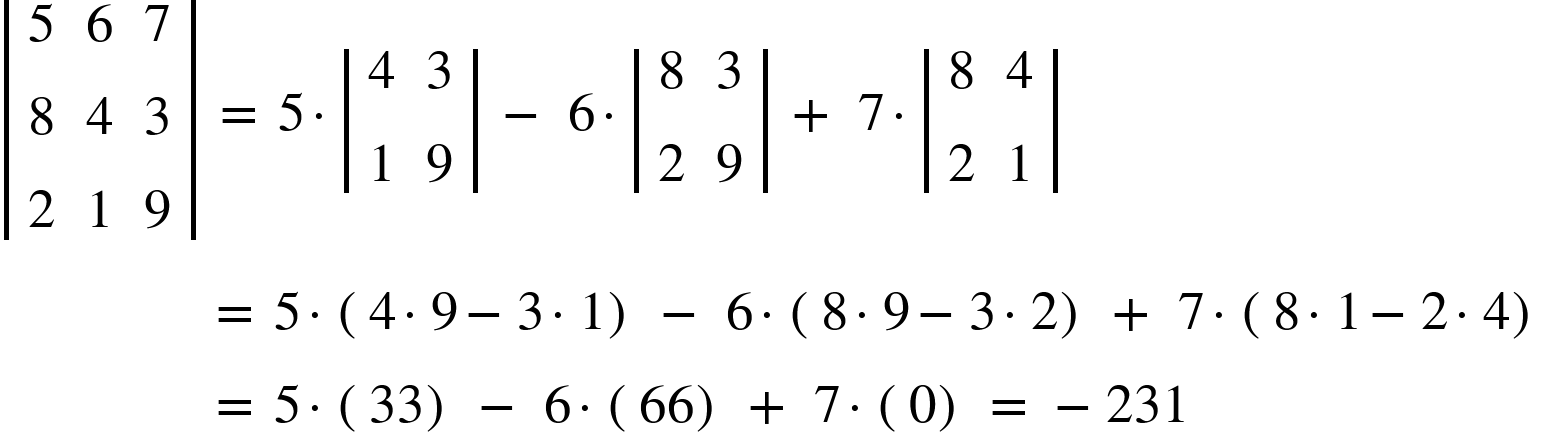
b.)
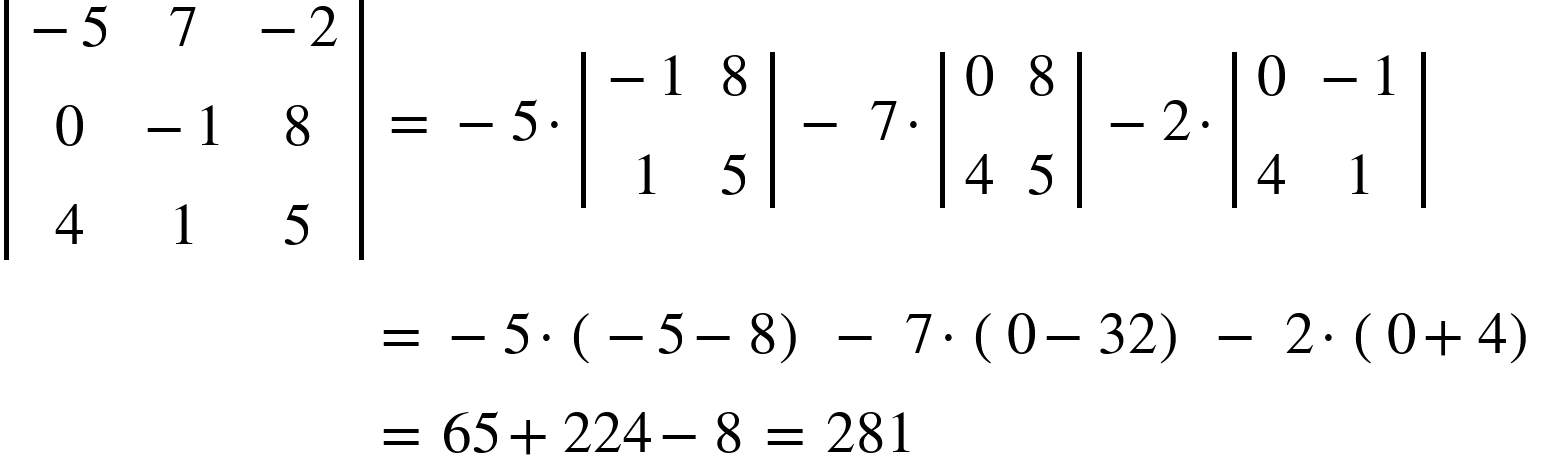
Evaluation of 4th Order Determinant
A 4th-order or  the determinant can be written as:
the determinant can be written as:

It can be evaluated using third-order determinants. Again, be careful about the alternating plus and minus sign.
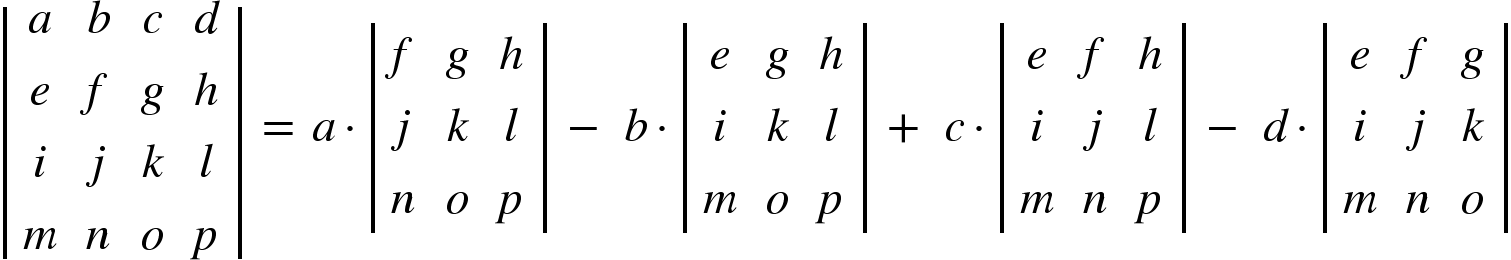
Using the method we learned previously, we can easily calculate the value of these 3rd order determinants generated in the above equation.
Example:
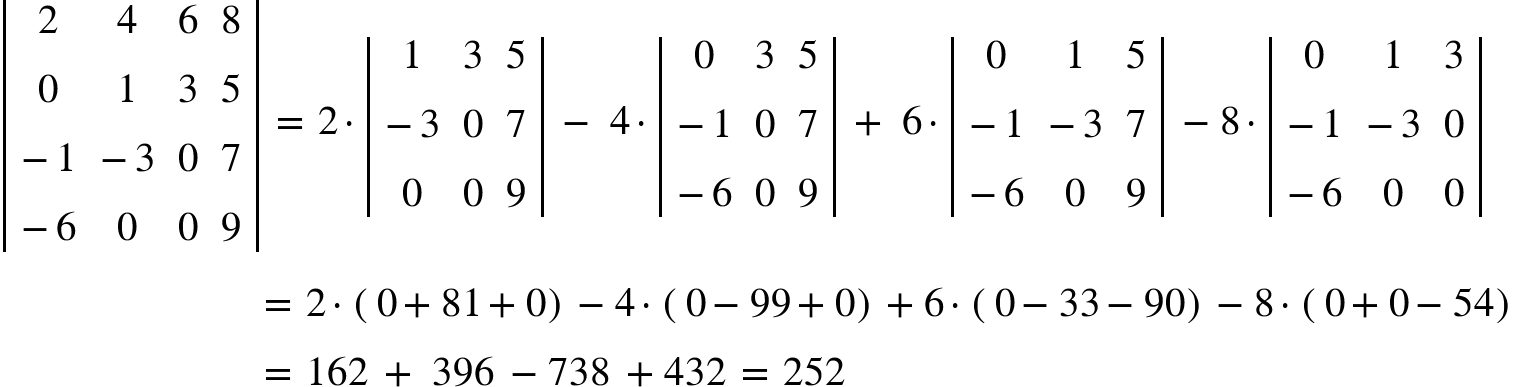
Properties of Determinants
Some of the valuable properties of determinants are:-
1.) The determinant's value remains unchanged if the rows and columns are interchanged.
2.) If any two rows or columns of a determinant are interchanged, the sign of the determinant changes.
3.) The determinant is 0 if any two rows or columns of the determinant are the same.
4.) If a variable k is multiplied by any row or column of the determinant, its value is multiplied by k.
5.) If some or all row or column elements can be expressed as the sum of two or more terms, then determinants can also be expressed as the sum of two or more determinants.
FAQs
1. What is Determinant?
A determinant is a scalar value evaluated from the elements of a square matrix.
They are an arrangement of numbers in the form.
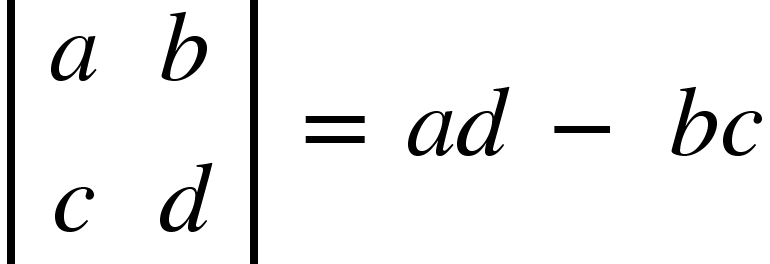
2. List some applications of Determinants.
Some of the applications of determinants are; we can use them to solve simultaneous equations and evaluate vector products.
3. If any two rows or columns of a determinant are the same, how to calculate the value of the determinant
The value of the determinant is 0 if any two rows or columns of the determinant are the same.
Key Takeaways
In this article, we have extensively discussed the Determinants, evaluation of determinants, and different properties of determinants.
We hope that this blog has helped you enhance your knowledge regarding Linear Algebra. If you want to learn more, check out our articles on the Matrix and Types of Matrix.
Check out this problem - Matrix Median
Do upvote our blog to help other ninjas grow.
Happy Learning!
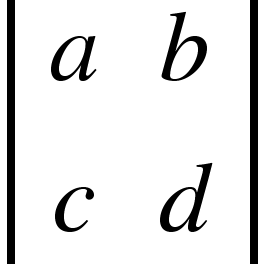 .
. as a determinant of order 2, and the four numbers arranged in row and column are called elements of determinant. In a determinant, horizontal lines are rows, and vertical lines are called columns. The shape of every determinant is a square.
as a determinant of order 2, and the four numbers arranged in row and column are called elements of determinant. In a determinant, horizontal lines are rows, and vertical lines are called columns. The shape of every determinant is a square. 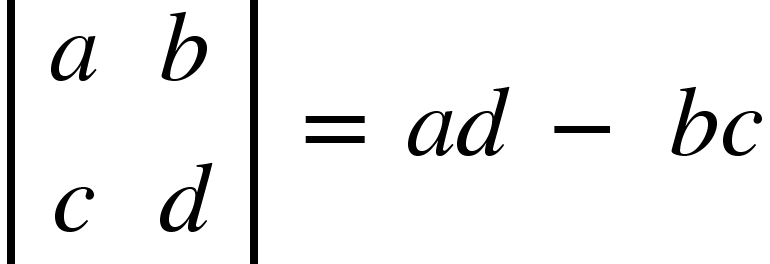
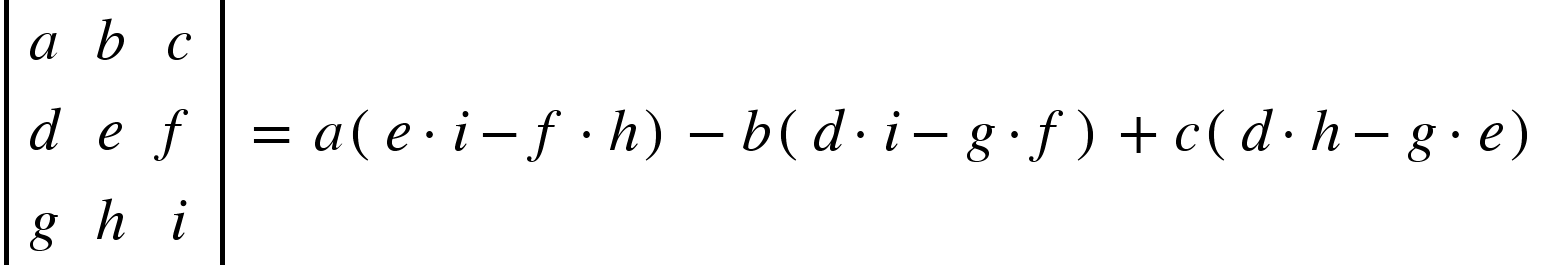
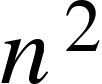 .
.