Introduction
Before beginning with this question, let’s recap what a graph means.
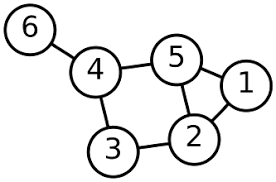
A graph is a data structure that is not linear and contains edges that connect vertices.
Graphs can be either directed or undirected. A directed graph is a collection of vertices/nodes connected by edges where each edge has a direction. The edges of the graph are indicated by arrows pointing in the direction of traversal. If an arrow is pointing towards 2 on edge between vertex 1 and 2, the graph can be traversed from 1 to 2 rather than 2 to 1. On the other hand, an undirected graph can be traversed in either direction, i.e., we can travel in the graph from 1 to 2 and 2 to 1 if the graph is undirected.
Problem Statement
We are given a graph with (N+1) nodes and a boolean array of size N. There will be in total (2*N-1) edges where:
- (N-1) edges will be from ith node to (i+1)th node and
- The rest of N edges will be from ith node to (N+1)th node if booleanArray[i] = 0; otherwise, edge will be from (n+1)th to ith node.
You have to find whether a path that can visit all the nodes will exist or not, and if the path exists, print the path.
Example 1:
Input: N = 3 booleanArray[] = {0, 1, 0}
The Tree for the above input will be:
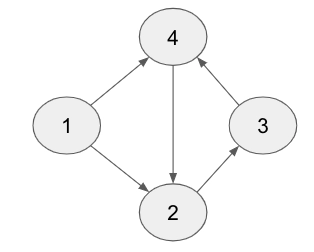
Output: [1,2,3,4]
Example 2:
Input: N = 4 booleanArray[] = {0, 1, 1, 1}
The Tree for the above input will be:
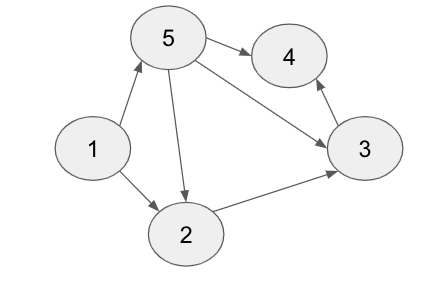
Output: [1,5,2,3,4]





