Introduction
DFA minimization is the process of converting a DFA D into its equivalent DFA D’ (where ‘D’ is the input DFA and ‘D’’ is the output DFA such that:
- If D accepts a string, D’ will also accept that string.
- If D rejects a string, D’ will also reject a string.
- D’ has the minimum number of states.
Also See, Moore Machine
Procedure
Let the given DFA be D(Q, Σ, q0, δ, F). The output of DFA minimization D’(Q’, Σ, q0, δ’, F’) can be created by compressing equivalent states. Two states (p, q) are called equivalent if for every string w, either {δ(p, w), δ(q, w)} belongs to F or does not belong to F. We can find equivalent states using the following:
- Remove all the states that are unreachable from the initial start state.
- Create a table of pairs (p, q) where p, q denotes some two states of Q. Initially, all the table cells are unmarked.
- Mark all the pairs (p, q) such that p belongs to F and q does not belong to F, or vice versa.
- If (p, q) is unmarked and there exists a symbol such that {δ(p, a), δ(q, a)} is marked, then mark p and q.
- Repeat step-4 until no new pairs get marked.
- After completing the above process, p is equivalent to q if and only if (p, q) is unmarked. The equivalent states can be compressed to get the minimum number of states.
After this, we will just compress the equivalent states into a single state to get the DFA with the minimum number of states. The above DFA minimization algorithm is called Moore’s Algorithm.
Read About - Simplification of CFG
Example of DFA Minimization
Consider the following DFA:
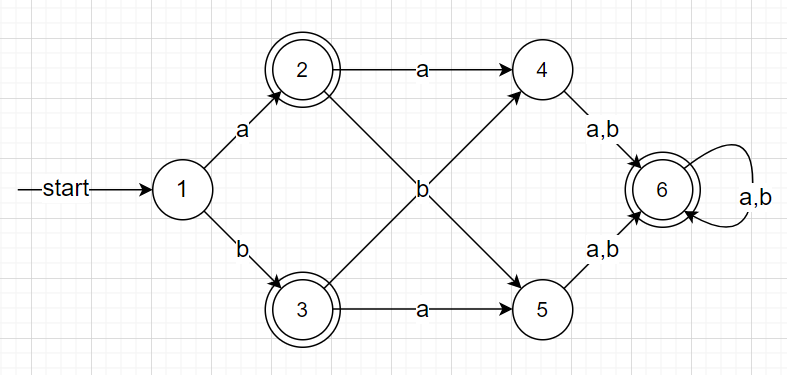
To do DFA minimization, we will create a table of pairs to mark and unmark them. Now mark the states (p, q) if p belongs to F and q does not belong to F or vice versa.
For example,
- 1 does not belong to the final state while 2 belongs to the final state. Therefore we mark (1, 2).
- 1 does not belong to the final state, while 3 belongs to the final state. Therefore we mark (1, 3).
- 2 and 3 belong to the final state, so we don’t mark (2, 3) yet.
Similarly, we will check for every pair of states. The table after performing this step will look like:
| 1 | |||||
| X | 2 | ||||
| X | 3 | ||||
| X | X | 4 | |||
| X | X | 5 | |||
| X | X | X | 6 |
Now, we will check if there exist two states p and q such that (p, q) is unmarked and there exists a symbol such that {δ(p, a), δ(q, a)} is marked, then mark p and q. We have to perform this until no new pairs (p, q) get marked.
For example,
- δ(2, ‘a’) is 4, which is not in the final state, while δ(6, ‘a’) is 6, which is in the final state. Therefore, we will mark (2, 6).
- δ(3, ‘a’) is 5, which is not in the final state, while δ(6, ‘a’) is 6, which is in the final state. Therefore, we mark (3, 6).
- δ(2, ‘a’) is 4 and δ(3, ‘a’) is 5, both are not in the final state Therefore, we left them unmarked.
Similarly, check for every unmarked pair of states until no new pairs get marked.
Table after 1st iteration:
| 1 | |||||
| X | 2 | ||||
| X | 3 | ||||
| X | X | 4 | |||
| X | X | 5 | |||
| X | X | X | X | X | 6 |
Table after 2nd iteration:
| 1 | |||||
| X | 2 | ||||
| X | 3 | ||||
| X | X | X | 4 | ||
| X | X | X | 5 | ||
| X | X | X | X | X | 6 |
No more pairs can be marked any further, hence the algorithm terminates. From the final table, we can see that the states (2, 3) and (4, 5) are equivalent. Hence, the DFA with the minimum number of states can be formed by compressing these states. The output of the DFA minimization will have the following form:
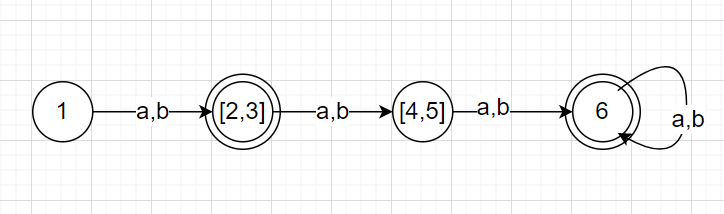
The minimum number of states here is 4.
Also see, Turing Machine in TOC.




