Introduction
In this blog, we are provided with a binary tree problem. The task is to find the sum of all the diagonal elements of the respective binary tree. Before moving further, please take note that all of the right branches are drawn parallel to one another, and the same is true for all of the left branches.
Now, let's understand what we have to implement in the problem statement:
Problem Statement
Determine the sum of all nodes for each diagonal with a negative slope given a binary tree. Assume that a node's left and right children are at a 45-degree angle with the parent.
Sample Examples
Example 1:
Here for the input tree,
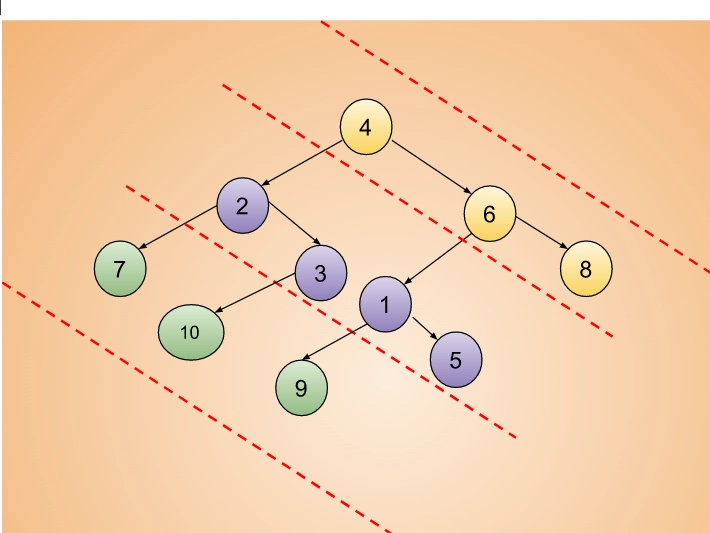
Output:
18 11 26
Explanation:
As we see in the diagram,
Sum of 4, 6 and 8 = 18
Sum of 2, 3, 1,and 5= 11
Sum of 7, 10 and 9 = 26
Example 2:
Here for the input tree,
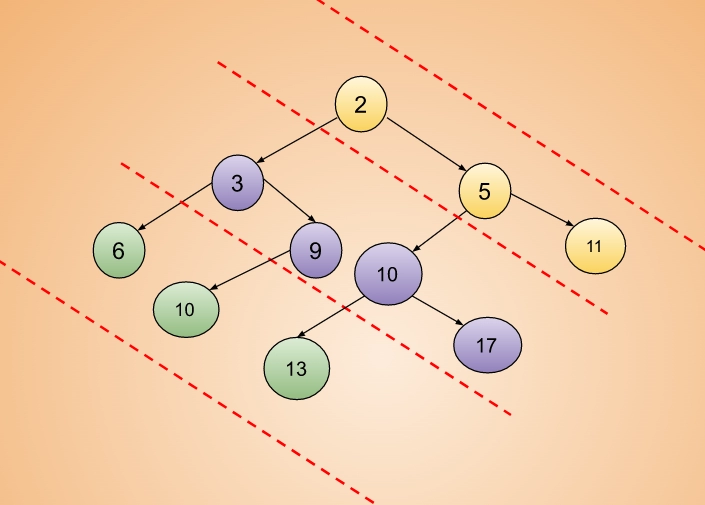
Output:
18 39 29Explanation:
As we see in the diagram,
Sum of 2, 5 and 11 = 18
Sum of 3, 9,10, and 17= 39
Sum of 6, 10 and 13= 29Approach1
With the aid of hashing, we can quickly resolve this problem. The goal is to construct an empty map, where each key corresponds to a binary tree diagonal and each value maintains the total number of nodes that make up the diagonal. Then update the map after preorder traversal of the tree. Increase the diagonal by one for each node's left subtree and repeat with the same diagonal for each node's right subtree.
Algorithm
-
Establish a data structure to hold a binary tree node.
-
Construct a recursive function to preorder traverse the tree and fill the map with the diagonal sum of the elements.
-
Update the current diagonal with the value of the node
-
Repeat with the diagonal raised by 1 for the left subtree.
-
Repeat for the right subtree along the identical diagonal
-
Create a function that prints the diagonal sum of a binary tree
-
Make an empty map and enter the diagonal sum for each slope in it.
-
Fill the map by traversing the tree in a preorder fashion
- Traverse the map and print the diagonal sum.
Implementation
#include <iostream>
#include <unordered_map>
using namespace std;
struct Node
{
int data;
Node *left, *right;
Node(int data)
{
this->data = data;
this->left = this->right = nullptr;
}
};
void diagonalSum(Node* root, int diagonal, auto &map)
{ if (root == nullptr) {
return;
}
map[diagonal] += root->data;
diagonalSum(root->left, diagonal + 1, map);
diagonalSum(root->right, diagonal, map);
}
void diagonalSum(Node* root)
{
unordered_map<int, int> map;
diagonalSum(root, 0, map);
for (int i = 0; i < map.size(); i++) {
cout << map[i] << " ";
}
}
int main()
{
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->left = new Node(5);
root->right->right = new Node(6);
root->right->left->left = new Node(7);
root->right->left->right = new Node(8);
diagonalSum(root);
return 0;
}
Output:
10 15 11
Complexity Analysis
Time Complexity: O(n), As the given program requires preorder traversal of the binary tree. So, the time complexity is O(n). As the input grows, the algorithm takes proportionally longer to complete.
Space Complexity: O(n) As the given program contains a map, linear space complexity occurs.




