Introduction
Today, let's learn about a famous and commonly asked Interview Problem, i.e., the Diagonal Traversal of a Binary Tree.
So, Binary Tree is a generic tree with only two children, i.e., left and right. And Diagonal Traversal of a Binary Tree here means that we need to traverse diagonally by diagonal and print all the nodes occurring in a diagonal.
Problem Statement: Given the root of the binary tree, we need to return the diagonal traversal(lines of slope -1) of its nodes' values.
Example:
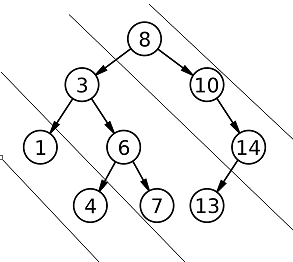
Let's divide the entire Binary Tree into diagonals(slopes of lines -1). Now, traversing along diagonals, we print all the nodes we encounter.
So,
Nodes that lie along the Diagonal
On Diagonal 1 - 8 10 14
On Diagonal 2 - 3 6 7 13
On Diagonal 3 - 1 4
So, the Diagonal Traversal of the given Binary Tree would be: 8 10 14 3 6 7 13 1 4
There is both a recursive and an iterative approach to printing the Diagonal Traversal of a Given Binary Tree. Let's discuss both of them in detail.
Recommended: Try the Problem yourself before moving on to the solution.
Approach 1 - Iterative Approach
Here, we start by printing our current node and adding a NULL in our queue. We use a queue data structure to store the current node's left child and move our pointer to the right child of the node.
We continue this process till the right child exists. Once the process ends, we look for the nodes in the queue. If the queue stores a NOT NULL node, we continue the same process. However, if it's a NULL node, it acts as a delimiter, guiding us that the incoming nodes now are of new diagonal and hence have to be printed in a new line. We pop this NULL node and add another NULL node in the queue at the same time if the size of the queue is non-zero after popping the NULL node indicating the presence of the next diagonal.
Let us look at an example to get a more clear picture of the above algorithm.
Example :
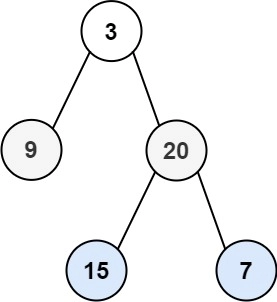
Initially Output displays [3] i.e. the root’s data and queue stores [NULL] node.
Now, the process starts for the root node.
Its left child is entered in the queue and the pointer to the current node points to the right child.
Print/Output Screen Queue
Step1: 3 [NULL, 9] ---> Pointer now moves to 20
Step2: 3 20 [NULL, 9,15] ---> Pointer now moves to 7
Step3: 3 20 7 [NULL, 9,15] ---> Pointer now moves to NULL
Since, the current node is NULL now, the inner while loop breaks, and NULL (first element of queue is popped out).
Since, the popped element = NULL, a new line is printed hence starting with a new diagonal. Also, NULL is entered in the queue.
Step4: 3 20 7 [9,15,NULL]
Step5: 3 20 7
9 [15, NULL] ---> Pointer now moves to 9
Step6: 3 20 7
9 15 [NULL] ---> Pointer now moves to 15
Implementation
Let’s have a look at its implementation in Java
import java.util.*;
import java.lang.*;
import java.io.*;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public static void diagonalTraversal(TreeNode root) {
// edge case
if (root == null)
return;
// using queue of Treenode
Queue<TreeNode> q = new LinkedList<>();
// adding root and NULL delimiter in queue
q.add(root);
q.add(null);
while (q.size()>0) {
TreeNode temp = q.peek();
q.remove();
// if current node is NULL,
//insert another NULL for next diagonal
if (temp == null) {
// if queue is empty return
if (q.size()==0)
return;
System.out.println();
// Adding another delimiter
q.add(null);
}
else {
while (temp!=null) {
System.out.print( temp.val + " ");
// add left child of current node in queue
if (temp.left!=null)
q.add(temp.left);
// Moving temp to right child of current node
temp = temp.right;
}
}
}
}
public static void main (String[] args) {
Scanner s = new Scanner(System.in);
System.out.println("Form a tree: ");
TreeNode root = new TreeNode(s.nextInt());
root.left = new TreeNode(s.nextInt());
root.right = new TreeNode(s.nextInt());
root.right.left = new TreeNode(s.nextInt());
root.right.right = new TreeNode(s.nextInt());
System.out.println("Diagonal Traversal of Binary Tree ");
diagonalTraversal(root);
}
}
Output:
|
Form a tree: 3 9 20 15 7 3 20 7 9 15 |
Time and Space Complexity
Time Complexity: O(n) as we are traversing all the nodes of the Binary tree in Diagonal traversal of the Binary Tree at least once.
Space Complexity: O(n) as extra space for storing the left child of the current nodes in a queue, where n is the number of nodes in the Binary Tree.
Read More - Time Complexity of Sorting Algorithms





