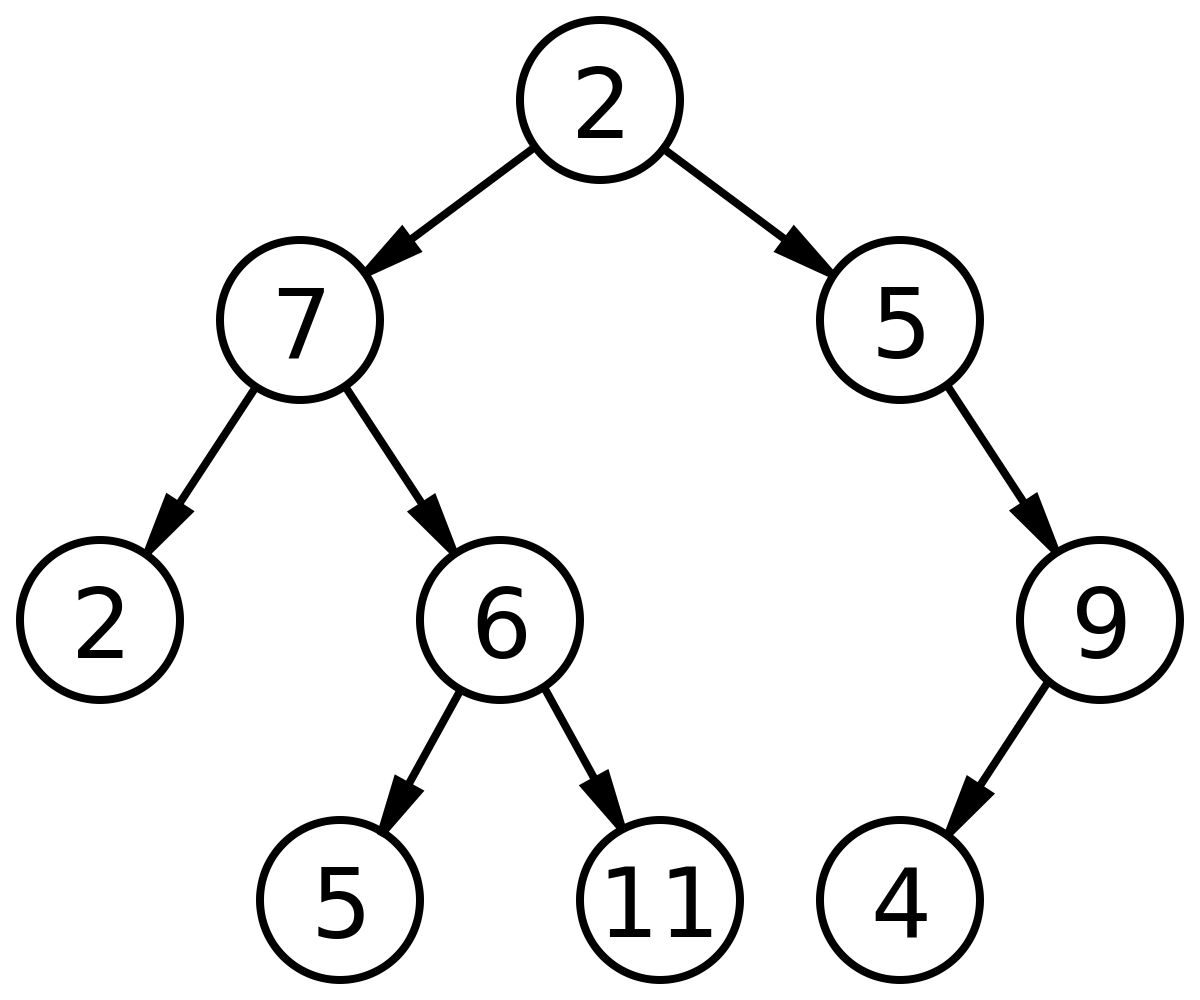
What is the diameter of a binary tree?
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root. The number of edges between them represents the length of a path between two nodes.
We can see the two cases discussed down below in the image:
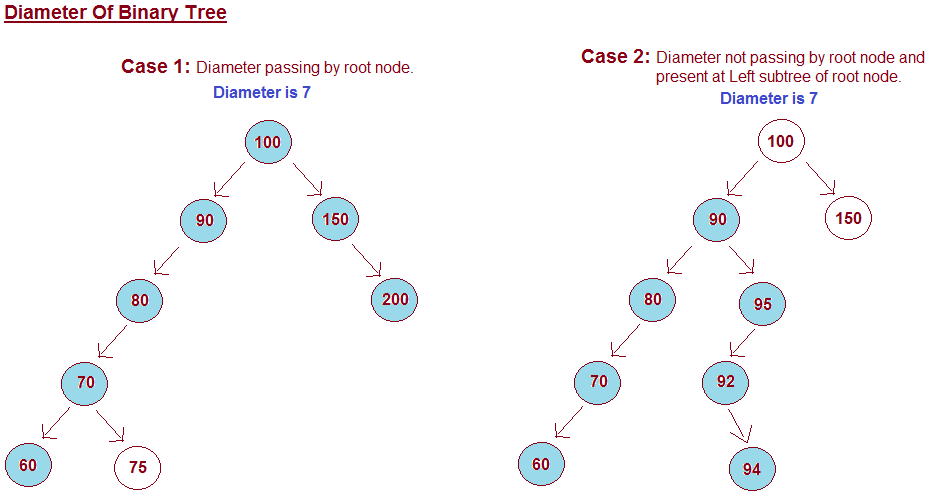
Algorithm for finding the diameter of binary tree
The idea is to find the diameter of the binary tree and as by the definition we got to know diameter is the farthest distance between two nodes. So some people also mistook this by thinking that diameter is nothing but the sum of the height of the left subtree and right subtree. But it’s not the case that we saw in case 2 of the above image.
So how are we going to do it?
- Find the height of the left subtree
- Find the height of the right subtree
- Find the left diameter and right diameter
- Then diameter is the maximum sum of the height of the left subtree plus the height of the right subtree, the left diameter, and the right diameter. E.g. max( lh+rh,max(ld,rd))
Diameter of binary tree implementation in C++
Here in the implementation part, we are going to discuss the two approaches for finding the diameter of a binary tree:
Brute force approach
#include <iostream>
#include <queue>
using namespace std;
template <typename T>
class BinaryTreeNode {
public:
T data;
BinaryTreeNode<T>* left;
BinaryTreeNode<T>* right;
BinaryTreeNode(T data) {
this->data = data;
left = NULL;
right = NULL;
}
};
//calculating the height of a binary tree
int height(BinaryTreeNode<int>* root) {
if (root == NULL) {
return 0;
}
return 1 + max(height(root->left), height(root->right));
}
int diameter(BinaryTreeNode<int>* root) {
//if the tree is empty
if (root == NULL) {
return 0;
}
// finding sum of the height of left subtree and right subtree
int option1 = height(root->left) + height(root->right);
// calculating the diameter of left subtree
int option2 = diameter(root->left);
// calculating the diameter of right subtree
int option3 = diameter(root->right);
// return the maximum of all the three options
return max(option1, max(option2, option3));
}
//taking input level-wise
BinaryTreeNode<int>* takeInput() {
int rootData;
cin >> rootData;
if (rootData == -1) {
return NULL;
}
BinaryTreeNode<int>* root = new BinaryTreeNode<int>(rootData);
queue<BinaryTreeNode<int>*> q;
q.push(root);
while (!q.empty()) {
BinaryTreeNode<int>* currentNode = q.front();
q.pop();
int leftChild, rightChild;
cin >> leftChild;
if (leftChild != -1) {
BinaryTreeNode<int>* leftNode = new BinaryTreeNode<int>(leftChild);
currentNode->left = leftNode;
q.push(leftNode);
}
cin >> rightChild;
if (rightChild != -1) {
BinaryTreeNode<int>* rightNode =
new BinaryTreeNode<int>(rightChild);
currentNode->right = rightNode;
q.push(rightNode);
}
}
return root;
}
int main() {
BinaryTreeNode<int>* root = takeInput();
cout << diameter(root);
}

You can also try this code with Online C++ Compiler
Input:
The first and the only line of input will contain the node’s data, all separated by a single space. Since -1 is used to indicate whether the left or right node data exist for root, it will not be a part of the node data.
1 2 3 4 5 6 7 -1 -1 -1 -1 -1 -1 -1 -1
Output:
4
Time Complexity: The time complexity in the worst case is O (N^2), where N is the number of nodes in the tree, and for each node, we have to calculate the height of the left subtree and right subtree and then again left diameter and right diameter. The time complexity on average will be O(N*logN) when the given tree is balanced.
Space complexity: Space complexity is O(1) as we are not using any other data structure.
Explanation of worst-case time complexity of O(N^2)
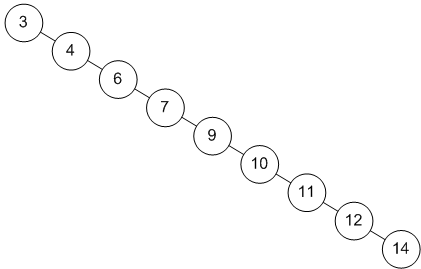
As we can see above is a skewed tree, A skewed binary tree is a binary tree in which all of the nodes have only one or no children, and the worst time taken for the tree is O(N^2) which is similar to bubble sort, so the recurrence relation for this is:
For each iteration of the outer loop, we place the largest element at the end of the array. In simple words, the ith iteration of the outer loop moves the largest element from the first N-i elements to (N-i-1)th position.
T(n)=T(n−1)+(n−1).
N is the number of steps required to place the largest element at the end of the array, and T(N-1) signifies the time needed to sort the rest of the N-1 elements.
Explanation of time complexity of O(N*logN) in the average case
The average-case time complexity is O(nlogn) as you can see in the image below for such a balanced binary tree.
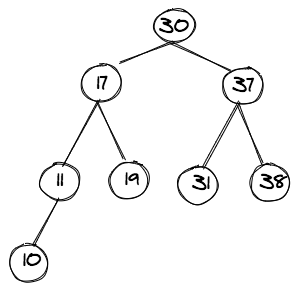
A balanced binary tree, also known as a height-balanced binary tree, as it is a binary tree in which the height of each node's left and right subtree differs by no more than one, and the worst time taken by the such tree is O(nlogn) which is similar to merge sort.
So the recurrence relation for this is:
On each call of merge_sort, we split the array into two equal parts. Then we recursively sort the two parts. After sorting the two halves, we merge them such that the array remains sorted.
T(n) = 2T(n/2) + O(n)
2*T(N/2) is the time required to sort the two equal parts of the array. N is the time required to merge the two sorted parts into a single sorted array.
So we can say overall, our solution has a time complexity of O (n* height of binary tree). When our tree is a balanced binary tree then it has a height of logn, so the time complexity becomes O (nlogn), and when our tree is skewed, then the height of the tree is equal to the total number of nodes present in the tree, so the time complexity is O (n^2).
Optimized approach
In this approach, we are going to optimize our previous solution as in the method discussed above, we were calculating the height first and then the diameter. So, here we will implement our function in such a way that one recursion call will get us the diameter as well as the height of both the left subtree and the right subtree for each node of the tree.
Let’s see the code discussed below:
#include <iostream>
#include <queue>
using namespace std;
template <typename T>
class BinaryTreeNode {
public:
T data;
BinaryTreeNode<T>* left;
BinaryTreeNode<T>* right;
BinaryTreeNode(T data) {
this->data = data;
left = NULL;
right = NULL;
}
};
// Helper function for calculating diameter of binary tree
pair < int, int > heightDiameterHelper(BinaryTreeNode<int>* root) {
//if the given tree is empty or we reach end of root
if (root == NULL) {
//this pair will going to store both height and diameter
pair < int, int > p;
p.first = 0; //height
p.second = 0; //diameter
return p;
}
//we made two recursive calls for left subtree and right subtree
pair < int, int > leftAns = heightDiameterHelper(root->left);
pair<int, int> rightAns = heightDiameterHelper(root->right);
int ld = leftAns.second; //left diameter
int lh = leftAns.first; //left height
int rd = rightAns.second; //right diameter
int rh = rightAns.first; //right height
//height will be 1 plus maximum of left height & right height
int height = 1 + max(lh, rh);
//diameter will be max among left diameter, right diameter and sum of left height plus right height
int diameter = max(lh + rh, max(ld, rd));
//then making a pair and storing the height and diameter in it
pair < int, int > p;
p.first = height;
p.second = diameter;
return p;
}
//function for calculating diameter of binary tree
int diameter(BinaryTreeNode<int>* root) {
return heightDiameterHelper(root).second;
}
//taking input level-wise
BinaryTreeNode<int>* takeInput() {
int rootData;
cin >> rootData;
if (rootData == -1) {
return NULL;
}
BinaryTreeNode<int>* root = new BinaryTreeNode<int>(rootData);
queue<BinaryTreeNode<int>*> q;
q.push(root);
while (!q.empty()) {
BinaryTreeNode<int>* currentNode = q.front();
q.pop();
int leftChild, rightChild;
cin >> leftChild;
if (leftChild != -1) {
BinaryTreeNode<int>* leftNode = new BinaryTreeNode<int>(leftChild);
currentNode->left = leftNode;
q.push(leftNode);
}
cin >> rightChild;
if (rightChild != -1) {
BinaryTreeNode<int>* rightNode =
new BinaryTreeNode<int>(rightChild);
currentNode->right = rightNode;
q.push(rightNode);
}
}
return root;
}
int main() {
BinaryTreeNode<int>* root = takeInput();
cout << diameter(root);
}

You can also try this code with Online C++ Compiler
Input:
The first and the only line of input will contain the node’s data, all separated by a single space. Since -1 is used to indicate whether the left or right node data exist for root, it will not be a part of the node data.
1 2 3 4 5 6 7 -1 -1 -1 -1 -1 -1 -1 -1
Output:
4
Time Complexity: Time complexity is O (n) as we are not iterating any node twice, and in each recursion call, it’s giving us both the diameter and height.
Space complexity: Space complexity is O(1) as we are not using any other data structure.
Frequently Asked Questions
What is the pseudocode for finding the height of a binary tree?
- The height of a binary tree is 1 + max of the left subtree and right subtree. Considering the height of the root node is 1, we add 1 in the result.
-
In the case of a null tree, the height is 0.
int height(BinaryTreeNode<int>* root) {
if (root == NULL) {
return 0;
}
return 1 + max(height(root->left), height(root->right));
}

You can also try this code with Online C++ Compiler
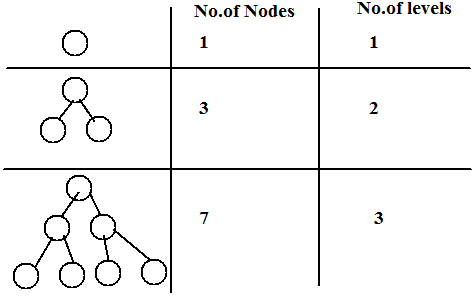
What is the maximum no. of nodes in a binary tree with height h?
The maximum no. of nodes in a binary tree with height h is 2h-1.
Conclusion
This article discussed how to find the diameter of a binary tree with all crucial aspects. We discussed the binary Tree and its diameter and implemented the two approaches in the C++ programming language.
Recommended Reading:
Do check out The Interview guide for Product Based Companies as well as some of the Popular Interview Problems from Top companies like Amazon, Adobe, Google, Uber, Microsoft, etc. on Coding Ninjas Studio.
Also check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, DBMS, System Design, etc. as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.
Cheers!