Table of contents

Introduction

Trie Operations:

Implementation of Dictionaries using Tries

3.1.

Output:

3.2.

3.3.

3.4.

Time Complexity

3.5.

Space Complexity

Other Applications of Tries

Practice Problems:

Key Takeaways:

Last Updated: Mar 27, 2024

Dictionaries using Tries

Author Hussain Kagdi

Introduction

Abbas and Hatim were two friends who lived in Yemen. Once, they visited India to see the Taj Mahal. However, they were not able to understand Hindi since they only understood Arabic. So they tried to create their dictionary software. “How would we implement this dictionary, Hatim?” asked Abbas. “Should we use a hashmap?” No, Hatim said, we will implement our dictionary using tries.

Abbas wondered, “What in the world is a trie?” Hatim then explained the concept of tries to Abbas.

Trie is a tree-based data structure used to store words in a dictionary. Let us consider that the number of letters in the English language is twenty-six if we only consider lowercase letters. Then each node of a trie will contain a character of the word and will contain a children array. It can have a maximum of 26 children.

Consider the below given example.

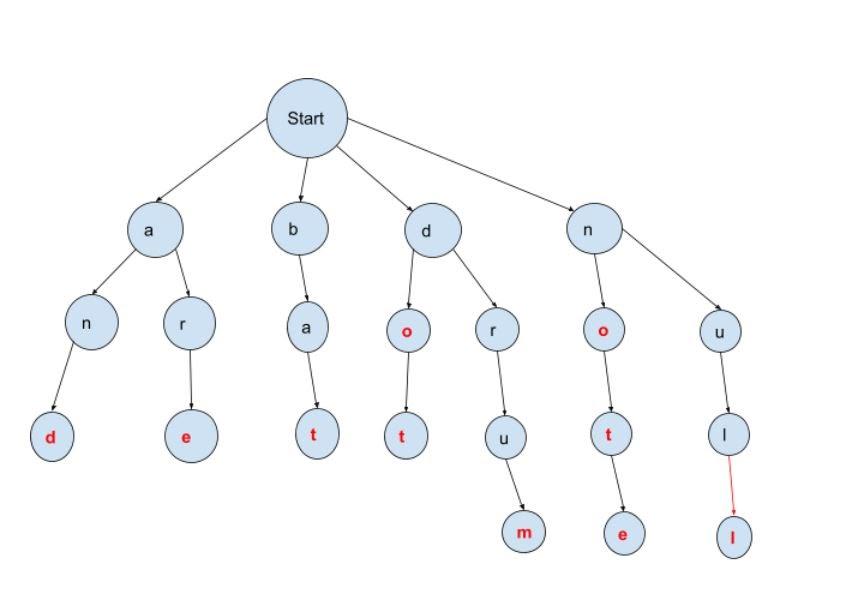
The words that we have stored in the above trie are as follows:

And, Are, Bat, Do, Dot, Drum, No, Not, Note, Null.

Please note that by storing words in a trie, we can save a lot of space. For example, if 10000 words start with the character ‘a’, we store it just one time. Again if 1000 words start with “ba,” then we are storing it just once. Thus it saves a lot of space for us.

Trie Operations:

Let us continue with our previous example.

Insert: Suppose we want to insert the word “Cricket” in the above trie. First, we will check if the start node has a child with the value ‘C’.

If the start node doesn’t contain the first character of the word, this means there is no word starting with ‘C’. So will attach the entire word in the trie. To do this, first, we will make ‘C’ as a child of the root node, then ‘r’ as a child of ‘C’, then ‘i’ as the child of ‘r’, and so on. Finally, we will mark ‘t’ as a terminal node to mark it as the end of the word. That is why we will mark it red.
Else if the start node contains the character ‘C’, we will match each character one by one until we get the first mismatch. Then we will attach the remaining word from that node.

If the trie contained the word “Crack”, then we will traverse till node ‘r’ and then attach “icket” to the subtree of ‘r’.

Finally, when the entire word is inserted we attach the meaning of the word in

the node representing the last character.

Search: Suppose we want to search the word “null” in the above trie-based dictionary. First, we will check whether the start node contains the first character ‘n’ as a child node. If not, it means that the word ‘null’ is not present in the trie.

If yes, we will move to the child node of ‘n’ and search the remaining word recursively. We will check whether ‘u’ is a child of ‘n’ and ‘l’ is a sub child of ‘u’ and so on. Finally, when we reach the last character of the word, we will check if it is marked as terminal or not. If yes, then we return the meaning of the word, else the word does not exist in the trie.

Let us now see the dictionary implementation using tries.

Implementation of Dictionaries using Tries

#include <bits/stdc++.h>
using namespace std;

class TrieNode
{
public:

    // Data Members of TrieNode class.
  char data;
TrieNode **children;
  bool isTerminal;
  string meaning;

TrieNode(char data, string meaning)
{

        // Initializing the data members.
  this->data = data;
children = new TrieNode *[26];
  for (int i = 0; i < 26; i++)
{
children[i] = NULL;
}
isTerminal = false;
  this->meaning = meaning;
}
};

class Trie
{
TrieNode *root;

public:
  int count;

Trie()
{
  this->count = 0;
root = new TrieNode('\0', "");
}

  bool insertHelper(TrieNode *root, string word, string meaning)
{
  // Base case.
  if (word.size() == 0)
{
  if (!root->isTerminal)
{

// Reached the end of word.
root->isTerminal = true;

                // Attaching meaning of word.
root->meaning = meaning;
  return true;
}
  else
{
  return false;
}
}

  int index = word[0] - 'a';
TrieNode *child;

        // Checking if character exists or not
  if (root->children[index] != NULL)
{
child = root->children[index];
}
  else
{
child = new TrieNode(word[0], meaning);
root->children[index] = child;
}

  // Recursive call to attach the rest of the word.
  return insertHelper(child, word.substr(1), meaning);
}

  void insertWord(string word, string meaning)
{
  if (insertHelper(root, word, meaning))
{
  this->count++;
}
}

  string searchHelper(TrieNode *root, string patt)
{
  if (patt.size() == 0){

// Word found. So return meaning.
return root->meaning;

        }
  int index = patt[0] - 'a';
  if (root->children[index] == NULL)
{

// Word not found. So return an empty string.
return "";
}

        // Recursive call.
  return searchHelper(root->children[index], patt.substr(1));
}

  string search(string word)
{
  return searchHelper(root, word);
}
};

int main()
{
Trie *dictionary = new Trie();
dictionary->insertWord("are", "It is a verb");
dictionary->insertWord("and", "It is a conjunction");
dictionary->insertWord("do", "To perform a task");
dictionary->insertWord("dot", "A point of any colour");
dictionary->insertWord("cricket", "A game introduced by Britishers");
dictionary->insertWord("null", "similar to void");
dictionary->insertWord("note", "A document to store something");
dictionary->insertWord("bat", "A cricket accessory made of wood");
dictionary->insertWord("drum", "Musical instrument");

  cout << "Meaning of cricket: " << dictionary->search("cricket") << '\n';
  cout << "Meaning of and: " << dictionary->search("and");
  return 0;
}

Output:

Meaning of cricket: A game introduced by Britishers

Meaning of and: It is a conjunction

Time Complexity

The time complexity of all the three functions insert() and search() is O(N), where ‘N’ is the length of the word. It is because in every case we are traversing through the entire word.

Space Complexity

O(26 * N), where N is the number of words.

Other Applications of Tries

Here are some other interesting applications of tries apart from building a dictionary.

AutoComplete: It is one of the most important applications of tries. It is a mechanism in which the software guesses the remaining part of the word the user is typing based on the string prefix.

Spell Checker/ Autocorrect: Spell checking or Autocorrect is a three-step process.
Check for the word in the trie.
Generate potential suggestions
Sort the suggestions with the highest priority first.

3) Longest Prefix Matching: Longest prefix matching is an algorithm used by routing devices in IP networking.

Practice Problems:

Would you mind moving to our coding platform, Coding Ninjas Studio, and practice some coding problems on tries. After implementing them you will be a Ninja in tries.

Key Takeaways:

In this blog, we learned about a new data structure called Tries. And how to implement dictionaries using tries. We can implement dictionaries very efficiently using tries. We learned how to insert, search and delete a word in a trie and learned how to implement it in C++. Next, we saw some of its exciting applications. Practising these problems would increase your proficiency in data structures.

Also check out - Data Dictionary In Software Engineering

Thank you and Happy Coding.

By: Husen Kagdi

Live masterclass

IIT Online PG Certification: Useful for data career?

by Coding Ninjas

07 Jan, 2025

01:30 PM

51+ registered

IITG FSD TEST

by Saurav Prateek, SDE2@Google

05 Jan, 2025

01:30 PM

2+ registered

IIT Online certifications: Helps in placements for SDE roles?

by Coding Ninjas

06 Jan, 2025

03:30 PM

447+ registered

Google Finance Analyst roadmap: Essential SQL concepts

by Maaheen Jaiswal, Data Analyst @ Google

06 Jan, 2025

01:30 PM

766+ registered

IIT Online PG Certification: Useful for data career?

by Coding Ninjas

07 Jan, 2025

01:30 PM

51+ registered

IITG FSD TEST

by Saurav Prateek, SDE2@Google

05 Jan, 2025

01:30 PM

2+ registered

View more events