Table of contents

Introduction

Backpropagation

Stochastic Gradient Descent

3.1.

Steps for Stochastic gradient descent

3.2.

Difference between backpropagation and stochastic gradient descent.

FAQs

Key Takeaways

Last Updated: Mar 27, 2024

Difference Between Backpropagation and Stochastic Gradient Descent

Author soham Medewar

Introduction

While training the neural network, everyone might encounter the two terms backpropagation and stochastic gradient descent. You might get confused about what these two terms do. Training a neural network means adjusting the weights of the model in such a way that the loss of the overall dataset is minimized.

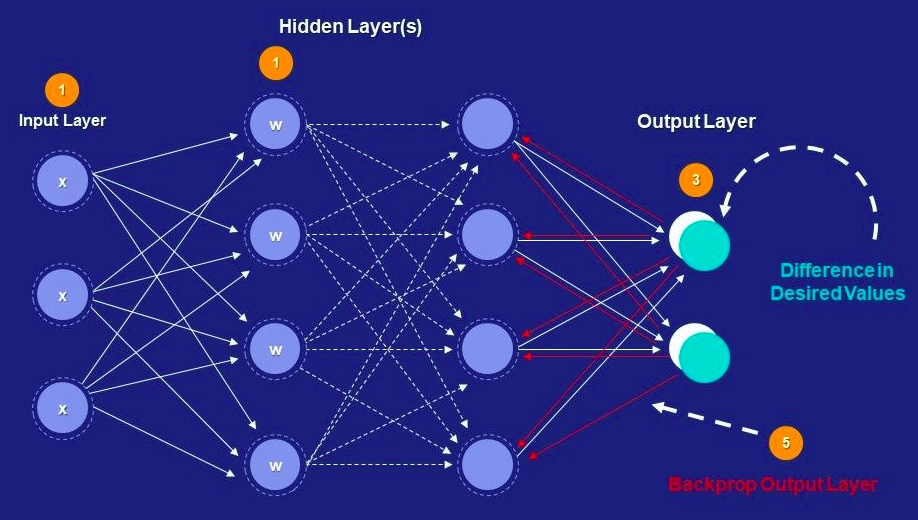
Forward propagation in training neural networks is just to calculate the loss of the model. While propagating backward, weights are updated to minimize the total loss. The forward and backward propagation is done until the loss is minimum. In this way, a neural network is trained. So, where do we need backpropagation and stochastic gradient descent?

In this article, we will see the use of backpropagation and stochastic gradient descent. Furthermore, we will discuss how backpropagation is different from stochastic gradient descent.

Backpropagation

To understand backpropagation, let us first see what gradient is. The gradient of the function gives an idea about the function, whether it is increasing or decreasing in a particular direction.

During the training of neural networks, the main goal is to minimize the cost function. We need to propagate backward and update the weights in order to minimize the cost. As the neural network may have many hidden layers and weights of every i^th layer depends on the i+1^th layer. Suppose the neural network has n layers. The weights of the n-1^th layer depend on the output layer, and the output is directly proportional to the cost function. Now, we will find the cost function derivative with respect to every weight and bias in the n-1^th layer. Using the chain rule, we can find the gradient of weight in any layer, i.e., dL/dw_i. We will obtain gradients for every weight; this result is used to update the weights by subtracting the result from the original weights. Hence the subtraction of the result from the weight(w_i - (lerning_rate)*dL/dw) may cause greater change. Therefore we use the learning rate to take baby steps to reach the minima of the cost function as shown below.

w_i = w_i - (lerning_rate)*dL/dw.

^source

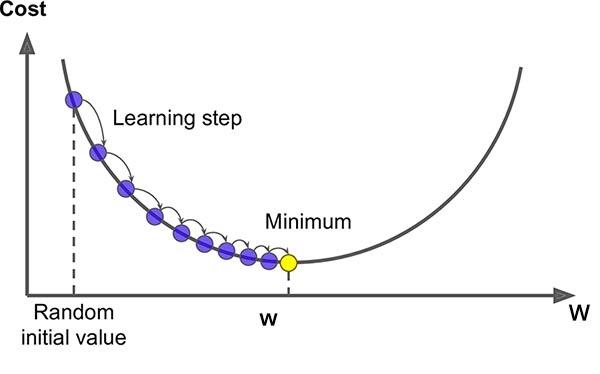
We will perform the above operation for every weight in every layer, so the overall value of the cost function is minimized.

In simple words, backpropagation is an algorithm where the information of cost function is passed on through the neural network in the backward direction.

Below is the image of backpropagation.

^source

Stochastic Gradient Descent

It is an optimization algorithm to update weights in the neural network that minimizes the cost of the neural network. The weights of neural networks in the stochastic gradient descent algorithms are updated using gradient calculated using the backpropagation algorithm.

Stochastic gradient descent is used at places having larger datasets. The normal gradient descent algorithm takes higher computation time as it calculates the cost for all the examples in the training dataset and performs backpropagation to update weights. In SGD, the cost is calculated for every training example in the dataset, and weights are updated.

Steps for Stochastic gradient descent

Shuffle the dataset.
Select the datapoint and cycle through all the data points in the dataset. (data points should not be repeatedly selected; this leads to the model overfitting).
Backpropagate the neural network.
Update the weights in each layer using the derivative of the cost function.
Subtract the current weight with the derivative of the cost function with respect to the current weight. (multiply the derivative with learning_rate to converge to global minima optimally)
Perform the above operation until cost function is optimized or global minima is achieved.

To know more about the stochastic gradient descent algorithm, visit the link.

Difference between backpropagation and stochastic gradient descent.

Backpropagation is an algorithm that efficiently calculates the gradient of the cost function with respect to the current weight in the neural network. Stochastic gradient descent is an optimizer that is used to update weights in the neural network. Both work simultaneously to minimize the cost function.

There is a misconception with people; they say that the model trained with backpropagation algorithm, but they forgot to specify the optimizer they have used. Instead, one should say “used backpropagation as gradient computing technique with SGD optimizer”.

FAQs

1. Why do we use backpropagation?

A: Backpropagation is an important mathematical algorithm used to calculate the gradient. It is used to improve prediction accuracy in Machine learning models and data mining. Generally, it is used by ANN to find the derivative of the cost function with respect to weights.

2. What is an SGD optimizer in keras?

A: Full form of SGD is stochastic gradient descent. It is an optimizer provided in keras with momentum and learning rate. The code below shows the implementation of the SGD optimizer.

from keras.optimizers import SGD
opt = SGD(lr=0.01, momentum=0.9)
model.compile(..., optimizer=opt)

3. What are optimizers?

A: Optimizers are algorithms or methods used to change the attributes of your neural network, such as weights and learning rate, to reduce the losses.