Introduction
Searching and Sorting are used to deal with data elements but both are different from each other. The key difference between the Searching and Sorting Algorithm is searching helps us search for a data element within a given string or array. On the other hand, Sorting is used for rearranging the data elements present in a string or an array in any specified order, whether ascending or descending.
This article will discuss searching and sorting, along with their different algorithms. We will also analyze the time and space complexity of the algorithms. This article will show the significant difference between Searching and Sorting on specific parameters.
What is Searching?
Searching is finding a particular item in a given list of items. It decides whether an element we are searching for is present or not. A search algorithm is an algorithm that accepts an argument "x"’ and tries to find an item in a given list whose value is equal to "x."
Searching for an element in a list can be done using Sequential search and Interval search.
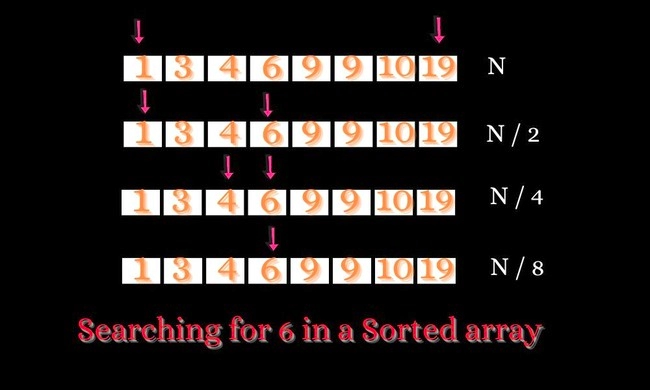
The image above shows searching for an element in a sorted array using binary search.
Code Implementation
#include <bits/stdc++.h>
using namespace std;
int Binary_Search(vector <int> &my_List, int element) {
int start = 0, end = my_List.size() - 1, index = -1;
while(start <= end) {
// find a mid
int mid = (start + end) / 2;
// check if our element is less than or equal to the element present at the mid index
if(my_List[mid] >= element) {
// now element present at mid can be our potential answer
index = mid;
// reduce the range because our element can't be at any index > mid
end = mid - 1;
}
else {
// reduce the range because our element can't be at any index < mid
start = mid + 1;
}
}
if(index != -1) {
if(my_List[index] != element) index = -1;
}
return index;
}
int main() {
vector <int> my_List = {1, 4, 15, 18, 22, 25};
int element = 18;
// search '18' in a given list and print its index
cout << Binary_Search(my_List, element);
return 0;
}Output:
3The code above uses a binary search algorithm to search a given element from the list.
Sequential Search
It is also known as Linear Search. It starts at the beginning of the list and compares every value on the list with the target value. If the target value matches the value in a list, then it returns the index of that element; otherwise, it returns -1.
Time Complexity
In the worst case (when the element we are searching for is present at the end of the list) we have to traverse the whole array. So, its Worst case time complexity will be O(n).
In the Best case, the element will be present at the beginning of the list. So we don’t need to traverse the array. Hence its Best case time complexity will be O(1).
Space Complexity
We don’t need any auxiliary space for this technique. So its space complexity will be O(1);
Interval Search
In this algorithm we only check certain parts of the dataset. Binary search is an example of an interval search algorithm. Binary Search works on sorted lists i.e., the list must be in increasing or decreasing order. It is based on a divide and conquer algorithm in which we compare our target value with the middle element of the list and based on that we reduce our search space by half. We continue this until we find our target element or our search space reduces to 1.
Time Complexity
The Worst case occurs when the algorithm keeps searching for the target until our search space reduces to 1. Since the number of comparisons are logn. So its Worst case time complexity will be O(logn).
The Best case occurs when the target is present in the middle. So only one comparison will be needed. Hence, its Best case time complexity will be O(1).
Space Complexity
We don’t need any auxiliary space for this technique. So its space complexity will be O(1);
Also Read - Selection Sort in C






