Breadth-first search is a graph searching algorithm. It finds the shortest path to all the other nodes from the given node in unweighted graphs.

What is the time complexity of BFS

?The time complexity of BFS is O(V + E), where V is the number of vertices and E is the number of edges.

Difference between the shortest and second shortest path in an Unweighted Bidirectional Graph

Problem Statement

You have an undirected unweighted graph having N vertices and M edges. You have to find the difference between the shortest and second shortest path. It is guaranteed that the given graph does not contain any self-loop and multiple edges.

Sample Test Cases

Input : 8 8        
    1 2
    2 3
    3 8
    1 4
    4 5
    5 6
    6 7 
    7 8
Output : 2
Explanation : N = 8, M = 8
          	  Shortest path : 1->2->3->8
          	  Second Shortest : 1->4->5->6->7->8 
          	  Difference : 2

Constraints

1 <= N <= 300000

1 <= M <= 300000

Approach

Brute force

The most straightforward approach is to find the length of all the paths recursively by using a depth-first search. We will store the lengths in a vector. Then we will sort that vector to get the shortest and second shortest path length.

Steps to solve

Define adjacency list G[][] to store the graph.
Define vector ‘lengths' to store the length of all the possible paths from 1 to N and vector 'vis' of size N + 1 to keep track of all the visited vertices.
Define a function 'DFS(int node, int &N, int cnt)' to find the length of all the possible paths.
- Base Case: if node == N, it means that we reached the Nth node starting from node 1 by traversing through one of the paths. So push cnt (length of the path) to vector lengths and terminate the recursive call.
- If node != N, then iterate over all the child 'u' of the vertex node, mark vis[u] = 1 and call DFS(u, N, cnt + 1).
- Set vis[u] to 0 to find all the other possible paths.
Call the DFS function by passing the parameters (1, N, 0).
sort the vector 'lengths' in non-decreasing order to find the length of the shortest and second shortest path.
If lengths.size() == 1, then there is only one path between 1 and N, so the final answer is 0 else lengths[1] - lengths[0] is the final answer.

Code

#include <bits/stdc++.h>
using namespace std;
const int M = 3e5 + 7;
//adjacency list G[][] to store the graph[][]
vector <vector<int>> G;
//vector to keep track of all the visited vertices
vector <int> vis;
//vector to store the length of all the possible paths from 1 to N
vector <int> lengths;

//function to find the length of all the possible paths.
void DFS(int node, int &N, int cnt){
   //Base Case
   if(node == N){
       lengths.push_back(cnt);
       return;
   }
   //iterate over all the child 'u' of the vertex node
   //mark vis[u] = 1 and call function to search all the paths
   //unmark vis[u]
   for(auto u : G[node]){
       if(vis[u] == 1)
           continue;
       vis[u] = 1;
       DFS(u, N, cnt + 1);
       vis[u] = 0;
   }
}
signed main(){
   int N, M;
   cin >> N >> M;
   G = vector <vector <int>> (N + 1);
   vis = vector <int> (N + 1, 0);
   for(int i = 0; i < M; ++i){
       int u, v;
       cin >> u >> v;
       G[u].push_back(v);
       G[v].push_back(u);
   }
   vis[1] = 1;
   //function call
   DFS(1, N, 0);
   //sort the vector 'lengths' in non-decreasing order 
   //to find the length of the shortest and second shortest path.
   sort(lengths.begin(), lengths.end());
   //If lengths.size() == 1, then there is only one path between 1 and N, so the final 
   if(lengths.size() < 2)
       cout << 0 << "\n";
   //else lengths[1] - lengths[0] is the final answer
   else
       cout << lengths[1] - lengths[0] << "\n";
   return 0;
}

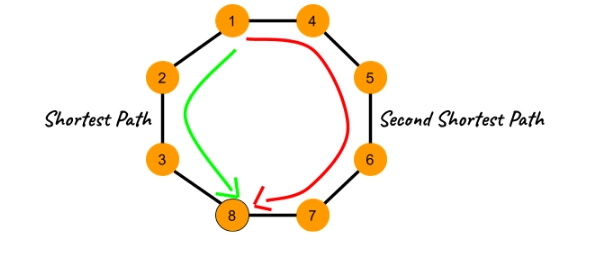
Input

Output

Time Complexity

The time complexity is O(2^N)

Space Complexity

The space complexity is O(N)

Efficient Approach

Observation: The second shortest path can't contain all the edges the same as the shortest path.

We can find all the edges in the shortest path by using breadth-first search. Then we will keep finding the length of the shortest path by removing each edge one by one. The minimum of them is the length of the second shortest path.

Steps to find all the edges in the shortest path

Define a function 'find_edges(int &N)' that will return a vector of pairs containing all the edges in the shortest path of the given graph.
Define vector 'dis' to store the length of the shortest path to each node and vector 'par' to store the parent of each node.
Initialize 'dis' by INT_MAX and 'par' by 0.
Start the BFS traversal from node 1.
While doing the BFS, store the shortest distance to each node and also maintain the parent vector.
Recover the path by using the parent vector.
Define a vector of pair ‘edges’.
While recovering, the path if we are at vertex node and par[node] != 0 then push {node, par[node]} to vector edges and if par[node] == 0 then terminate the loop.

Steps to solve

Define adjacency list G[][] to store the graph and a vector 'lengths' to store the length of possible paths.
Declare a vector 'edges' to store the edges of the shortest path.
Find all the edges in the shortest path of the given graph using the steps mentioned above and store them in the vector edges. While finding it, push dis[N] (shortest path length) in the vector lengths.
Define a function 'find_shortest_path(int &N, pair <int, int> &skip)' to find the length of shortest path by removing edge 'skip'.
- Define vector 'dis' to store the shortest path length to each node.
- Initialize 'dis' by INT_MAX.
- Start the BFS traversal from node 1.
- While doing the BFS, if u is one of the neighbors of the vertex node, then there is an edge between the vertex node and vertex u. The edge can be 'X' = {node, u} or 'Y' = {u, node}.
- If X == skip or Y == skip, ignore the edge between vertex node and u.
- push dis[N] (shortest path length) in the vector lengths.
Iterate over all the elements u in vector edges and call the function find_shortest_path(N, u).
Sort the vector 'lengths' in non-decreasing order to find the length of the shortest and second shortest path.
If lengths.size() == 1, then there is only one path between 1 and N, so the final answer is 0 else lengths[1] - lengths[0] is the final answer.

Code

#include <bits/stdc++.h>
using namespace std;
const int M = 3e5 + 7;
//adjacency list G[][] to store the graph
vector <vector<int>> G;
//vector 'lengths' to store the length of possible paths
vector <int> lengths;
//function that will return a vector of pairs containing all 
//the edges in the shortest path of the given graph
vector <pair<int, int>> find_edges(int &N){
   //vector to store the length of the shortest path to each node
   vector <int> dis(N + 1, INT_MAX);
   //vector to store the parent of each node
   vector <int> par(N + 1);
   //queue for BFS traversal
   queue <int> q;
   //distance from node 1 to iteself is 0
   dis[1] = 0;
   //start the BFS traversal from node 1
   q.push(1);
   while(!q.empty()){
       int node = q.front();
       q.pop();
       for(auto u : G[node]){
           if(dis[u] == INT_MAX){
               //storing parent
               par[u] = node;
               dis[u] = dis[node] + 1;
               q.push(u);
           }
       }
   }
   vector <pair<int, int>> edges; //vector to store all the edges in shortest path
   int node = N;
   //recover the path by using the parent vector
   while(par[node]){
       edges.push_back({node, par[node]});
       node = par[node];
   }
   //push length of the shortest path 
   lengths.push_back(dis[N]);
   return edges;
}
void find_shortest_path(int &N, pair <int, int> &skip){
   
   //vector 'dis' to store the shortest path length to each node
   vector <int> dis(N + 1, INT_MAX);  
   //for BFS
   queue <int> q;
   //Start the BFS traversal from node 1
   dis[1] = 0;
   q.push(1);
   while(!q.empty()){
       int node = q.front();
       q.pop();
       for(auto u : G[node]){
           //the edge between vertex node and vertex u can be 'X' = {node, u} or 'Y' = {u, node}
           pair <int, int> X = {u, node}, Y = {node, u};
           //If X == skip or Y == skip,  ignore the edge between vertex node and u
           if(X == skip || Y == skip)
               continue;
           if(dis[u] == INT_MAX){
               dis[u] = dis[node] + 1;
               q.push(u);
           }
       }
   }
   //push dis[N] (shortest path length) in the vector lengths
   lengths.push_back(dis[N]);
}
signed main(){
   int N, M;
   cin >> N >> M;
   G = vector <vector <int>> (N + 1);
   for(int i = 0; i < M; ++i){
       int u, v;
       cin >> u >> v;
       G[u].push_back(v);
       G[v].push_back(u);
   }
   //finding all the edges in shortest path
   vector <pair<int, int>> edges = find_edges(N);
   //iterate over all the elements u in vector edges and call the function find_shortest_path(N, u)
   for(auto skip : edges){
       find_shortest_path(N, skip);
   }
   //sort the vector 'lengths' in non-decreasing order 
   //to find the length of the shortest and second shortest path.
   sort(lengths.begin(), lengths.end());
   //If lengths.size() == 1, then there is only one path between 1 and N, so the final 
   if(lengths.size() < 2)
       cout << 0 << "\n";
   //else lengths[1] - lengths[0] is the final answer
   else
       cout << lengths[1] - lengths[0] << "\n";

   return 0;
}

Time Complexity

The time complexity is O(N * M)

Space Complexity

The space complexity is O(N)

FAQs

What is BFS?
Breadth-first search is a graph searching algorithm. It finds the shortest path to all the other nodes from the given node in unweighted graphs.
What is the time complexity of BFS?
The time complexity of BFS is O(V + E), where V is the number of vertices and E is the number of edges.

Key Takeaways

In this article, we solved a graph theory problem. Having a good grasp of graph theory is very important for cracking coding interviews at MAANG.

Check out this coding ninjas' blog on graph theory algorithms for getting a better hold on it.

Check out this problem - Root To Leaf Path

To learn more about such data structures and algorithms, Coding Ninjas Studio is a one-stop destination. This platform will help you to improve your coding techniques and give you an overview of interview experiences in various product-based companies by providing Online Mock Test Series and many more benefits.

Happy learning!