Introduction 🥳
In this article, the primary distinctions between Floyd–Warshall’s Algorithm and Dijkstra’s Algorithm for the shortest path will be covered. For a deeper understanding, we will compare them further based on several aspects.

Both techniques work with the graph Data Structure. A graph is made up of a collection of nodes, also known as vertices, denoted by the letter V, and a set of connections, also known as edges, denoted by the letter E. In addition, we give each edge a non-negative integer weight that corresponds to the distance metric between any two nodes. The distance separating two nodes is equal to the weights of the edges that make up the path. Finding the path with the shortest distance between node pairs is therefore crucial.
Dijkstra’s Algorithm
Dijkstra’s Algorithm is used to resolve the Single Source Shortest Path issue. In other words, we want to identify the shortest route between a particular source node and a specific destination node. This algorithm is used effectively in the link-state routing protocol, where each node applies it to build an internal representation of the network.
Step 1: Create a weighted graph first, where each branch is given a certain numerical weight. Similarly, a weighted graph is a specific type of labeled graph where the labels are numerical values (which are positive).
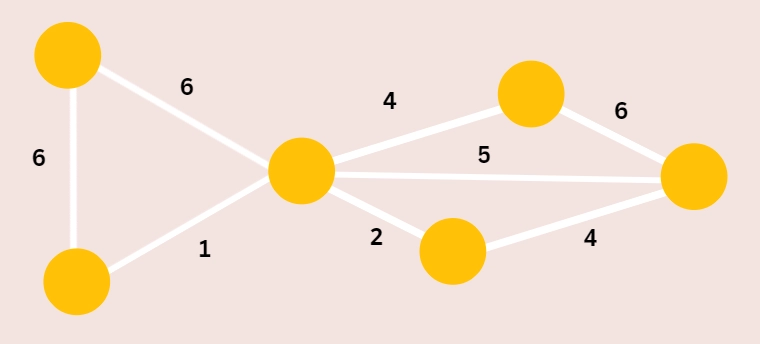
Step 2: Choose a starting vertex, and give all other components route values of infinite.
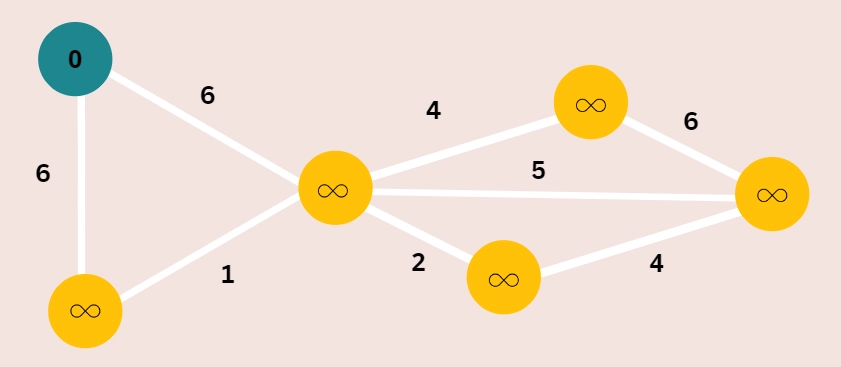
Step 3: Update each vertex's path length stopping by.
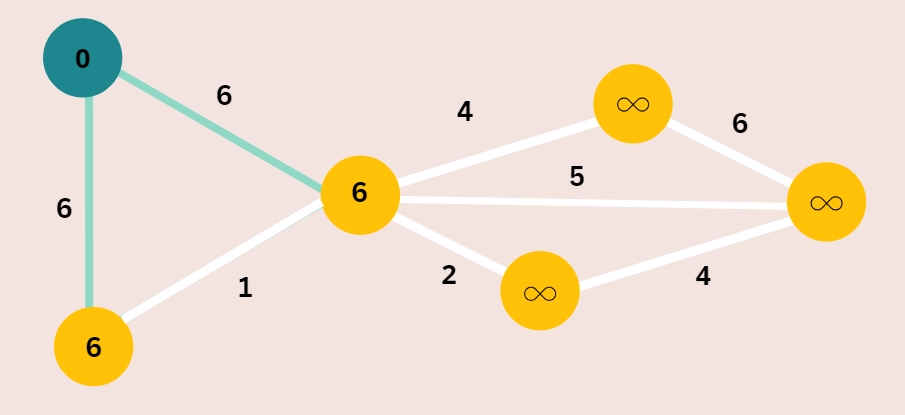
Step 4: Do not update a vertex if its path length is less than the new path length.
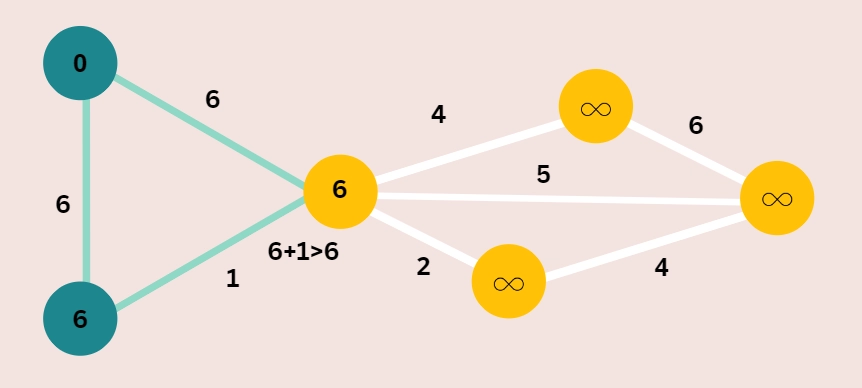
Step 5: Don't alter the path lengths of vertices that have already been visited.
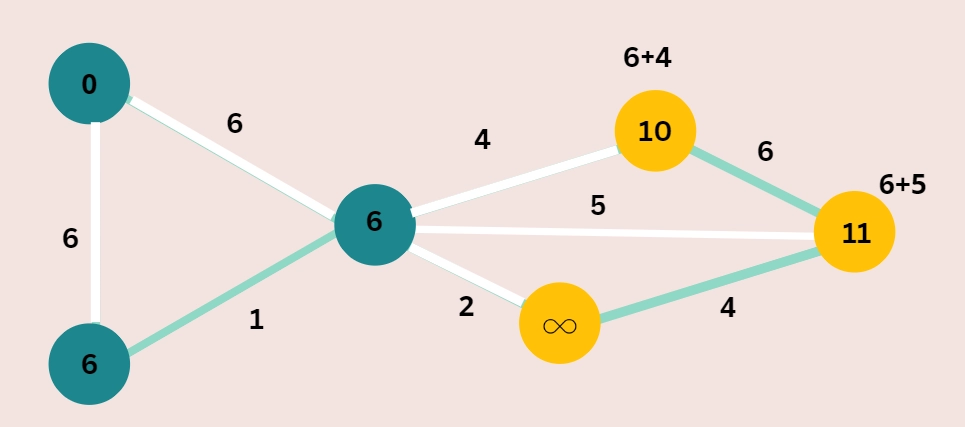
Dijkstra’s Algorithm adheres to the concept of greed. As a result, it terminates with a globally optimal solution by making locally optimal decisions at each stage. The optimal substructure and greedy choice property are the distinguishing features of a problem that a greedy algorithm can solve. These algorithms run in a top-down manner.
By "optimal substructure," we imply that a problem's optimal solution is made up of the best possible answers to each of its subproblems. For instance, the Unweighted Longest Simple Path issue lacks optimum substructure while the SSSP problem does.
Refer to the blog “Dijkstra's Algorithm” for a detailed analysis and code implementation of it.