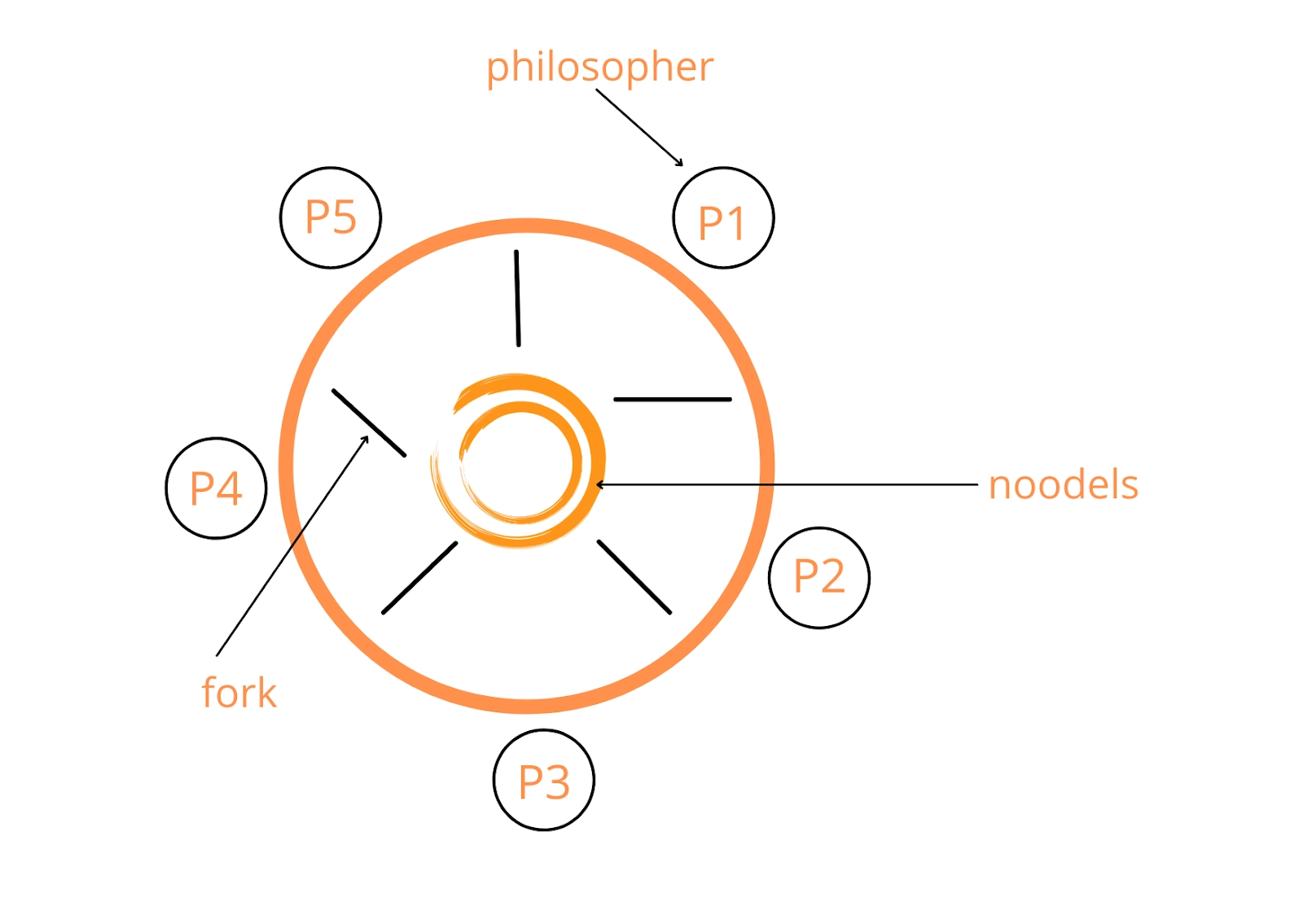
Dining Philosopher Solution Using Monitors

Dining-Philosophers Solution Using Monitor

We demonstrate monitor ideas by proposing a deadlock-free solution to the Dining-Philosophers problem. The monitor is used to control access to state variables and condition variables. It only notifies when to enter and exit the segment.

This approach imposes the limitation that a philosopher may only take up her forks if both the forks are available.

To code this solution, we must distinguish between three situations where we could see a philosopher. We introduce the following data structure for this purpose:

Thinking: When the philosopher does not want to use either fork.

Hungry: When a philosopher wishes to use the forks, i.e., he wants to go to the critical section.

Eating: When the philosopher has both forks, i.e., he has entered the critical section.

Philosopher i may set the variable state[i] = Eating, Only if her two neighbours are not eating,i.e., (state[(i+4)%5]!= Eating) and (state[(i+1)%5]!= Eating).

Solution Code

// Dining-Philosophers Solution Using Monitors
monitor DiningPhilosophers
{
    status state[5];
    condition self[5];

    // Picking up forks
    void Pick(int i)
    {
        // indicating HUNGRY state
        state[i] = HUNGRY;

        // setting state to EATING in test()
        // only if the left and right neighbors if current        //philosopher are not EATING
        test(i);

        // if unable to eat,then waiting to be signaled
        if (state[i] != EATING)
            self[i].wait;
    }

   // Putting down the forks
    void Put(int i)
    {

        // indicating THINKING state
        state[i] = THINKING;

        // if right neighbor R=(i+1)%5 is HUNGRY and
        // both of R's neighbors are not EATING,
        // then setting the R's state to EATING and waking it up               // by signaling R's CV
        test((i + 1) % 5);
        test((i + 4) % 5);
    }

    void test(int i)
    {

        if (state[(i + 1) % 5] != EATING && state[(i + 4) % 5] != EATING && state[i] == HUNGRY)
        {

            // indicating EATING state
            state[i] = EATING;

            // signal() has no effect during Pick(),but is //important to wake up waiting HUNGRY philosophers during Put()
            self[i].signal();
        }
    }

    initialization_code()
    {

        // Execution of Pick(), Put() and test() are all mutually //exclusive, i.e. only one at a time can be executed
        for (int i = 0; i < 5; i++)
            state[i] = THINKING;
        // Verifying that this monitor-based solution is deadlock //free and mutually exclusive in that no 2 neighbors can eat //simultaneously
   }
} // end of monitor

We must also declare :

condition self[5];

This enables Philosopher i to postpone her meal when she is hungry but unable to procure the forks she requires.

We may now discuss our solution to the Dining-Philosophers problem. The monitor Dining Philosophers controls the fork distribution.

Before beginning to eat, each philosopher must invoke the operation pick(). The philosopher's process may be halted as a result of this conduct.

The philosopher may eat when the procedure is completed successfully.

Following that, the philosopher calls the put() function.

As a result, philosopher i must invoke the actions pick() and put() in the following order:

DiningPhilosophers.pick(i);

              ...

              eat

              ...

DiningPhilosophers.put(i);

We can now easily see that this solution ensures that no two neighbors are eating simultaneously and that no deadlocks will occur. However, we should point out that it is possible for a philosopher to starve to death.

Also see, Open Source Operating System

Frequently Asked Questions

What are monitors in OS?

Monitors are programming language constructs that help in regulating shared data access.
The Monitor is a module or package that contains a common data structure, procedures, and the synchronization of concurrent procedure invocations.

What is the advantage of using the monitor in the operating system?

• Monitors are less challenging to build than semaphores.
• Mutual exclusion in monitors is automatic. However, mutual exclusion in semaphores must be manually established.
• Monitors can compensate for the timing faults that arise when semaphores are used.

What happens if all the philosophers pick the left fork first and then the right fork in the DP problem?

If philosopher P is unable to eat at this time, it is because he either does not have any forks or has his right fork.
Philosopher P can eat once his left fork is accessible if he possesses his right fork.

How many philosophers may eat simultaneously in the dining philosophers problem with five philosophers if they all picked up a fork simultaneously?

If all philosophers are hungry at the same moment, only two philosophers may eat because philosophers used two forks simultaneously.

Conclusion

In this article. we discussed the Dining Philosophers problem and its solution using Monitors. We also touched briefly on some of the important operating system concepts. 

Recommended Reading

• Introduction to Operating System
• Producer-Consumer Problem using Semaphores
• Reader-Writer's Problem
• Sleeping Barber Problem
• Deadlock Detection Algorithm
• Deadlock v/s Starvation
• Top Operating Systems Interview Questions
• Open Source Operating System
• FCFS Scheduling

On the other hand, learning never ceases, and there is always more to learn. So, keep learning and keep growing, ninjas!

Check out some of our Courses as well as Guided Paths on Coding Ninjas Studio

Good luck with your preparation!