Introduction
The LU decomposition is the factorization of a square matrix into two triangular matrices, one upper triangular matrix, and one lower triangular matrix, with the product of these two matrices equaling the original matrix.
LU decomposition has a variety of applications, including solving a system of equations, which is an integral part of many other applications, such as finding current in a circuit, finding the inverse of a matrix, and finding the determinant of a matrix.
Doolittle’s Algorithm provides a way to factor a matrix A into an LU decomposition.
Doolittle Algorithm
A square matrix can always be factored into a lower triangular matrix and an upper triangular matrix. In other words, [A] = [L][U].
Doolittle's method allows us to factor A into a LU decomposition without going through the complexity of Gaussian Elimination.
We assume that a LU decomposition exists for a general n×n matrix A and write the form of L and U directly. We then systematically use the equations from the multiplications required for A = LU to solve the entries in L and U.
A = LU can be expanded as follow:
![<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="[" close="]"><mtable><mtr><mtd><msub><mi>A</mi><mn>00</mn></msub></mtd><mtd><msub><mi>A</mi><mn>01</mn></msub></mtd><mtd><msub><mi>A</mi><mn>02</mn></msub></mtd></mtr><mtr><mtd><msub><mi>A</mi><mn>10</mn></msub></mtd><mtd><msub><mi>A</mi><mn>11</mn></msub></mtd><mtd><msub><mi>A</mi><mn>12</mn></msub></mtd></mtr><mtr><mtd><msub><mi>A</mi><mn>20</mn></msub></mtd><mtd><msub><mi>A</mi><mn>21</mn></msub></mtd><mtd><msub><mi>A</mi><mn>22</mn></msub></mtd></mtr></mtable></mfenced><mo> </mo><mo>=</mo><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><msub><mi>L</mi><mn>10</mn></msub></mtd><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><msub><mi>L</mi><mn>20</mn></msub></mtd><mtd><msub><mi>L</mi><mn>21</mn></msub></mtd><mtd><mn>1</mn></mtd></mtr></mtable></mfenced><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><msub><mi>U</mi><mn>00</mn></msub></mtd><mtd><msub><mi>U</mi><mn>01</mn></msub></mtd><mtd><msub><mi>U</mi><mn>02</mn></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><msub><mi>U</mi><mn>11</mn></msub></mtd><mtd><msub><mi>U</mi><mn>12</mn></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd><mtd><msub><mi>U</mi><mn>22</mn></msub></mtd></mtr></mtable></mfenced><mo> </mo><mspace linebreak="newline"/></math>](https://files.codingninjas.in/article_images/doolittle-algorithm-0-1646477543.webp)
The terms of the U matrix is given by:
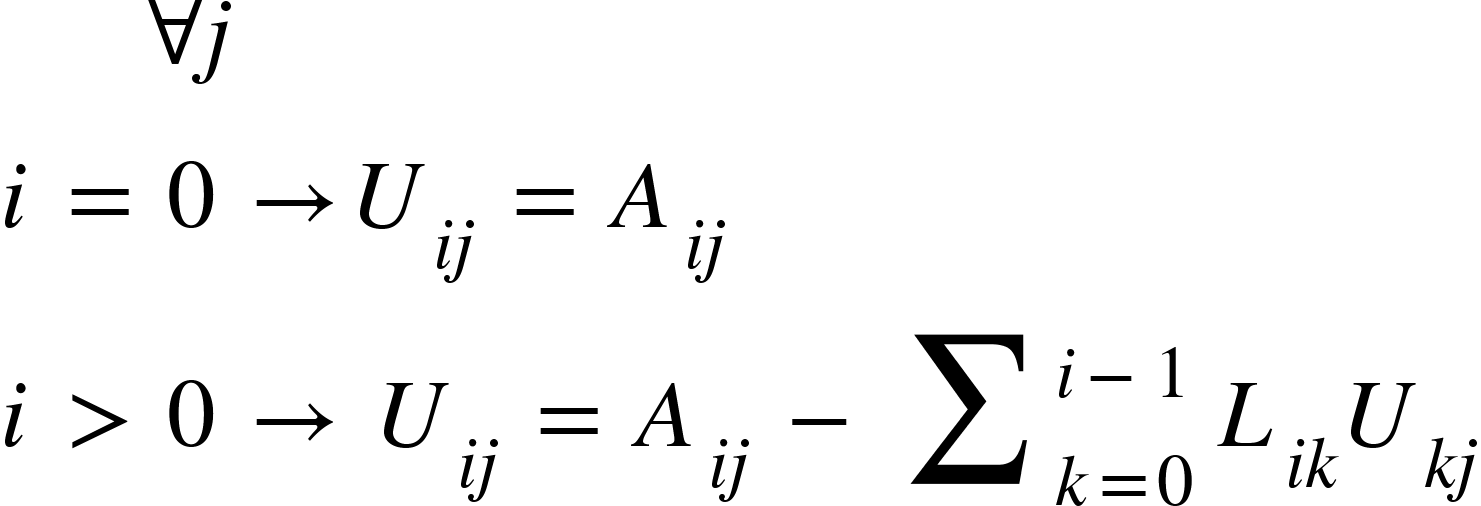
The terms of the L matrix is given by:
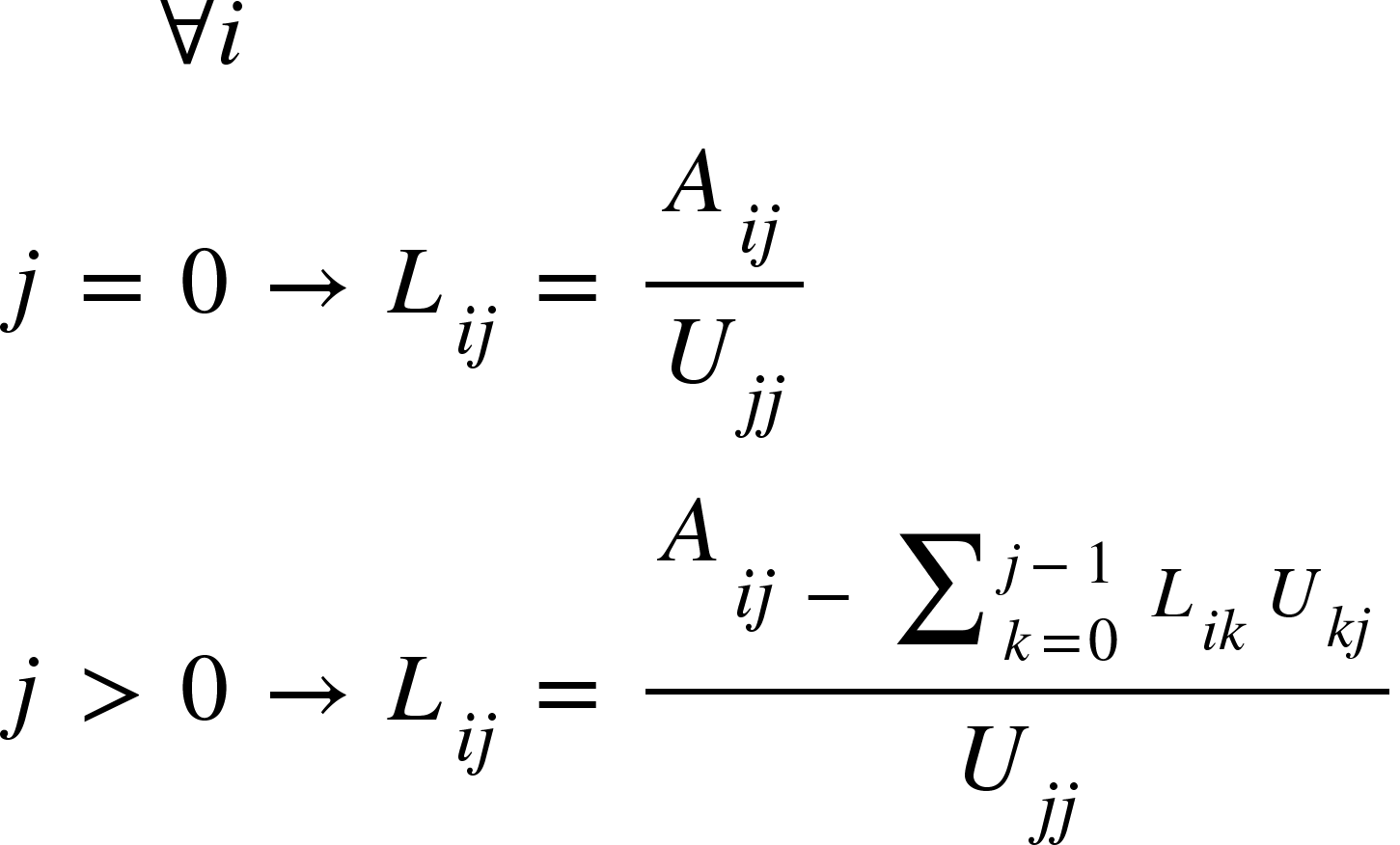
Example
Given a matrix A, decompose it to Lower and Upper triangular matrix using the Doolittle algorithm.
![<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo> </mo><mo>=</mo><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>2</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>3</mn></mtd></mtr></mtable></mfenced><mo> </mo></math>](https://files.codingninjas.in/article_images/doolittle-algorithm-3-1646477544.webp)
Solution:
Using Doolittle’s algorithm, we can write A = LU, where L is the lower triangular matrix and U is the upper triangular matrix.
![<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>2</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>3</mn></mtd></mtr></mtable></mfenced><mo> </mo><mo>=</mo><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><msub><mi>l</mi><mn>10</mn></msub></mtd><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><msub><mi>l</mi><mn>20</mn></msub></mtd><mtd><msub><mi>l</mi><mn>21</mn></msub></mtd><mtd><mn>1</mn></mtd></mtr></mtable></mfenced><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><msub><mi>u</mi><mn>00</mn></msub></mtd><mtd><msub><mi>u</mi><mn>01</mn></msub></mtd><mtd><msub><mi>u</mi><mn>02</mn></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><msub><mi>u</mi><mn>11</mn></msub></mtd><mtd><msub><mi>u</mi><mn>12</mn></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd><mtd><msub><mi>u</mi><mn>22</mn></msub></mtd></mtr></mtable></mfenced><mspace linebreak="newline"/></math>](https://files.codingninjas.in/article_images/doolittle-algorithm-4-1646477545.webp)
Now, multiply the L and U matrix.
![<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><msub><mi>l</mi><mn>10</mn></msub></mtd><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><msub><mi>l</mi><mn>20</mn></msub></mtd><mtd><msub><mi>l</mi><mn>21</mn></msub></mtd><mtd><mn>1</mn></mtd></mtr></mtable></mfenced><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><msub><mi>u</mi><mn>00</mn></msub></mtd><mtd><msub><mi>u</mi><mn>01</mn></msub></mtd><mtd><msub><mi>u</mi><mn>02</mn></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><msub><mi>u</mi><mn>11</mn></msub></mtd><mtd><msub><mi>u</mi><mn>12</mn></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd><mtd><msub><mi>u</mi><mn>22</mn></msub></mtd></mtr></mtable></mfenced><mo> </mo><mo>=</mo><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><msub><mi>u</mi><mn>00</mn></msub></mtd><mtd><msub><mi>u</mi><mn>01</mn></msub></mtd><mtd><msub><mi>u</mi><mn>02</mn></msub></mtd></mtr><mtr><mtd><msub><mi>l</mi><mn>10</mn></msub><mo>·</mo><msub><mi>u</mi><mrow><mn>00</mn><mo> </mo></mrow></msub></mtd><mtd><msub><mi>l</mi><mn>10</mn></msub><mo>·</mo><msub><mi>u</mi><mn>01</mn></msub><mo>+</mo><msub><mi>u</mi><mn>11</mn></msub></mtd><mtd><mo> </mo><msub><mi>l</mi><mn>10</mn></msub><mo>·</mo><msub><mi>u</mi><mn>02</mn></msub><mo>+</mo><msub><mi>u</mi><mn>12</mn></msub></mtd></mtr><mtr><mtd><msub><mi>l</mi><mn>20</mn></msub><mo>·</mo><msub><mi>u</mi><mn>00</mn></msub></mtd><mtd><mo> </mo><mo> </mo><msub><mi>l</mi><mn>20</mn></msub><mo>·</mo><msub><mi>u</mi><mn>01</mn></msub><mo>+</mo><msub><mi>l</mi><mn>21</mn></msub><mo>·</mo><msub><mi>u</mi><mn>11</mn></msub><mo> </mo></mtd><mtd><mo> </mo><msub><mi>l</mi><mn>20</mn></msub><mo>·</mo><msub><mi>u</mi><mn>02</mn></msub><mo>+</mo><msub><mi>l</mi><mn>21</mn></msub><mo>·</mo><msub><mi>u</mi><mn>12</mn></msub><mo>+</mo><msub><mi>u</mi><mn>22</mn></msub></mtd></mtr></mtable></mfenced><mspace linebreak="newline"/></math>](https://files.codingninjas.in/article_images/doolittle-algorithm-5-1646477545.webp)
Now, compare the multiplied LU matrix with the A matrix row by row.
![<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>2</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>3</mn></mtd></mtr></mtable></mfenced><mo> </mo><mo>=</mo><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><msub><mi>u</mi><mn>00</mn></msub></mtd><mtd><msub><mi>u</mi><mn>01</mn></msub></mtd><mtd><msub><mi>u</mi><mn>02</mn></msub></mtd></mtr><mtr><mtd><msub><mi>l</mi><mn>10</mn></msub><mo>·</mo><msub><mi>u</mi><mn>00</mn></msub></mtd><mtd><msub><mi>l</mi><mn>10</mn></msub><mo>·</mo><msub><mi>u</mi><mn>01</mn></msub><mo>+</mo><msub><mi>u</mi><mn>11</mn></msub></mtd><mtd><msub><mi>l</mi><mn>10</mn></msub><mo>·</mo><msub><mi>u</mi><mn>02</mn></msub><mo>+</mo><msub><mi>u</mi><mn>12</mn></msub></mtd></mtr><mtr><mtd><msub><mi>l</mi><mn>20</mn></msub><mo>·</mo><msub><mi>u</mi><mn>00</mn></msub></mtd><mtd><mo> </mo><mo> </mo><msub><mi>l</mi><mn>20</mn></msub><mo>·</mo><msub><mi>u</mi><mn>01</mn></msub><mo>+</mo><msub><mi>l</mi><mn>21</mn></msub><mo>·</mo><msub><mi>u</mi><mn>11</mn></msub><mo> </mo></mtd><mtd><msub><mi>l</mi><mn>20</mn></msub><mo>·</mo><msub><mi>u</mi><mn>02</mn></msub><mo>+</mo><msub><mi>l</mi><mn>21</mn></msub><mo>·</mo><msub><mi>u</mi><mn>12</mn></msub><mo>+</mo><msub><mi>u</mi><mn>22</mn></msub></mtd></mtr></mtable></mfenced><mspace linebreak="newline"/></math>](https://files.codingninjas.in/article_images/doolittle-algorithm-6-1646477545.webp)
After comparing each row element in both the above matrices, we will get the values of unknowns as follows:
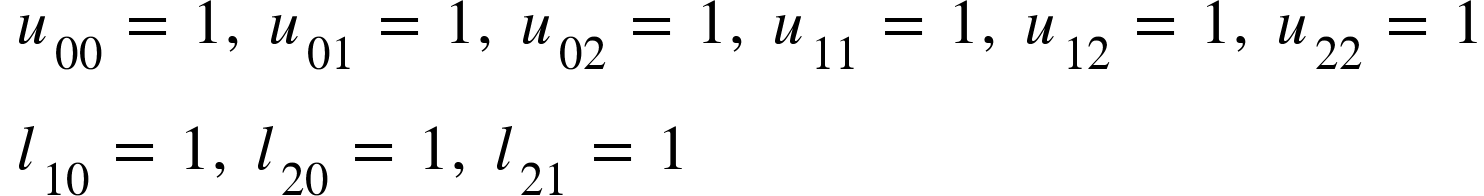
So finally, the L and U matrix becomes:
![<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>L</mi><mo> </mo><mo>=</mo><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd></mtr></mtable></mfenced><mspace linebreak="newline"/><mspace linebreak="newline"/><mi>U</mi><mo> </mo><mo>=</mo><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>1</mn></mtd></mtr></mtable></mfenced></math>](https://files.codingninjas.in/article_images/doolittle-algorithm-8-1646477546.webp)
Code Example
The C++ program to calculate the Upper and Lower Triangular Matrix is given below:
#include <bits/stdc++.h>
using namespace std;
const int MAX = 100;
void LUDecomposition(int mat[][MAX], int n)
{
int lower[n][n], upper[n][n];
memset(lower, 0, sizeof(lower));
memset(upper, 0, sizeof(upper));
// Decomposing matrix into Upper and Lower triangular matrix
for (int i = 0; i < n; i++)
{
// Upper Triangular
for (int k = i; k < n; k++)
{
// Summation of L(i, j) * U(j, k)
int sum = 0;
for (int j = 0; j < i; j++)
sum += (lower[i][j] * upper[j][k]);
// Evaluating U(i, k)
upper[i][k] = mat[i][k] - sum;
}
// Lower Triangular
for (int k = i; k < n; k++)
{
if (i == k)
lower[i][i] = 1; // Diagonal as 1
else
{
// Summation of L(k, j) * U(j, i)
int sum = 0;
for (int j = 0; j < i; j++)
sum += (lower[k][j] * upper[j][i]);
// Evaluating L(k, i)
lower[k][i] = (mat[k][i] - sum) / upper[i][i];
}
}
}
// setw is for displaying in correct manner
cout << setw(6)
<< " Lower Triangular"
<< setw(32)
<< " Upper Triangular" << endl;
// Printing the result
for (int i = 0; i < n; i++)
{
// Lower Triangular Matrix
for (int j = 0; j < n; j++)
cout << setw(6) << lower[i][j] << "\t";
cout << "\t";
// Upper Triangular Matrix
for (int j = 0; j < n; j++)
cout << setw(6) << upper[i][j] << "\t";
cout << endl;
}
}
int main()
{
int mat[][MAX] = {{1, 1, 1}, {1, 2, 2}, {1, 2, 3}};
LUDecomposition(mat, 3);
return 0;
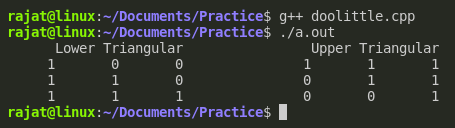
}Output:
The matrix we decomposed is:
![<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo> </mo><mo>=</mo><mo> </mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>2</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>3</mn></mtd></mtr></mtable></mfenced><mo> </mo></math>](https://files.codingninjas.in/article_images/doolittle-algorithm-3-1646477544.webp)