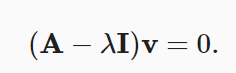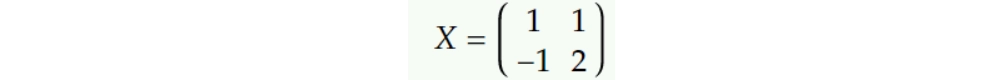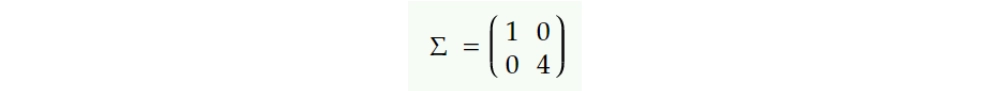Eigenvalue Decomposition

How Eigendecomposition Works

Eigendecomposition involves finding the eigenvectors and eigenvalues of a given matrix. The eigenvectors represent the directions of the transformation, while the eigenvalues represent the scaling factor along those directions.

How to Use Eigendecomposition to Find the Eigenvalues

To find the eigenvalues of a matrix 𝐴A, we solve the characteristic equation det⁡(𝐴−𝜆𝐼)=0, where 𝜆 represents the eigenvalues and I is the identity matrix.

How to Use Eigendecomposition to Find the Eigenvectors

Once the eigenvalues are obtained, we substitute each eigenvalue into the equation (𝐴−𝜆_𝑖𝐼)𝑣_𝑖=0 and solve for the corresponding eigenvector 𝑣_𝑖.

Eigendecomposition and Matrix Reconstruction Example

Suppose we have a matrix 𝐴A representing a linear transformation. By performing eigendecomposition, we find eigenvectors 𝑣₁,𝑣₂,…,𝑣_𝑛 and eigenvalues 𝜆₁,𝜆₂,…,𝜆_𝑛​. We can then reconstruct the original matrix 𝐴A using the formula 𝐴=𝑃𝐷𝑃⁻¹, where 𝑃 is a matrix composed of the eigenvectors as columns, and 𝐷 is a diagonal matrix containing the eigenvalues. This allows us to understand and manipulate the transformation represented by 𝐴 more intuitively.

How to Find Eigenvalues

Let's see how we can find them. By removing the λv from both sides and then factoring out the vector, We can see that the above is identical to:                      

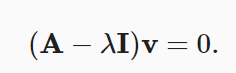
Because the preceding equation must compress some direction to zero, it is not invertible. Thus, the determinant is zero.

Thus, we can evaluate the eigenvalues by finding for what  λ  is :

det(A−λI)=0

Once we get the eigenvalues, we can compute Av=λv  to find the relevant eigenvector(s).

The built-in numpy.linalg.eig method can be used to check this in code.
 

%matplotlib inline
import numpy as np
from IPython import display
from d2l import mxnet as d2l

 
np.linalg.eig(np.array([[4, 2], [4, 6]]))

You can also try this code with Online Python Compiler

Run Code

Decomposition

Let X be a matrix with columns equal to the eigenvectors of matrix A,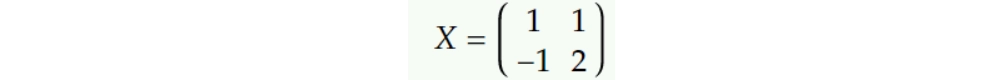                                                                                                                    

Let Σ be the diagonal matrix with the associated eigenvalues,

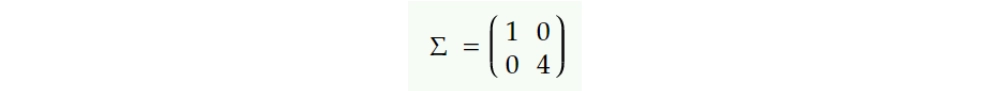
The definition of eigenvalues and eigenvectors, on the other hand, tells us that

AX=XΣ

As the matrix X is invertible,

 A=XΣX^-1

Calculation of Eigendecomposition

Using the eig() function in NumPy, you may calculate the eigendecomposition,

# eigendecomposition
from numpy import array
from numpy.linalg import eig
# define matrix
A = array([[1, 2, 3], [4, 10, 16], [17, 18, 19]])
print(A)
# calculate eigendecomposition
values, vectors = eig(A)
print(values)
print(vectors)

You can also try this code with Online Python Compiler

Run Code

Frequently Asked Questions

What happens if the eigenvalues are nearly equal?

PCA will not choose the principal components if all eigenvectors are the same because all principal components will be similar.

What are the applications of eigenvalue decomposition?

Eigenvalue decomposition finds applications in principal component analysis (PCA), solving differential equations, data compression, image processing, and spectral analysis. It's used in machine learning for feature extraction, dimensionality reduction, and clustering algorithms like k-means.

Is eigenvalue decomposition same as SVD?

Eigenvalue decomposition and singular value decomposition (SVD) are related but not identical. Both methods decompose matrices, but SVD is more general and applicable to non-square and singular matrices, while eigenvalue decomposition is limited to square matrices.

Is SVD faster than eigendecomposition?

In general, SVD is computationally more expensive than eigenvalue decomposition. However, SVD is more numerically stable and applicable to a wider range of matrices, making it preferred for many applications, including data analysis and signal processing.

Conclusion

In this post, we learned how eigendecomposition works and how to compute and interpret eigenvalues and eigenvectors. We finished with a final example in which we disassembled and reassembled a matrix using only NumPy's built-in functions.

The principal component analysis relies heavily on eigendecomposition. The computation of the eigenvalues, on the other hand, is not as straightforward as it appears in our examples. As a result, numerous iterative techniques are available to address this problem.