Introduction
A combinational circuit is a circuit in which we combine the different gates in the circuit. For example: decoder, encoder, multiplexer, and Demultiplexer.
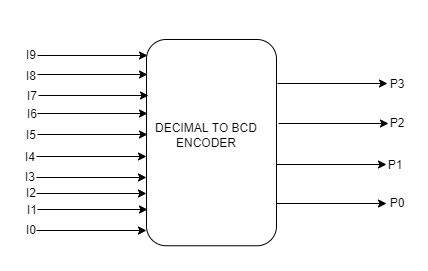
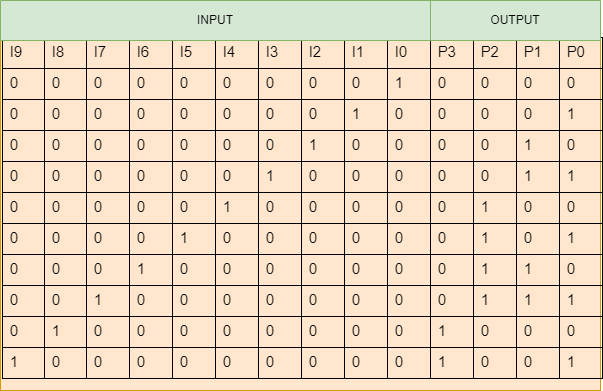
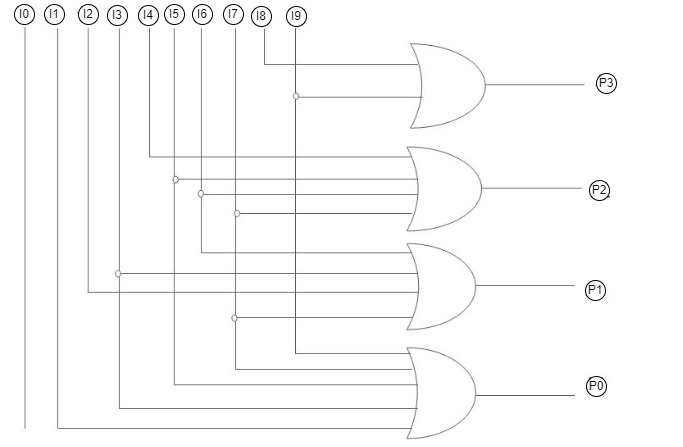
In this article, we will discuss an overview of an encoder which is a combinational circuit that converts binary information in the form of 2^n input lines into n output lines, which represent N bit code for the input.
Read About - Shift Registers in Digital Electronics and Difference Between Jfet and Mosfet
Encoders
These are combinational circuits that perform the opposite operation of Decoders. It can support up to 2^n input lines and 'n' output lines. It will generate a binary code equal to the input, which is active High. As a result, the encoder encodes 2^n input lines using 'n' bits. Encoders may or may not represent the enable signal.
An encoder is either a device, a transducer, or a circuit. The encoder will convert data from one format to another, such as electrical signals to counters or PLCs. The encoder's feedback signal will determine the position, count, speed, and direction. Control devices are used to route commands to specific functions.
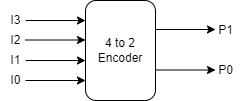
4:2 Encoder
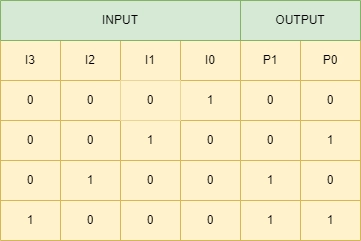
The 4:2 Encoder has four inputs (I3, I2, I1, and I0) and two outputs (P1 and P0). Only one of these four inputs can be '1' at a time to get the corresponding binary code at the output.
The truth table for the 4:2 encoder is as follows:
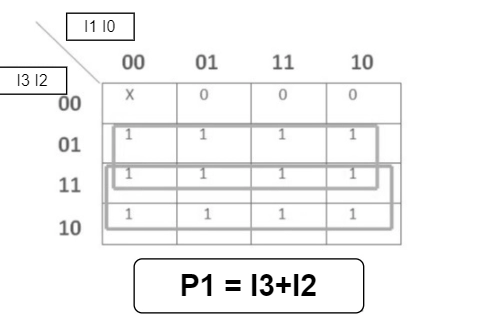
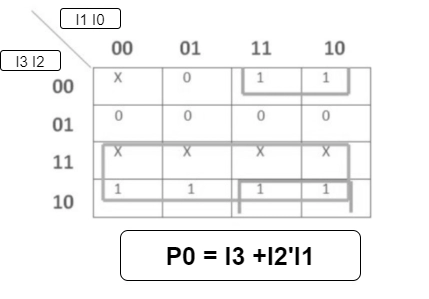
Logical Expression for P1 and P0
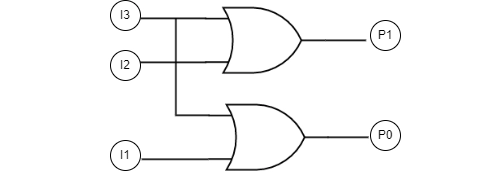
- P1= I3 + I2
-
P0= I3 + I1
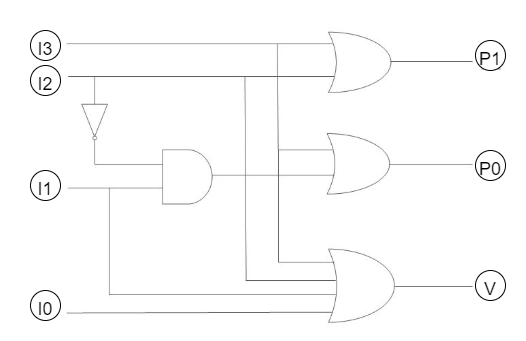
These two Boolean functions P1 and P0 described above can be implemented using two-input OR gates:
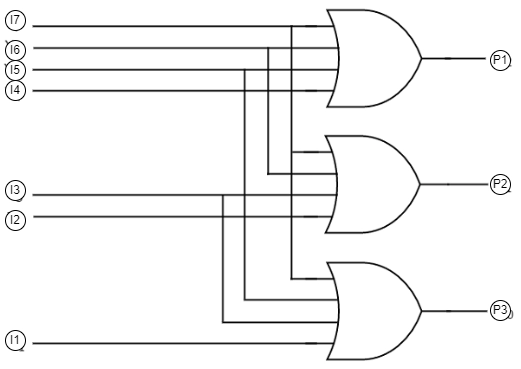
8:3 Encoder
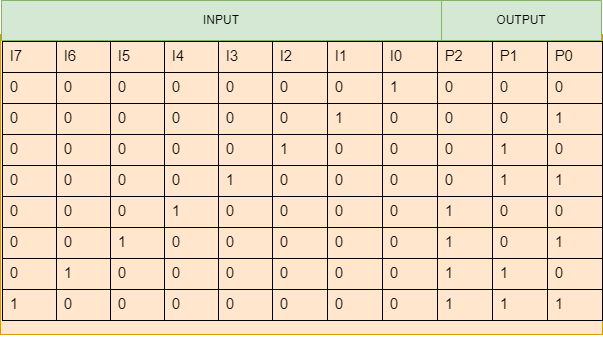
The 8 to 3 Encoder has eight inputs (I7 to I0) and three outputs (P2, P1 and P0). Only one of these eight inputs, which correspond to an octal digit, can be '1' at a time to get the equivalent binary code at the output.

The truth table for the 8:3 encoder is as follows:
Logical Expression for P2, P1 and P0
- P2 = I7 + I6 + I5 + I4
- P1 = I7 + I6 + I3 + I2
-
P0 = I7 + I5 + I3 + I1
These three Boolean functions P2 P1 and P0 described above can be implemented using three-input OR gates: