Equivalence of Functional Dependencies

Introduction

Two or more than two sets of functional dependencies are called equivalence if one set of functional dependencies can be determined using another set of functional dependencies. Similarly,  the later set of Functional dependencies can be derived using the former functional dependency set.

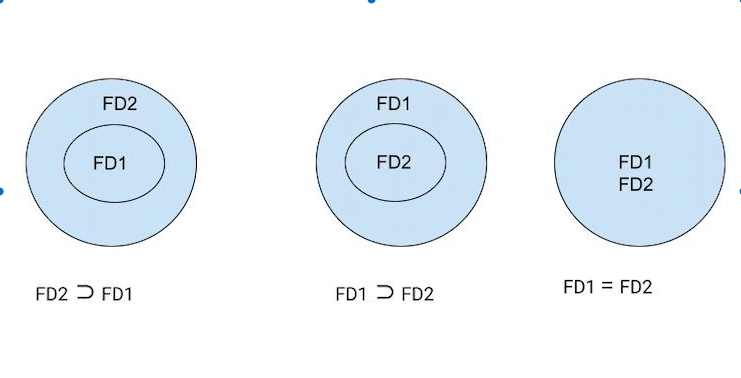
Let F1 and F2 be two FD sets for a relation R 

1. If all FDs of F1 can be derived from FDs present in F2, we can say F2 ⊃ F1.
2. If all FDs of F2 can be derived from FDs present in F1, we can say F1 ⊃ F2.
3. If 1 and 2 both are true, then F1=F2.

                                                      Venn diagram

Also read anomalies in database

Steps to check the equivalence of two different sets of functional dependencies:

Suppose F & G are two sets of FDs in a relational schema R

Check if F covers G

1. Take the functional dependencies of set G into consideration.
2. For each functional dependency X → Y, find the closure of X using the functional dependencies of set G. 
3. Take the functional dependencies of set G into consideration.
4. For each functional dependency X → Y, find the closure of X using the functional dependencies of set F. 
5. Compare the results of both closure sets.
6. If the functional dependencies of set F have determined all those attributes determined by the functional dependencies of set G, then it means F covers G.
7. Thus, we conclude F covers G (F ⊇ G); otherwise, not.

Check if G covers F

1. Take the functional dependencies of set F into consideration.
2. For each functional dependency X → Y, find the closure of X using the functional dependencies of set F.
3. Take the functional dependencies of set F into consideration.
4. For each functional dependency X → Y, find the closure of X using the functional dependencies of set G.
5. Compare the results of both closure sets.
6. If the functional dependencies of set G have determined all those attributes determined by the functional dependencies of set F, then it means G covers F.
7. Thus, we conclude G covers F (G ⊇ F); otherwise, not.

If both F and G cover each other, then they are said to be equivalence functional dependencies. In any other case, they are not equivalent.

Q. ​​Consider another example where two functional dependencies are equivalent.

R=(A,C,D,E,H)

F1={A->C, AC->D, E->AD, E->H},

F2={A->CD, E->AH}

Check whether F1 and F2 are equivalent or not?

Solution:

To check F1 covers F2 −

A+={A,C,D} contains C,D

E+={A,D,E,H} contains A,H

So F1 covers F2

To check F2 covers F1:

A+={A,C,D} contains C

{ A,C}+={A,C,D} contains D

E+={A,C,D,E,H} contains A,D,H

So F2 covers F1.

Hence F1 and F2 are equivalent.

Must Recommended Topic, Schema in DBMS

Frequently Asked Questions

Q1. What is Functional Dependency?

It is a relationship between attributes of a table dependent on each other. For example, If we know the value of student roll number, we can obtain student address, marks, etc. Student address and marks are functionally dependent on student roll number.

Q2. What is the equivalent set of functional dependencies?

Two FDs F and G sets over schema R are equivalent if F⁺ = G⁺. It means that if every functional dependency of F is in G+ and every functional dependence of G is in F+, then we would say that the sets of functional dependencies F and G are equivalent.

Q3. How does functional dependency help normalization?

Functional dependencies are essential in establishing the relationship between key and non-key attributes in a relation. The normalization process removes anomalies in a relation and prevents data redundancy.