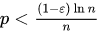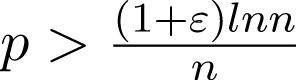Properties of G(n, P) model
The model is named after Hungarian mathematicians Paul Erdős and Alfréd Rényi. In 1960, both mathematicians did an experiment to closely observe the behavior of the G(n, p) model for different values of p. Below are the points that they observed:
-
If np < 1, then a graph will almost have no connected components of size larger than O(log(n)).
-
If np = 1, then a graph will have a largest component whose size is of order n^{2/3}.
-
If np –> c > 1, where c is a constant, then a graph will have a unique giant component containing a positive fraction of the vertices. No other component will contain more than O(log(n)) vertices.
-
If
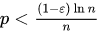, then a graph in G(n, p) will almost surely contain isolated vertices, and thus be disconnected.
-
If
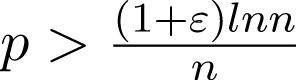, then a graph will be connected.
Implementation
We will be using the below function available in networkx library in python for drawing erdos reyni graph.
Erdos_renyi_graph(n, p, seed=None, directed=False)
Parameters:
n: number of nodes,
p: probability for edge
seed: seed for random number generation, by default it is set to none.
directed: if it's set to true, the graph returned will be a directed graph. By default, its value is set to false
The above function returns a G(n, P) graph created using the values passed.
Code
# importing required libraries
import networkx as nx
import matplotlib.pyplot as plt
# value of n and p
n = 50
P = 0.25
# generating the graph
graph = nx.erdos_renyi_graph(n, P)
# drawing the graph
nx.draw(graph, with_labels=True, node_color="tab:orange")
# showing graph on screen
plt.show()
Output
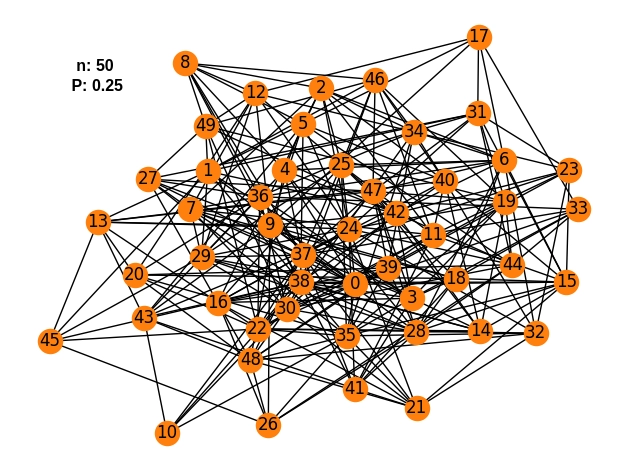
Frequently Asked Questions
What are graphs?
One common type of data structure is a graph, which consists of a finite number of nodes (also called vertices) and a finite number of connected edges. An edge is a pair (u, v) that denotes a connection between u and v vertices.
What are cyclic and acyclic graphs?
If a network has a cycle—a continuous set of nodes without any repeating nodes or edges that connects back to itself—then it is said to be cyclic. Acyclic graphs are those without cycles.
What is the Erdos-Renyi model?
Erdos–Rényi is a model that is used to generate random graphs. We can generate both directed as well as an undirected graphs using this model.
Conclusion
In this article, we have extensively discussed the Erdos-Renyi model that is used to generate random graphs. We have also seen implementation in python.
If you think this blog has helped you enhance your knowledge about the above question, and if you would like to learn more, check out our articles
and many more on our website.
Visit our website to read more such blogs. Make sure that you enroll in the courses provided by us, take mock tests and solve problems and interview puzzles available. Also, you can pay attention to interview stuff- interview experiences and an interview bundle for placement preparations.
Please upvote our blog to help other ninjas grow.
Happy Learning!
. 
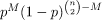38+ registered 