Table of contents

Introduction

Why EM algorithm(Model-Based Algorithm)?

2.1.

The EM Algorithm

2.2.

Applications

2.3.

Key Terms in Expectation-Maximization (EM) Algorithm

How Expectation-Maximization (EM) Algorithm Works

Advantages of the EM Algorithm

Disadvantages of the EM Algorithm

Frequently Asked Questions

6.1.

What is the EM algorithm in machine learning?

6.2.

What are the steps in the EM algorithm?

6.3.

Does the EM algorithm fall into an optimal local state?

6.4.

What are the main applications of the EM algorithm?

Conclusion

Last Updated: Dec 12, 2024

Easy

Expectation-Maximization Algorithm

Author Vamsi Viswanadham

Do you think IIT Guwahati certified course can help you in your career?

Yes

Introduction

The concept of clustering became trendy in the time of Machine Learning development. This concept, clustering, deal with many real-world problems like “Finding Similar kinds of people on Twitter”, “Tag Suggestions,” “Search Engines,” “Customer Segmentation,” etc. The expectation-Maximization Algorithm, popularly known as the EM algorithm, is a Model-based clustering algorithm that tries to optimize the fit between the given data and some mathematical model.

These methods, Model-based clustering methods, basically made an assumption that the data are generated by a mixture of an underlying probability distribution. The EM algorithm is just an extension of the popular k-means partitioning algorithm.

Why EM algorithm(Model-Based Algorithm)?

According to the math, we know that the data is a mixture of probabilistic distributions, where a parametric probability distribution represents each cluster. Here each individual distribution is typically referred to as “component distribution.” The main problem of introducing model-based algorithms or methods is to solve the problem of estimating the probability distributions' parameters to fit the data best.

Example:

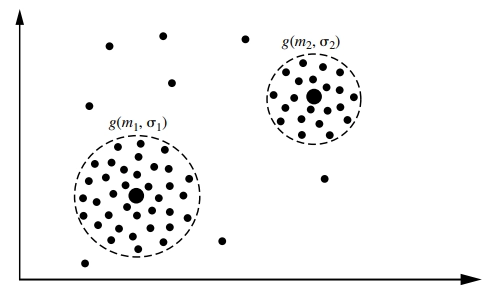
A simple finite mixture density model. The two clusters follow a Gaussian distribution with their own mean and standard deviation.

Reference: Data Mining Concepts and Techniques Second Edition Jiawei Han

The EM Algorithm

The EM Algorithm, Expectation-Maximization Algorithm, is a popular iterative refinement algorithm used for finding the parameter estimates. It is simple and easy to implement. In general, it converges fast and may not lead to generating the global optimal. We said that this algorithm is an extension of k-means. This is because in this EM algorithm, instead of assigning each object to a dedicated cluster, EM gives each object to a cluster according to a weight representing the probability of membership. In other words, there are no strict boundaries between clusters. Therefore, new means are computed based on weighted measures.
The main idea of the EM algorithm is to start with an initial guess estimate of parameters. Then it iteratively rescores the objects against the mixture density produced by the parameter vector. Then the parameter estimates are updated by the use of rescored objects. This can be done in two important steps.

Step-1: Randomly make an initial guess of the parameter vector. In this step, we will randomly select k objects as cluster means or centers and make guesses for additional parameters needed.

Step-2: Update the parameters estimates by using two steps:

(i) Expectation Step:

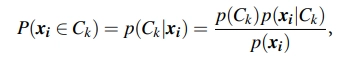
In this step, we will assign each object x_ito cluster C_kwith the above probability, where each probability follows the gaussian distribution with mean m_k and with expectation E_k. Thus we can say that this step will give how probable that each object will belong to a particular cluster. We can say that these probabilities are the expected cluster membership probabilities for object x_i.

(II) Maximization Step: Here, we try to maximize the probabilities of each object belonging to that cluster by re-estimating the model parameters by using

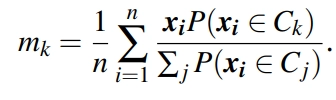
Applications

It has the ability to fill the missing data in a sample.
It can be used as a simple unsupervised data clustering algorithm.
It is frequently used in estimating parameters for mixed models or any other mathematical models. For example, it is estimating the parameters for HMM model.
The fields of image reconstruction and other fields like medicine and structural engineering also use the EM algorithm.

Key Terms in Expectation-Maximization (EM) Algorithm

Latent Variables: Hidden variables that are not directly observed but influence the observed data. The EM algorithm estimates these variables during its iterations.
Expectation Step (E-Step): Computes the expected value of the log-likelihood function using current parameter estimates and observed data.
Maximization Step (M-Step): Maximizes the expected log-likelihood function to update the parameter estimates.
Likelihood Function: Measures how well the model explains the observed data based on the current parameter values.
Convergence: The process of iteratively updating parameters until changes in the log-likelihood or parameters are below a defined threshold.
Initial Parameters: Starting values for the parameters, which influence the speed and outcome of convergence.

How Expectation-Maximization (EM) Algorithm Works

The EM algorithm is an iterative optimization method used for parameter estimation in statistical models with latent variables. Here's how it works:

Initialization: Start with initial guesses for the model parameters. These could be randomly generated or based on prior knowledge.
Expectation Step (E-Step): Use the current parameter estimates to calculate the expected value of the log-likelihood function, considering the latent variables.
Maximization Step (M-Step): Update the parameter estimates by maximizing the expected log-likelihood obtained in the E-step.
Iteration: Repeat the E-step and M-step until the algorithm converges, meaning changes in the log-likelihood or parameters are negligible.
Convergence: Once the algorithm converges, the parameters are considered optimal for the given model and data.

Advantages of the EM Algorithm

Handles Missing Data: The EM algorithm is particularly useful in dealing with datasets containing missing or incomplete data.
Flexibility: It can be applied to various statistical models, including Gaussian Mixture Models and Hidden Markov Models.
Guaranteed Improvement: Each iteration improves the likelihood function, ensuring progress toward convergence.
Robustness: The algorithm works well even when the latent variables are complex or multidimensional.
Numerical Stability: Compared to gradient-based methods, EM avoids issues like divergence due to poor step size choices.

Disadvantages of the EM Algorithm

Slow Convergence: The algorithm may take a large number of iterations to converge, especially for complex models.
Local Optima: EM can get stuck in local optima, particularly if the initial parameter estimates are far from the true values.
Dependence on Initialization: The quality of the final solution heavily depends on the choice of initial parameters.
No Guarantee of Global Optimum: While the log-likelihood improves with each iteration, there is no guarantee that it will reach the global optimum.
Computational Cost: For large datasets or complex models, the E-step and M-step can be computationally expensive.

Frequently Asked Questions

What is the EM algorithm in machine learning?

The Expectation-Maximization algorithm is a model-based clustering algorithm mainly used to estimate the parameter values of a mathematical model. It was developed in 1997 and mainly introduced to find the local maximum likelihood parameters.

What are the steps in the EM algorithm?

EM algorithm mainly contains two steps, and the first step is to initialize the random guess parameters. And in the second step, these parameters are updated by using the Expectation and Maximization steps. These are used to update the variables and update the hypothesis, respectively.

Does the EM algorithm fall into an optimal local state?

As we discussed early, the EM algorithm is an iterative refinement algorithm. Thus it easily falls into the local optima state. The algorithm converges fast and thus may not lead to finding the global optima too.

What are the main applications of the EM algorithm?

The EM algorithm's main applications are filling the missing data, used in data clustering, finding the best latent variables, etc.

Conclusion

In this article, we have mainly discussed the concept of the Expectation-Maximization algorithm, what it is, how it can be used, what are the applications of the EM algorithm, etc.
Hey Ninjas! You can check and explore more unique courses on machine learning concepts through our official website, Coding Ninjas, and checkout Coding Ninjas Studio to learn through articles and other important stuff to your growth.