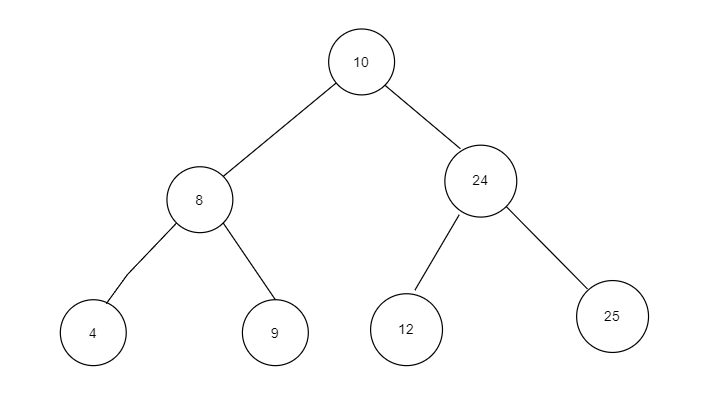
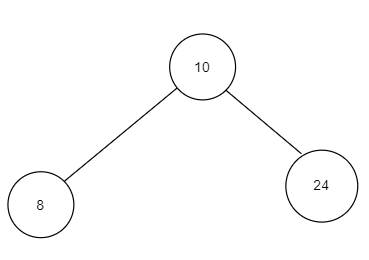
Approach
The approach to the following question is going to be fairly simple. We will use recursion to traverse the tree and once we reach a leaf node, we will remove it from the binary tree and will insert it into our doubly linked list. Also, we will be traversing in the right to left direction, i.e., in the recursive calls, we will first make a call to the right part and then to the left part. You’ll understand the reason for this once you read the algorithm.
Parameters and Function Defined:
- A function named extract() will take the ‘ROOT’ of a binary tree as input and will return the root of the modified tree.
- ‘HEAD’ node, which will be the head of our doubly linked list.
Algorithm
-
Base Case:
- If the ‘ROOT’ is NULL, return NULL.
-
If the ‘ROOT’ is a leaf node:
-
We will be including this node in our doubly linked list and will be removing this from the tree. For that, we will set the right pointer of this node to the previous head of the doubly linked list. Now left of the previous head will be set to the ‘ROOT’ (if the previous head is not NULL).
- Now, ‘ROOT’ will be our new head (this is the reason we are traversing from right to left, and in the end, the node we are left with is going to be our head).
- Return NULL (as we have to delete this node from the tree).
-
If the root is not a leaf node:
- We will make two recursive calls to the same function for the right and left part.
- Return final ‘ROOT’ of the modified tree.
Below is the code for the above algorithm.
Code
#include <iostream>
using namespace std;
// Binary tree node class.
class Node
{
public:
int data;
Node *left, *right;
Node(int data)
{
this->data = data;
this->left = this->right = NULL;
}
};
// Head of the doubly linked list.
Node *headFinal;
// Function to extract the leave nodes in a doubly linked list.
Node *extract(Node *root)
{
// Base Case.
if (root == NULL)
{
return NULL;
}
// Checking if 'ROOT' is a leaf node or not.
if (!root->left && !root->left)
{
// The right pointer of the 'ROOT' node is set to the previous head of the doubly linked list.
root->right = headFinal;
// Left of the previous head is set to 'ROOT'(if it is not NULL).
if (headFinal != NULL)
{
(headFinal)->left = root;
}
// 'ROOT' will be our new head of the doubly linked list.
headFinal = root;
return NULL;
}
// Recursive calls for the remaining tree.
root->right = extract(root->right);
root->left = extract(root->left);
return root;
}
// Printing the pre order traversal of the binary tree.
void printPreOrder(Node *root)
{
if (root == NULL)
{
return;
}
printPreOrder(root->left);
cout << root->data << " ";
printPreOrder(root->right);
}
// Printing the doubly linked list.
void print(Node *head)
{
Node *temp = head;
while (temp != NULL)
{
cout << temp->data << " ";
temp = temp->right;
}
cout << endl;
}
int main()
{
headFinal = NULL;
Node *root = new Node(5);
root->left = new Node(4);
root->right = new Node(6);
root->left->left = new Node(3);
root->right->right = new Node(7);
// Call the extract Function.
root = extract(root);
// Printing the doubly linked list.
cout << "Doubly Linked List: " << endl;
print(headFinal);
// Printing the modified tree.
cout << "Pre order for the modified tree: " << endl;
printPreOrder(root);
return 0;
}

You can also try this code with Online C++ Compiler
Input
5 4 7 6 3
Output
Doubly Linked List
3 7
Pre Order for the modified tree
4 5 6
Note: Input is shown as the pre-order traversal of the tree.
Time Complexity
O(N), where ‘N’ is the number of nodes in the binary tree.
As we are traversing the tree only once thus, the time complexity is O(N).
Space Complexity
O(X), where ‘X’ is the number of leaf nodes present in the binary tree.
As we are making a new doubly linked list of size ‘X’, the space complexity O(X).
Frequently Asked Questions(FAQs)
What is the time complexity of inserting a node in a Binary Search Tree?
The best case time complexity is O(log(N)) where N is the number of Nodes whereas in the case of a skewed BST, the time complexity could be up to O(N)
What is the time complexity of insertion in a Doubly Linked List?
O(N) where N is the size of the Linked List
Conclusion
We saw how we could extract leaf nodes and convert them into a doubly-linked list using recursion. We modified the given tree and removed the leaf nodes as well, and returned the modified tree. Now that you have understood how to extract leaves of a binary tree in a doubly linked list, your confidence on the topic of Binary trees and linked lists would surely be high, but high confidence should not turn into overconfidence, and for that, one needs to practice regularly. But with coding ninjas, you don’t have to worry.
Recommended Reading:
Do check out The Interview guide for Product Based Companies as well as some of the Popular Interview Problems from Top companies like Amazon, Adobe, Google, Uber, Microsoft, etc. on Coding Ninjas Studio.
Also check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, Operating Systems, Computer Networks, DBMS, System Design, etc. as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.
Cheers!