Introduction
This blog will try to strengthen our understanding of a single-dimensional Array data structure problem. We will try to understand how to approach any array data structure problem through that problem. The examples presented will help you clear your concepts, a detailed algorithm will provide you with an immediate solution, and the implementation part will give you a thorough understanding of every step. So, let's get started with the problem statement and some quick examples.
What is Hamming Distance?
The number of locations at which the corresponding characters (elements) differ between two arrays or strings of identical length is known as the Hamming distance. To determine the Hamming distance, count the number of bits that differ between two arrays of the same size. The hamming distance between 1101 and 1001 is 1.
Problem statement
Firstly, we will have a look at what exactly the problem says. Given an array of 'n' elements. In that array, we have to find a rotation with maximum hamming distance.
Sample Examples
Example 1:

Input:
n=5, Array- nums[]= {2,4,5,2,3}
Output:
The maximum hamming distance is: 5
One of the arrays with which the hamming distance would be 5 is {3,5,2,4,2}.
Example 2:
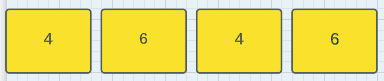
Input:
n=4, Array- nums[]= {4,6,4,6}
Output:
The maximum hamming distance is: 4
One of the arrays with which the hamming distance would be 4 is {6,4,6,4}.Brute Force Approach
In the brute force approach, we create a new array that is twice the size of the old array, with the elements of this new array being the original array's elements repeated twice in the same order. We go through the copy array in each rotation and find the hamming distance.
Algorithm
- Define the size of the array, and take input for the size.
- Define the array of the size taken in input, and take input for the elements of the array.
- We define an array hamm_a[2 * size + 1] and make a copy of the array.
- We initialize a variable for max_value with an initial value 0.
- We loop through the copied array and check for maximum hamming distance.
- The outer loop runs from the first index to (size-1)the index. And in the internal loop, we check for hamming distance.
- We print the result we get while performing the code mentioned above.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
int main()
{ // initializing the size of input array
int size;
cin >> size;
int a[size];
int x = 0;
// input for array elements
for (int i = 0; i < size; i++)
{
cin >> a[i];
}
// making the copy of array
int li = 2 * size + 1;
int hamm_a[li];
for (int i = 0; i < size; i++)
{
hamm_a[i] = a[i];
hamm_a[size + i] = a[i];
}
int max_val = 0;
// outer loop which runs from 1 to the size variable
for (int i = 1; i < size; i++)
{
int Init_val = 0;
int j = i, k = 0;
// inner loop which runs from i to i+size
for (; j < (i + size); j++, k++)
if (hamm_a[j] != a[k])
Init_val++;
if (Init_val == size)
{
cout << "The maximum hamming distance is:" << size << endl;
x = 0;
break;
}
max_val = max(max_val, Init_val);
}
// printing the answer
if (x)
cout << "The maximum hamming distance is: " << max_val << endl;
}
Input:
n=5, a[]={6,7,5,6,4}
Output:
THe maximum hamming distance is: 5
Complexity Analysis
Time Complexity: The time complexity will be O(n^2) as we take two loops one inside another to find the hamming distance.
Space Complexity: The space complexity will be O(n) as we created an extra array to copy array elements.
Also see, Morris Traversal for Inorder and Rabin Karp Algorithm




