Problem
Given a string ‘str’ and a pattern ‘pat’, you have to find all occurrences of the pattern in the string. You have to print the starting positions of all occurrences of the pattern in the string.
Example -
Input:
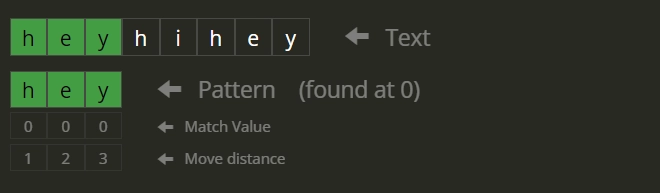
‘str’ = “heyhihey”
‘pat’ = “hey”
Output:
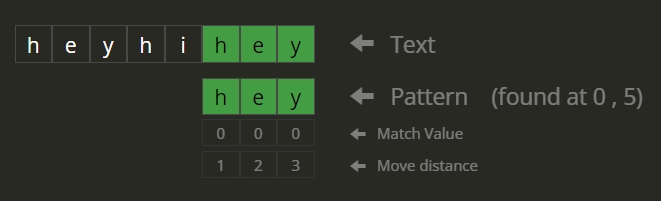
0 5
Explanation:
The pattern in the example is of length 3. Therefore, for every substring of the original string starting from index ‘i’, we have to check if the first three characters of the substring equal the pattern.
- The string starting from index 0 is = “heyhihey”. The first 3 characters of this string are “hey” and are equal to the pattern. Therefore 0 is a valid index.
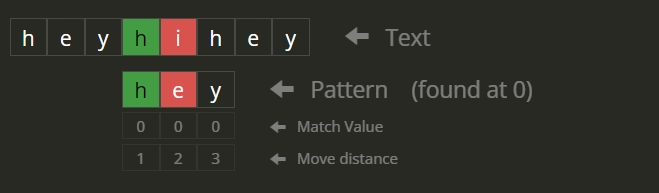
- The string starting from index 1 is = “eyhihey”. The first 3 characters of this string are “eyh” and are not equal to the pattern. Therefore 1 is not a valid index.
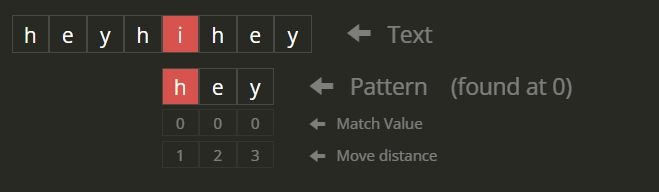
- The string starting from index 2 is = “yhihey”. The first 3 characters of this string are “yhi” and are not equal to the pattern. Therefore 2 is not a valid index.
- The string starting from index 5 is = “hey”. The first 3 characters of this string are “hey” and are equal to the pattern. Therefore 5 is a valid index.
Naive Approach
Let the size of the string be ‘N’ and the size of the pattern be ‘M’. For every index ‘i’ from 0 to ‘N’-1, we iterate over the pattern starting from 0 to ‘M’-1. If every character of the pattern matches the corresponding character of the string, index ‘i’ will be the valid index. After iterating over all ‘i’ from 0 to ‘N’-1, we will have found all occurrences of the pattern in the string.
Implementation
#include<bits/stdc++.h>
using namespace std;
/*
Function to find
All occurrences of the pattern in the string
*/
void solve(string str, string pat){
// Initialising N and M
int n = str.size();
int m = pat.size();
// Iterating over the string
for (int i = 0; i < n; i++){
// Iterating over the pattern
for(int j = 0; j < m; j++){
// If any character mismatches, break
if (i + j >= n || pat[j] != str[i + j]) break;
/*
If we are at the last index,
Print the occurrences of the pattern in the string
*/
if (j == m - 1) cout<<i<<' ';
}
}
cout<<endl;
}
// Driver Code
int main(){
string str = "heyhihey";
string pat = "hey";
solve(str, pat);
}Output
0 5Time Complexity
We are using a nested loop to first iterate over the string (size = N) and then for each index, we are iterating over the pattern (size = M). Therefore the time complexity of the approach is O(N * M).
Space Complexity
We are just using a few extra variables therefore the space complexity of the above approach is O(1).