Algorithm🧑🏻💻
👉🏻 At first, we have to declare a map and set one of its arguments as a boolean.
👉🏻 Store all the values of the given array with "true" boolean values into the map by traversing the original array.
👉🏻 Define a boolean variable with the name ‘foundPair’ and set its value to "false".
👉🏻 Traverse the given array from ‘0’ to ‘n-1’, where ‘n’ is the array's length.
- Now we have to check if ‘k’ has an entry in the map and whether ‘k’ is smaller than the current array element or not. If true, print the ‘k’ and the array element value. Then set the boolean value to "true".
- Check if the value of ‘k’ is less than or equal to the current element of the array. If "true", create a vector and then find all the divisors of the array[i]-k value and store it into the vector.
- Now traverse the vector we created in the previous step and we’ve to check if that element of a vector and the element of the array are pair that satisfies the given condition when modulo is done.
-
Print the vector and the current array element and set the Boolean value to "true".
👉🏻 Return ‘foundPair’.
Implementation In C++💻
C++ code for the problem statement find all pairs (a, b) in an array such that a % b = k.
#include<math.h>
#include <unordered_map>
#include<iostream>
#include<vector>
using namespace std;
vector<int> findPossibleDiv(int n)
{
vector<int> vecDiv;
for (int j = 1; j <= sqrt(n); j++)
{
if (n % j == 0)
{
if (n / j == j)
vecDiv.push_back(j);
else
{
vecDiv.push_back(j);
vecDiv.push_back(n / j);
}
}
}
return vecDiv;
}
bool pairModulousK(int array[], int n, int k)
{
unordered_map<int, bool> MAP;
for (int i = 0; i < n; i++)
MAP[array[i]] = true;
bool foundPair = false;
for (int i = 0; i < n; i++)
{
if (MAP[k] && k < array[i])
{
cout << "(" << k << ", " << array[i] << ") ";
foundPair = true;
}
if (array[i] >= k)
{
vector<int> vec = findPossibleDiv(array[i] - k);
for (int j = 0; j < vec.size(); j++)
{
if (array[i] % vec[j] == k && array[i] != vec[j] && MAP[vec[j]])
{
cout << "(" << array[i] << ", "<< vec[j] << ") ";
foundPair = true;
}
}
vec.clear();
}
}
return foundPair;
}
int main()
{
int array[] = {5, 4, 6, 7, 3};
int n = sizeof(array) / sizeof(array[0]);
int k = 3;
if (pairModulousK(array, n, k) == false)
cout << "There is no such pair.";
return 0;
}

You can also try this code with Online C++ Compiler
Output -
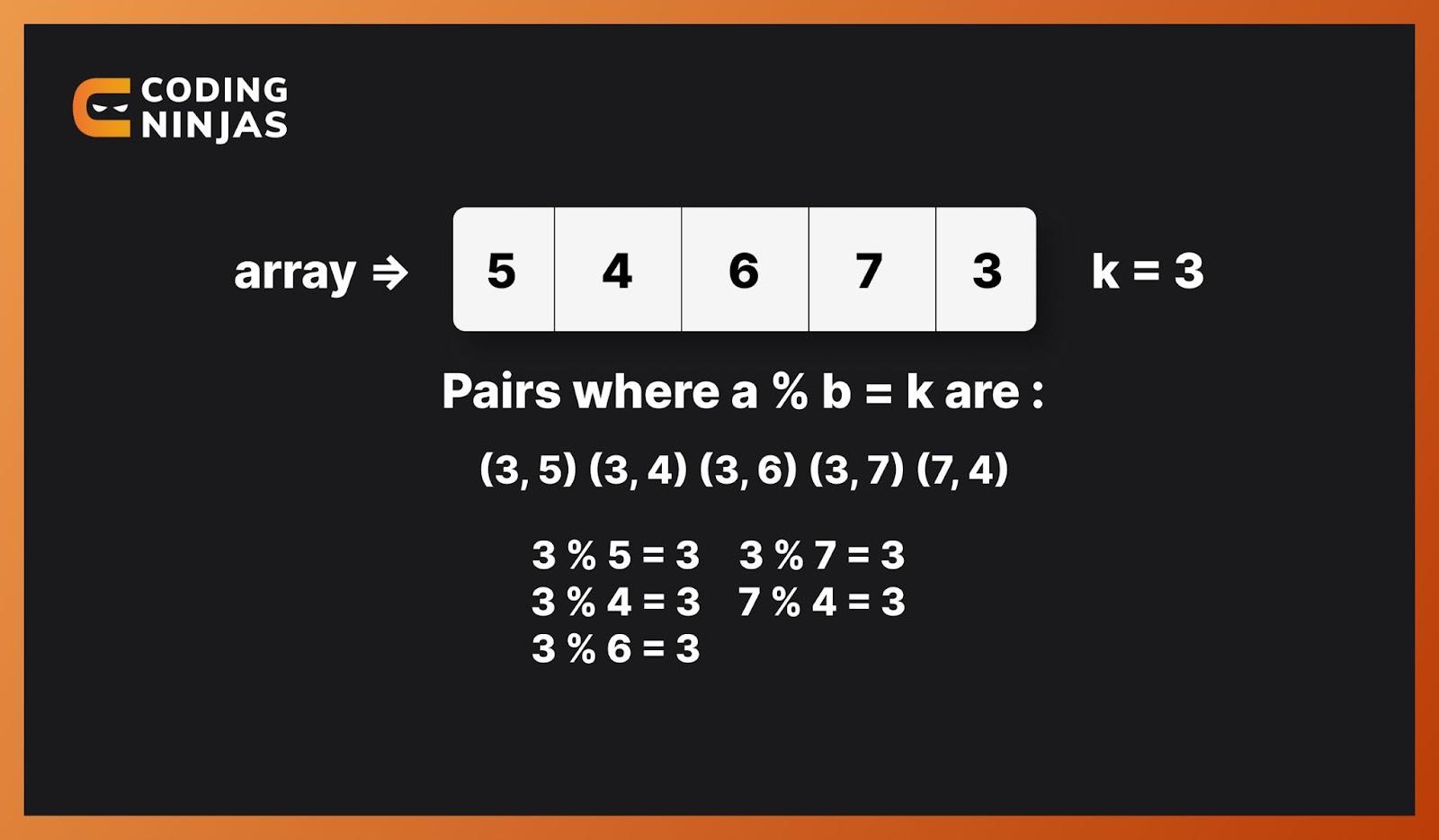
(3, 5) (3, 4) (3, 6) (3, 7) (7, 4)
You can also read about the Longest Consecutive Sequence.
Implementation In Java💻
Java code for the problem statement find all pairs (a, b) in an array such that a % b = k.
import java.util.HashMap;
import java.util.Vector;
class Test {
static Vector<Integer> findTheDivisors(int n)
{
Vector<Integer> v = new Vector<>();
for (int j = 1; j <= Math.sqrt(n); j++)
{
if (n % j == 0)
{
if (n / j == j)
v.add(j);
else
{
v.add(j);
v.add(n / j);
}
}
}
return v;
}
static boolean printThePairs(int array[], int n, int k)
{
HashMap<Integer, Boolean> occ = new HashMap<>();
for (int i = 0; i < n; i++)
occ.put(array[i], true);
boolean foundPair = false;
for (int i = 0; i < n; i++)
{
if (occ.get(k) && k < array[i])
{
System.out.print("(" + k + ", " + array[i] + ") ");
foundPair = true;
}
if (array[i] >= k)
{
Vector<Integer> v = findTheDivisors(array[i] - k);
for (int j = 0; j < v.size(); j++)
{
if (array[i] % v.get(j) == k && array[i] != v.get(j) && occ.get(v.get(j)))
{
System.out.print("(" + array[i] + ", "
+ v.get(j) + ") ");
foundPair = true;
}
}
v.clear();
}
}
return foundPair;
}
public static void main(String args[])
{
int array[] = {5, 4, 6, 7, 3};
int k = 3;
if (printThePairs(array, array.length, k) == false)
System.out.println("There is no such pair exists.");
}
}

You can also try this code with Online Java Compiler
Output -
(3, 5) (3, 4) (3, 6) (3, 7) (7, 4)
Implementation In Python💻
Python code for the problem statement find all pairs (a, b) in an array such that a % b = k.
import math as mt
def findTheDivisors(n):
v = []
for i in range(1, mt.floor(n**(.5)) + 1):
if (n % i == 0):
if (n / i == i):
v.append(i)
else:
v.append(i)
v.append(n // i)
return v
def printThePairs(array, n, k):
occ = dict()
for i in range(n):
occ[array[i]] = True
foundPair = False
for i in range(n):
if (occ[k] and k < array[i]):
print("(", k, ",", array[i], ")", end = " ")
foundPair = True
if (array[i] >= k):
v = findTheDivisors(array[i] - k)
for j in range(len(v)):
if (array[i] % v[j] == k and
array[i] != v[j] and
occ[v[j]]):
print("(", array[i], ",", v[j],
")", end = " ")
foundPair = True
return foundPair
array = [5, 4, 6, 7, 3]
n = len(array)
k = 3
if (printThePairs(array, n, k) == False):
print("There is no such pair exists.")

You can also try this code with Online Python Compiler
Output -
(3, 5) (3, 4) (3, 6) (3, 7) (7, 4)
Check out this array problem - Merge 2 Sorted Arrays
Complexities of Algorithm🎯
The time and space complexity of the given solution for the problem statement to find all pairs (a, b) in an array such that a % b = k are given below.
Time Complexity
The time complexity is O (n * sqrt(max)) where ‘max’ is the maximum element of the array.
We used the following fact for all the elements that are greater than or equal to k-
If arr[i] % arr[j] = k,
==> arr[i] = x * arr[j] + k
==> (arr[i] - k) = x * arr[j]
We found the divisor of (array[i] - k) and checked if they are present in array[] by using hashing.
Space Complexity
The space complexity is O(n), where ‘n’ is the length of the given array. We need this space to store the element in the hash map.
Frequently Asked Questions🤔
What is hashing?
In the data structure, hashing is a technique of mapping a large part of data into small tables using a hashing function.
What is an array?
An array stores similar data type elements and has a fixed size. It stores elements in the contagious memory location, which means there is no space between the elements of an array in the memory location.
What is modulo?
In number theory, it is a symbol/operator (%) used to find the modulus of a number. Modulus is the remainder we get on dividing a number with another number.
What are all pairs (a, b) in an array {5, 4, 6, 7, 3} such that a % b = k where k = 2?
The pairs that satisfy the condition are (5, 3) (6, 4) (7, 5).
What is Boolean?
A data type called boolean has two possible values to assign, which are also called truth values that are "true" and "false".
Conclusion
In this blog, we went through the solution to the problem statement to find all pairs (a, b) in an array such that a % b = k using hashing. We also discussed the Algorithm of the solution and then understood the code and its complexities if you would like to learn more, check out our articles on Count quadruples from four sorted arrays whose sum is equal to a given value x and Count Divisible Pairs in an Array.
Recommended problems -
Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc. Enroll in our courses and refer to the mock test and problems available. Take a look at the interview experiences and interview bundle for placement preparations.
Do upvote our blog to help other ninjas grow.

Happy Learning Ninja!