Problem Statement🕵️♂️
We have given an undirected graph and a set of vertices. We have to find all reachable nodes from every node present in a given set.
Input: An integer array ‘arr’ where arr contains the number of nodes.
Output: All the reachable nodes from a given vertex.
Example
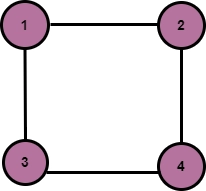
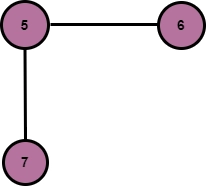
Consider above an undirected graph with two disconnected components.
Input: array[ ] = { 1, 3, 5 }
Output:
Reachable nodes from node2 are 1, 2, 3, and 4.
Reachable nodes from node3 are 1, 2, 3, and 4.
Reachable nodes from node5 are 5, 6, and 7.
Approach👩💻
📝 Simple Approach
-
A simple approach to solve this problem is to perform a BFS traversal for every node present in the Set and find all the reachable nodes.
-
But the problem with BFS traversal is that we have to call BSF separately for each node without using the visited array of the last traversal because this same vertex will be printed multiple times.
-
The time complexity will be O(n * (V + E)). This approach is appropriate, but when E = Θ(V2) and n = V, time complexity becomes O(V3), in which E is the no. of edges in a graph and V is the number of nodes in the graph.
📝Optimistic Approach
-
As the graph is undirected, all the nodes belonging to similar components will have the same reachable nodes. Therefore, we will keep track of the mapping of nodes and components.
-
Each component in a graph has a number, and each node in this component has this number.
-
For this, we use a visited array to keep note of visited nodes in BFS.
For node x,
If visited[x] is 0, then
x is unvisited.
else
Visited[x] represents the component number.
-
For any two nodes, say 'x' and 'y' if they belong to the same component, then visited[x] == visited [y].
-
For storing reachable nodes, we will use map 'm' with its key as a component number and value as a vector to keep all the reachable nodes.
-
For finding reachable nodes for node x return m[visited[x]].
Pseudocode:
componentNumber = 0
for i=1 to n
If visited[i] is NOT 0 the
componentNumber++
/* function BFS() returns a list
for given node ‘i’ */
List = BFS(i, componentNumber)
m[visited[i]] = list
Solution
Let us look for the solution for finding all reachable nodes from every node present in a given set.
💥C++
#include <bits/stdc++.h>
using namespace std;
/* This class represents a directed graph using
adjacency list representation */
class UGraph
{
public:
int V; // No. of vertices
/* Pointer to an array containing adjacency lists */
list<int> *adj;
UGraph(int ); // Constructor
void insert_edge(int, int);
vector<int> BFS(int, int, int []);
};
UGraph::UGraph(int V)
{
this->V = V;
adj = new list<int>[V+1];
}
void UGraph::insert_edge(int x, int y)
{
adj[x].push_back(y); // Add w to y’s list.
adj[y].push_back(x); // Add y to w’s list.
}
vector<int> UGraph::BFS(int componentNumber, int src,
int visited[])
{
/* Mark all the vertices as not visited
Create a queue for BFS */
queue<int> queue;
queue.push(src);
/* Assign Component Number */
visited[src] = componentNumber;
/* Vector to keep all the reachable nodes from 'src' */
vector<int> reachableNodes;
while(!queue.empty())
{
/* Dequeue a vertex from queue */
int x = queue.front();
queue.pop();
reachableNodes.push_back(x);
/* Get all adjacent vertices of the dequeued
vertex u. If an adjacent has not been visited,
then mark it visited and enqueue it */
for (auto itr = adj[x].begin();
itr != adj[x].end(); itr++)
{
if (!visited[*itr])
{
/* Assign Component Number to all the
reachable nodes */
visited[*itr] = componentNumber;
queue.push(*itr);
}
}
}
return reachableNodes;
}
/* show all the Reachable Nodes from a node 'n' */
void showReachableNodes(int n,
unordered_map <int, vector<int> > m)
{
vector<int> tmpr = m[n];
/* for loop */
for (int i=0; i<tmpr.size(); i++)
cout << tmpr[i] << " ";
/* printing*/
cout << endl;
}
/* search all the reachable nodes for each element
in the arr */
void findReachableNodes(UGraph ug, int arr[], int n)
{
/* Get the no. of nodes in the graph */
int V = ug.V;
/* Take an integer visited array and initialize
all the elements with 0 */
int visited[V+1];
memset(visited, 0, sizeof(visited));
/* Map to store a list of reachable Nodes for a
given node. */
unordered_map <int, vector<int> > m;
/* Initialize component Number with 0 */
int componentNumber = 0;
/* For each node in arr[] find reachable
Nodes */
for (int i = 0 ; i < n ; i++)
{
int x = arr[i];
/* Visit all the nodes of the component */
if (!visited[x])
{
componentNumber++;
/* Store the reachable Nodes corresponding to
the node 'i' */
m[visited[x]] = ug.BFS(componentNumber, x, visited);
}
/* Now, we have all reachable nodes
from x; print them by looking up in map m. */
cout << "Reachable Nodes from " << x <<" are\n";
showReachableNodes(visited[x], m);
}
}
/* main */
int main()
{
/* Create a graph given in the diagram above */
int V = 7;
UGraph ug(V);
ug.insert_edge(1, 2);
ug.insert_edge(2, 3);
ug.insert_edge(3, 4);
ug.insert_edge(3, 1);
ug.insert_edge(5, 6);
ug.insert_edge(5, 7);
/* For every ith element in the arr
find all reachable nodes from query[i] */
int arr[] = {2, 3, 7};
/* Find the number of elements in Set */
int n = sizeof(arr)/sizeof(int);
findReachableNodes(ug, arr, n);
return 0;
}

You can also try this code with Online C++ Compiler
Output:
Reachable Nodes from 2 are
2 1 3 4
Reachable Nodes from 3 are
2 1 3 4
Reachable Nodes from 7 are
7 5 6
💥Python
from collections import deque
def insert_edge(x, y):
global visited, adj
adj[x].append(y)
adj[y].append(x)
def BFS(componentNumber, src):
global visited, adj
# Mark all the vertices as not visited
# Create a queue for BFS
#a = visited
queue = deque()
queue.append(src)
# Assign Component Number
visited[src] = 1
# Vector to store all the reachable
# nodes from 'src'
reachableNodes = []
#print("0:",visited)
while (len(queue) > 0):
# Dequeue a vertex from queue
u = queue.popleft()
reachableNodes.append(u)
# Get all adjacent vertices of the dequeued
# vertex u. If an adjacent has not been visited,
# then mark it visited and enqueue it
for itr in adj[u]:
if (visited[itr] == 0):
# Assign Component numbers to all the
# reachable nodes
visited[itr] = 1
queue.append(itr)
return reachableNodes
# Display all the Reachable Nodes
# from a node 'n'
def showReachableNodes(m):
for i in m:
print(i, end = " ")
print()
# search reachable nodes
def findReachableNodes(arr, n):
global V, adj, visited
# Get the no. of nodes in the graph
# Map to store the list of reachable Nodes for a
# given node.
a = []
# Initialize component Number with 0
componentNumber = 0
# For each node in arr[], find reachable
# Nodes
for i in range(n):
x = arr[i]
# Visit all the nodes of the component
if (visited[x] == 0):
componentNumber += 1
# Store the reachable Nodes corresponding
# to the node' i'
a = BFS(componentNumber, x)
# Now, we have all reachable nodes
# from x, print them by doing a lookup in map m.
print("Reachable Nodes from ", x, " our")
showReachableNodes(a)
# main
if __name__ == '__main__':
#declaring
V = 7
adj = [[] for i in range(V + 1)]
#visited node
visited = [0 for i in range(V + 1)]
insert_edge(1, 2)
insert_edge(2, 3)
insert_edge(3, 4)
insert_edge(3, 1)
insert_edge(5, 6)
insert_edge(5, 7)
# For every ith element in the arr
# find all reachable nodes from query[i]
arr = [ 2, 3, 7 ]
# Find a number of elements in Set
n = len(arr)
findReachableNodes(arr, n)

You can also try this code with Online Python Compiler
Output:
Reachable Nodes from 2 our
2 1 3 4
Reachable Nodes from 3 our
2 1 3 4
Reachable Nodes from 7 our
7 5 6
💥Complexities
✳️Time complexity:
-
For finding all reachable nodes from every node present in a given set, the Time complexity will be O(V+E). Where V is the no. of nodes, E is the number of edges and n is the size of a given set.
-
In the worst case, all the V nodes are shown for each node, meaning only one component is present in the graph, so it will take O(n*V). The worst Time complexity for finding all reachable nodes from every node present in a given set is O(V+E) + O(n*V).
✳️Space complexity: Space complexity for finding all reachable nodes from every node present in a given set will be O(V).
Frequently Asked Questions
What is Graph?
A graph data structure is a non-linear data structure that contains two non-empty sets of vertices and edges.
Why are graphs important data structures?
Because they can easily represent the relations between real-life data.
What does a reachable node mean?
When two nodes are connected directly, they are known as reachable nodes.
What is the time complexity to find all reachable nodes from every node present in a given set?
For finding all reachable nodes from every node present in a given set, the Time complexity will be O(V+E). Where V is the no. of nodes, E is the number of edges and n is the size of a given set.
What is BFS traversal?
BFS stands for Breadth-First Search. BFS is an algorithm for searching or traversing tree or graph data structures.
Conclusion
In this article, we have discussed the solution to find all reachable nodes from every node present in a given set. We started with the problem statement, then saw examples to understand, then the approach, and finally, the solution.
Can you now solve Cycle detection in an undirected graph?
You can check out some articles related to this topic as well:
Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc. Enroll in our courses and refer to the mock test and problems available. Take a look at the interview experiences and interview bundle for placement preparations.
Happy learning, Ninja🥷







