Introduction
This article will look at a problem of common elements in three sorted arrays. Array-based questions are the most popular and vital in coding interviews and programming competitions.
Let's understand the problem statement.
Problem Statement
We have given three sorted arrays of sizes N1, N2, and N3, respectively, and we have to find the common elements in three sorted arrays.
Here first, we will discuss the brute force approach and then the optimized method.
Sample Examples
Example 1:
Input:
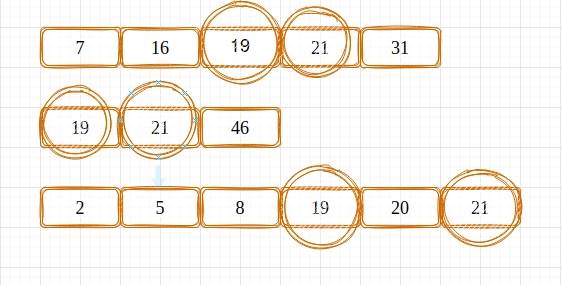
ar1[] = {7, 16, 19, 21, 31}
ar2[] = {19, 21, 46}
ar3[] = {2, 5, 8, 19, 20, 21}
Output:
20, 80
Example 2:
Input:
ar1[] = {1, 2, 2}
ar2[] = {2, 2, 6, 7, 10}
ar3[] = {1, 2, 2, 20}
Output:
2, 2
Brute Force Approach
The most straightforward approach is to use three for loops to find common elements in three sorted arrays.
- Using three for loops, produce all possible combinations of triplets (one from each input array) and check if they are equal.
- This approach is not utilizing the fact that input arrays are sorted.
Pseudocode
For i=0, i<= size of array1, i+=1{
For j = 0, j<= size of array2, j+=1{
For k =0, k<=size of array3, k+=1{
If array[1] and array[2] and array[3] are equal
Then print the element
}
}
}Implementation in C++
#include <bits/stdc++.h>
using namespace std;
void find_Common_Elements(int arr1[], int arr2[], int arr3[], int n1,
int n2, int n3)
{
for(int i = 0; i < n1; i++) {
for(int j = 0; j < n2; j++) {
for(int k = 0; k < n3; k++) {
if(arr1[i] == arr2[j] && arr2[j] == arr3[k]) {
cout<<(arr1[i])<<" ";
}
}
}
}
}
// Driver code
int main()
{
int arr1[] = {7, 16, 19, 21, 31} ;
int arr2[] = {19, 21, 46} ;
int arr3[] = {2, 5, 8, 19, 20, 21};
int n1 = sizeof(arr1) / sizeof(arr1[0]);
int n2 = sizeof(arr2) / sizeof(arr2[0]);
int n3 = sizeof(arr3) / sizeof(arr3[0]);
cout << "Common Elements in three sorted arrays are ";
find_Common_Elements(arr1, arr2, arr3, n1, n2, n3);
return 0;
}
Output:
Common Elements in three sorted arrays are 19 21
Complexity Analysis
Time Complexity: O(n1*n2*n3)
We are using three loops in this approach; check if all feasible triplet combinations (one from each input array) are equivalent, if they are equal means we find the common elements in three sorted arrays
Space Complexity: O(1)
No extra space is used.




