Find duplicates in a given array when elements are not limited to a range

Introduction 

In this article, we will  find the duplicate number in a limited range array of size n with elements between 1 and n-1. 

Now let us understand the concept of finding duplicates with the help of an example.

Approach: Using Hashing

As we know, a data structure that associates values with keys is known as a hash table. This calculates key indexes using a hash function. We can store the value at the proper location based on the Hash Table index.

Now that you've devised a concept, let's look at its algorithm and implementation:

Approach: Use unordered_map for hashing

Count the number of times each element appears, and the elements with a frequency greater than one are printed. Because the range of numbers is unknown, unordered_map is used. 

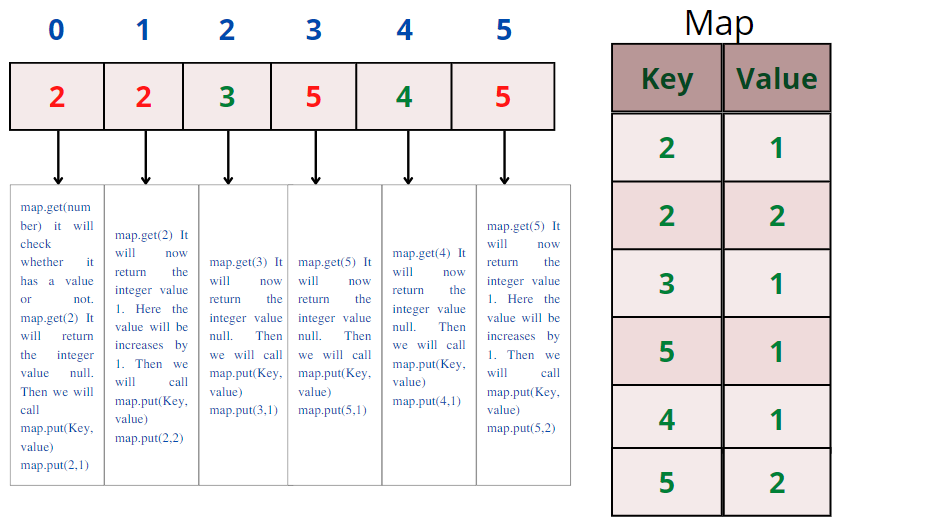
Implementation in Java

/*Java program to find duplicates in the array given*/
import java.util.HashMap;
import java.util.Map;
import java.util.Map.Entry;
 
public class Main
{
    // Driver program
    public static void main(String[] arg)
    {
        int array[] = {11, 10, 40, 11, 7, 9, 5, 40, 11};
        int n = array.length;
        printingDuplicates(array, n);
    }
    //finding and printing duplicates
    private static void printingDuplicates(int[] array, int n)
    {
        Map<Integer,Integer> map = new HashMap<>();
        int count = 0;
        boolean dupl = false;
        for(int i = 0; i < n; i++){
            if(map.containsKey(array[i])){
                count = map.get(array[i]);
                map.put(array[i], count + 1);
            }
            else{
                map.put(array[i], 1);
            }
        }
         
        for(Entry<Integer,Integer> entry : map.entrySet())
        {
            /* if the frequency is greater than 1
            printing the element */
            if(entry.getValue() > 1){
                System.out.print(entry.getKey()+ " ");
                dupl = true;
            }
        }
        // if no duplicates are present
        if(!dupl){
            System.out.println("-1");
        }
    }
}

You can also try this code with Online C Compiler

Run Code

Output 

Implementation in C++

#include <bits/stdc++.h>
using namespace std;
 
// function duplicates to find and print
void Duplicates(int arry[], int n)
{
    // using unordered_map to store frequencies
    unordered_map<int, int> freqc;
    for (int i=0; i<n; i++)
        freqc[arry[i]]++;
 
    bool dupl = false;
    unordered_map<int, int>:: iterator itr;
    for (itr=freqc.begin(); itr!=freqc.end(); itr++)
    {
        // if the frequency is more than 1 print element
        if (itr->second > 1)
        {
            cout << itr->first << " ";
            dupl = true;
        }
    }
 
    //If duplicates are not present
    if (dupl == false)
        cout << "-1";
}
 
// to test the driver program
int main()
{
    int arry[] = {7, 18, 10, 10, 7, 6, 11, 12, 11};
    int n = sizeof(arry) / sizeof(arry[0]);
    Duplicates(arry, n);
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output 

Implementation in Python3

To store a number as a key and its frequency as a value in Python, use a dictionary. Because the range of integers is unknown, a dictionary can be used.

# Python3 program for finding duplicates
# by using a dictionary approach.
def printingDuplicates(arry):
    dict = {}
 
    for elem in arry:
        try:
            dict[elem] += 1
        except:
            dict[elem] = 1
             
    for itm in dict:
         
         # if the frequency is greater than 1
         # then printing  the element
        if(dict[itm] > 1):
            print(itm, end=" ")
 
    print("\n")
 
# Driver Code
if __name__ == "__main__":
    list = [13, 13, 11, 6,
            2, 6, 5, 12, 11]
    printingDuplicates(list)

Output

Implementation in C#

/* C# program for finding the duplicates in given array*/
using System;
using System.Collections.Generic;
 
class findingDuplicates
{
    // function for finding and printing duplicates
    static void printingDuplicates(int[] arry, int n)
    {
        Dictionary<int,
                   int> map = new Dictionary<int,
                                             int>();
        int count = 0;
        bool dupl = false;
        for (int i = 0; i < n; i++)
        {
            if (map.ContainsKey(arry[i]))
            {
                count = map[arry[i]];
                map[arry[i]]++;
            }
            else
                map.Add(arry[i], 1);
        }
 
        foreach (KeyValuePair<int,
                              int> entry in map)
        {
            // if the frequency is greater than 1
            // printing the element
            if (entry.Value > 1)
                Console.Write(entry.Key + " ");
            dupl = true;
        }
 
        // if no duplicates found
        if (!dupl)
            Console.WriteLine("-1");
    }
 
    // Driver Code
    public static void Main(String[] arg)
    {
        int[] arry = { 3, 4, 4, 7,
                     5, 4, 5, 1, 1 };
        int n = arry.Length;
        printingDuplicates(arry, n);
    }
}

Output 

The above solution has time complexity O(N) and auxiliary space is  O(N)

You can also read about the Longest Consecutive Sequence.