Introduction
The binary tree is one of the most important topics required for interview preparation. Many companies, including the MAANG, ask questions from binary trees in the technical rounds and interviews. Since this topic is important, it becomes necessary to practice it thoroughly.
To help you solve problems on binary trees, we will be discussing a simple problem of binary trees. The problem is to find if there is a pair in root to a leaf path with a sum equal to the root's data. But before discussing the problem, let's first understand what a binary tree is.
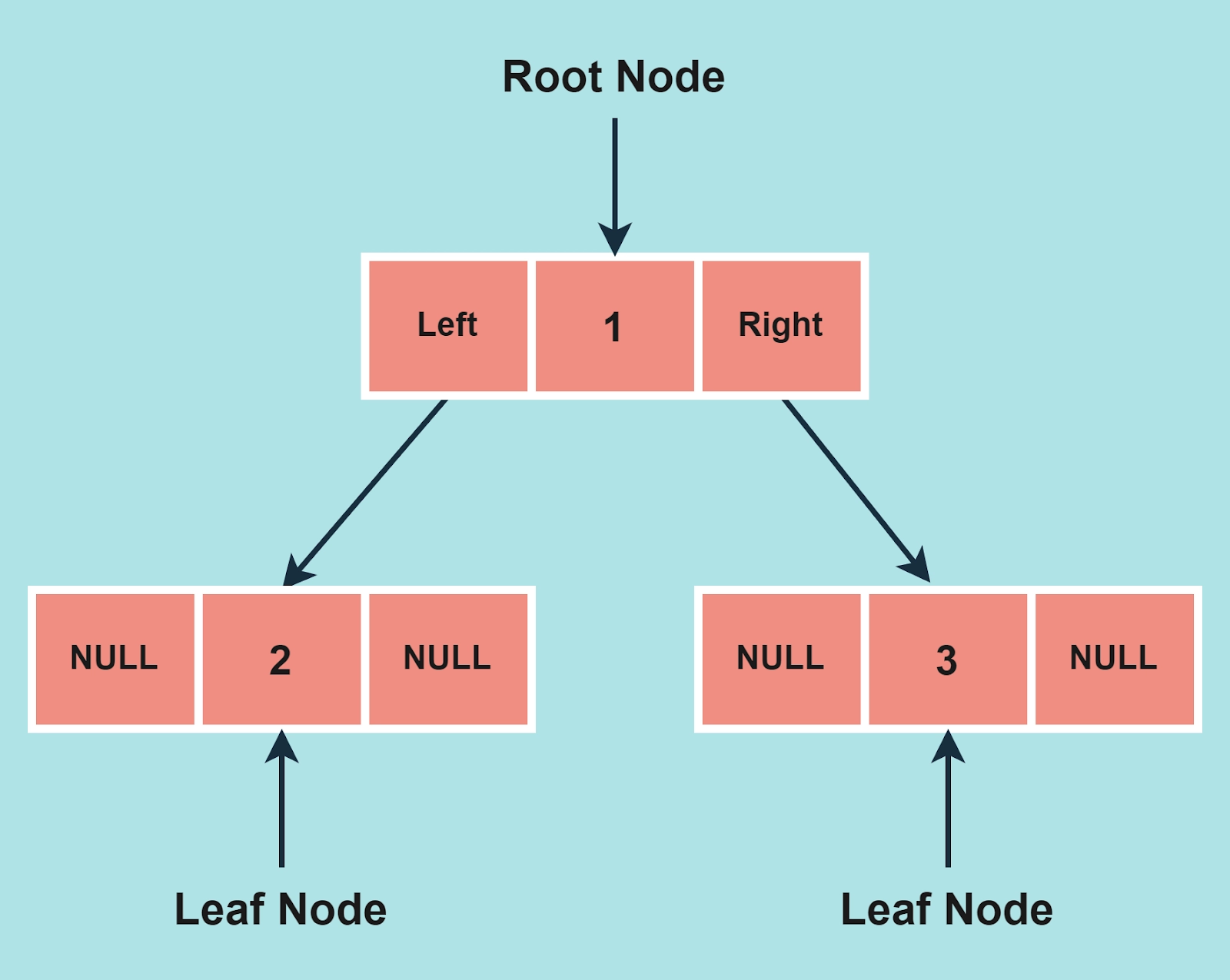
Binary tree
A binary tree is a tree data structure in which each node has at most two children, which are known as the left and right children.
Each node in a binary tree has a "left" pointer, a "right" pointer, and a data element. The "root" pointer points to the tree's topmost node. The left and right pointers point to smaller "subtrees" on either side. A null pointer symbolizes the empty tree, a binary tree with no children.
Problem Statement
Ninjas have a binary tree. The binary tree has n nodes in it. He gave the binary tree to us and said that we have to find if there is a pair in root to a leaf path with a sum equal to the root's data. But, the problem is that he cannot find the pair by himself he is busy with some other work. Can you help him with the problem?
You need to print Yes if there is pair in root to a leaf path with a sum equal to the root's data. Else, print No.
Before deep-diving into the solution to this problem, we should look at some examples to help us understand the problem better.
Some Examples
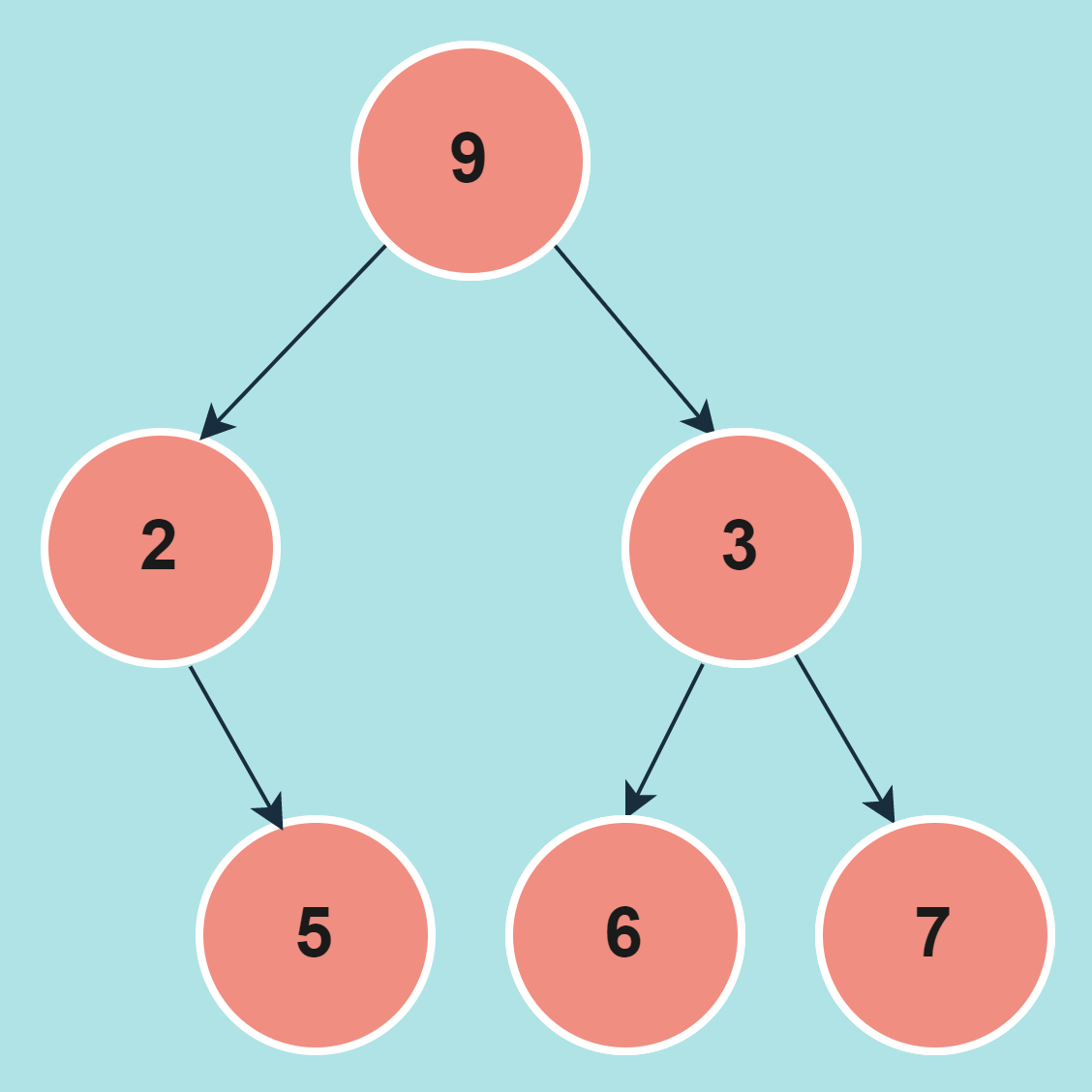
Input:
Tree:
Output:
Yes
Explanation:
The root to a leaf path {9,3,6} consists of the pair {3,6} whose sum is equal to 9, equal to the root's value.
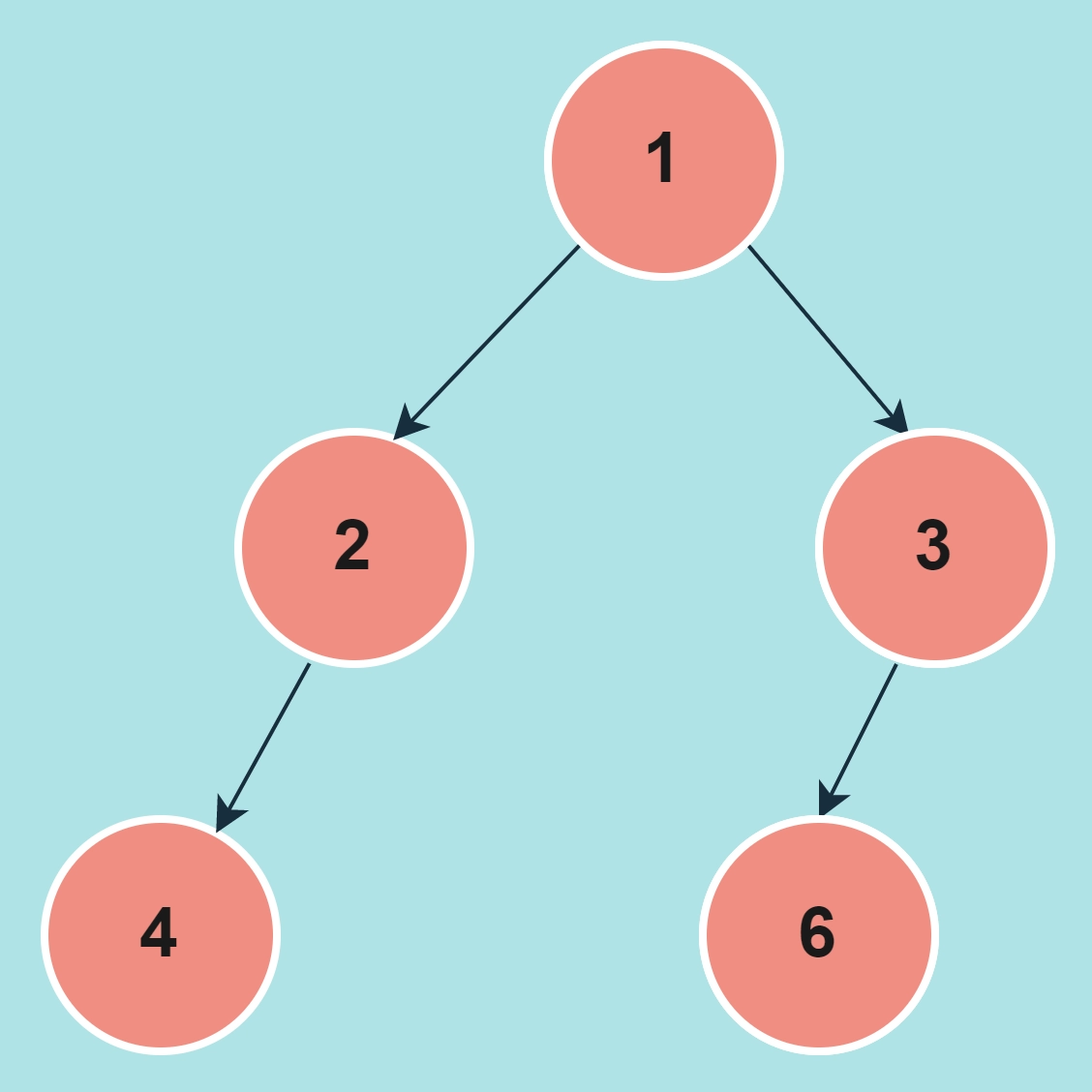
Input:
Tree:
Output:
No
Explanation:
There is no root to a leaf path having a pair with a sum equal to the root's data.
Approach
The approach to solving this problem of finding a pair in root to a leaf path with a sum equal to the root's data is quite straightforward. In this approach, we will store every node's value in the map. And at every point, we will check if a value is equal to (rootValue-currentNode) in the map. If it exists, we will return true else; continue. We will return false if we reach any node having a NULL value.
Algorithm
1. To solve this problem, we will create a boolean function called doesPairExist(), and in the main function, we will make two function calls for this function, one for the left subtree and another for the right subtree.
2. While traversing the tree, we will return false if the node becomes NULL.
3. We will check for the following condition:
if (m.find(rootValue - root->data) != m.end())
return true;
4. Here root value is the value of the root node, and the root->data is the value of the current node of the tree.
5. Now, we will increment the current node's value in the map.
6. After incrementing the current node's value, we will make two recursive calls.
// checking for left subtree
bool left = doesPairExist(root->left, m, rootValue);
// check for right subtree
bool right = doesPairExist(root->right, m, rootValue);
7. After making these two recursive calls, we will decrease the current node's value from the map.
8. In the end, we will return the OR value of the left and right. So that if one of the calls returns true, we will return true to the main function.
Code in C++
// C++ code to find if there is a pair in root to a leaf path with a sum equal to the root’s data
#include <bits/stdc++.h>
using namespace std;
struct Tree
{
int data;
Tree *left;
Tree *right;
Tree(int x) : data(x), left(NULL), right(NULL) {}
};
bool doesPairExist(Tree *root, unordered_map<int, int> m, int rootValue)
{
if (!root)
return false;
// check if there exist any node having value equal to (rootValue - root->data)
if (m.find(rootValue - root->data) != m.end())
return true;
// incrementing the current node's value
m[root->data]++;
// checking for left subtree
bool left = doesPairExist(root->left, m, rootValue);
// check for right subtree
bool right = doesPairExist(root->right, m, rootValue);
// decrementing the current node's value
m[root->data]--;
// if any of the subtrees consist of a pair then return the OR value
return left | right;
}
int main()
{
Tree *root = new Tree(9);
root->left = new Tree(5);
root->right = new Tree(7);
root->right->left = new Tree(9);
root->right->right = new Tree(12);
root->left->left = new Tree(4);
root->left->right = new Tree(8);
root->left->left->left = new Tree(10);
// to store the frequencies of values of every node
unordered_map<int, int> m;
// check if the left subtree or right subtree contains any pair in there root to leaf path
if (doesPairExist(root->left, m, root->data) | doesPairExist(root->right, m, root->data))
{
cout << "Yes" << endl;
}
else
{
cout << "No" << endl;
}
}
Output:
Yes
Complexity Analysis
Since we are performing the preorder traversal to find a pair, the time complexity would be O(N), where N would be the number of nodes present in the tree.
Since we are using extra space as an unordered map, we are storing the node's value in the map. Therefore the space complexity is O(N).
Check out this problem - Pair Sum In Array.




