Find if there is a Triplet in a Balanced BST that Adds to 0

Introduction

A triplet is a group of 3 members in a specific place. An example of this can be a set of three lines in a poem that rhyme. Similarly, in Binary Search Tree, a triplet is a group of three elements present in it. We will see this with an example also later.

This blog will discuss the problem of implementing Pair with a given sum in BST. We will discuss this article in detail.

Problem Statement

In this problem statement, we are given a Binary Search Tree (BST), and we have to find the triplet whose sum is ZERO.

Let's get a few examples to help us understand this problem statement.

Sample Examples

Example 1:    

Input : 

10,5,-15,1,12,11,13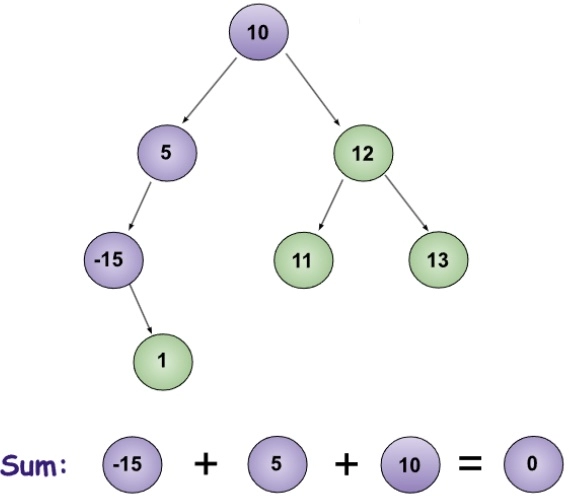

Output:

Triplet found: (-15 , 5 , 10)
 

Example 2:

Input: 

20,10,5,15,30,25,35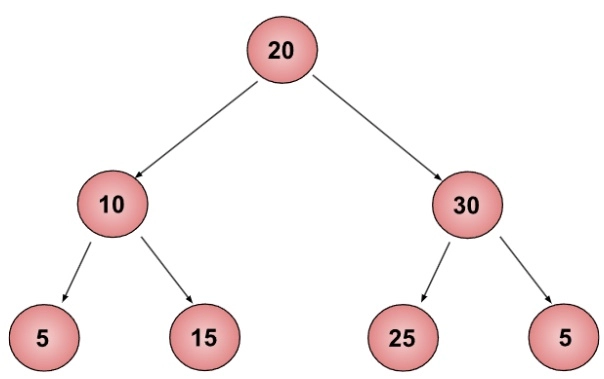

Output: 

Triplet not found

Approach 

The BST can be traversed easily by traversing through by Inorder and storing all of the nodes you encounter in an auxiliary array. Since Inorder traversal retrieves the nodes in increasing order of their values, this array would already be sorted. Check if a triplet is produced by an element in array A[i] and a pair from subarray A[i+1...n-1] for each element in array A[i].

Algorithm to find a triplet with a sum equal to zero in BST

1. Firstly, create a Doubly LinkedList (DLL) using the given BST.
    
2. Now, check the sum only for negative numbers while traversing the DLL.
    
3. We traverse DLL from head to tail for each negative number.
   
   
   • If the sum of data from the head and tail nodes is equal, the node will return true.
      
   • Move the head pointer to the next given node if it is less than the provided node.
      
   • Move the tail pointer to the previous node if it is greater than.
      
   • Repeat these steps until the head is not equal to the tail.

Implementation in Java

class Node
{
    int data;
    Node left, right;
    Node(int data)
    {
        this.data = data;
        this.left = this.right = null;
    }
}
class Tuple<X, Y, Z>
{
    public final X first;      
    public final Y second;  
    public final Z third;  
 
    private Tuple(X f, Y s, Z t)
    {
        this.first = f;
        this.second = s;
        this.third = t;
    }
 
    public static <X, Y, Z> Tuple <X, Y, Z> of(X a, Y b, Z c)
    {
        return new Tuple<>(a, b, c);
    }
}
 
class Nodes
{
    Node head, tail;
    Nodes() {}
}
 
class Main
{
    public static Node insert(Node root, int data)
    {
        if (root == null) {
            return new Node(data);
        }
 
        if (data < root.data) {
            root.left = insert(root.left, data);
        }
        else {
            root.right = insert(root.right, data);
        }
 
        return root;
    }
 
    public static void push(Node node, Nodes nodes)
    {
        node.right = nodes.head;
 
        if (nodes.head != null) {
            nodes.head.left = node;
        }
 
        if (nodes.tail == null) {
            nodes.tail = node;
        }
        nodes.head = node;
    }
 
    public static void conversion(Node root, Nodes nodes)
    {
        if (root == null) {
            return;
        }
 
        conversion(root.right, nodes);
 
        push(root, nodes);
 
        conversion(root.left, nodes);
    }
    public static Tuple<Integer, Integer, Integer> findTriplet(Node root, int target)
    {
        
        Nodes nodes = new Nodes();
        conversion(root, nodes);
        Node head = nodes.head;
        Node tail= nodes.tail;
        while (head!= null && head.right != tail)
        {
            
            Node start = head.right;
            Node end = tail;
 
            int pair_sum = target - head.data;
 
            while (start != end)
            {
                int curr_sum = start.data + end.data;
 
                if (curr_sum == pair_sum)
                {
                    return Tuple.of(head.data, start.data, end.data);
                }
                else if (curr_sum > pair_sum) {
                    end = end.left;
                }
                else {
                    start = start.right;
                }
            }
            head = head.right;
        }
 
        return null;
    }
 
    public static void main(String[] args)
    {
        int[] keys = { 10, -15, 3, -40, 20, 15, 50 };
 
        Node root = null;
        for (int key: keys) {
            root = insert(root, key);
        }
 
        int target = 20;
 
        Tuple<Integer, Integer, Integer> triplet = findTriplet(root, target);
 
        if (triplet != null)
        {
            System.out.println("Triplet found: (" + triplet.first + ", " +
                    triplet.second + ", " + triplet.third + ")");
        }
        else {
            System.out.println("Triplet not found");
        }
    }
}

Output: 

Triplet found: (-40, 10, 50)

Implementation in Java

#include <iostream> 
#include<queue> 
#include<map>
using namespace std;


struct node
{
    node* left;
    node* right; 
    int data;
};


node* newNode(int x)
{
    node* temp=new node();
    temp->left=NULL;
    temp->right=NULL;
    temp->data=x;
    return temp;
}


struct node* insert(struct node* node, int data)
{
    /* Return a new node; in case the tree is empty. */
    if (node == NULL) return newNode(data);
 
    /* Otherwise, recur down the tree */
    if (data <= node->data)
        node->left  = insert(node->left, data);
    else
        node->right = insert(node->right, data);
 
    /* return the (unchanged) node pointer */
    return node;
}


void conversion(node* root,node* &head,node* &tail) // we convet BST to DLL in INORDER fashion
{
 if(root==NULL)
     return;
  
 conversion(root->left,head,tail);  // recurse for the left subtree
 
 if(tail)           
     tail->right=root;   //assigning the next pointer for the previous node
 else                     
     head=root;           // Initially assigning the head pointer 
 
 root->left=tail;     //assigning the previous pointer for the current node
 tail=root;
 
 conversion(root->right,head,tail); // recurse for the right subtree
 
}


bool checkpairsum(int sum,node* head,node* tail)
{
    while(head!=tail) 
    {
        int x=head->data,y=tail->data;
        if(x+y==sum) 
        {   
         printf("Triplet found: (%d,%d,%d)",-1*sum,x,y);
            return true;
        }
        else if(x+y>sum)  
            tail=tail->left;
        else       //(x+y>sum)
            head=head->right; 
     //  printf("%d+%d!=%d \n",x,y,sum);
    }
    return false;
}


bool isTripletPresent(node* root)
{
    node* head=NULL,*tail=NULL;
    
    conversion(root,head,tail);  
    
    while(head->right!=tail && head->data<0)  
    {
        if(checkpairsum(-1*(head->data),head->right,tail))
            return true;
       
        head=head->right;
    } 
    return false;
}



int main()
{
    node* root = NULL;
    root = insert(root, 6);
    root = insert(root, -3);
    root = insert(root, 14);
    root = insert(root, -8);
    root = insert(root, 15);
    root = insert(root, 13);
    root = insert(root, 7);
    if (!(isTripletPresent(root)))
        printf("Triplet not found");
    return 0;
}

Output

Triplet not found

Time Complexity

The time complexity of the above approach for the problem of finding triplets in a BST whose sum is equal to zero is O(n²). Here, n is the number of elements in the Binary Search Tree. We have used nested loops that’s why the Time Complexity is in quadratic form. 
 

Space Complexity

The space complexity of the above approach for the problem of finding triplets in a BST whose sum is equal to zero is O(n). Here, n is the number of elements in the Binary Search Tree. 

Check out this problem - Pair Sum In Array.