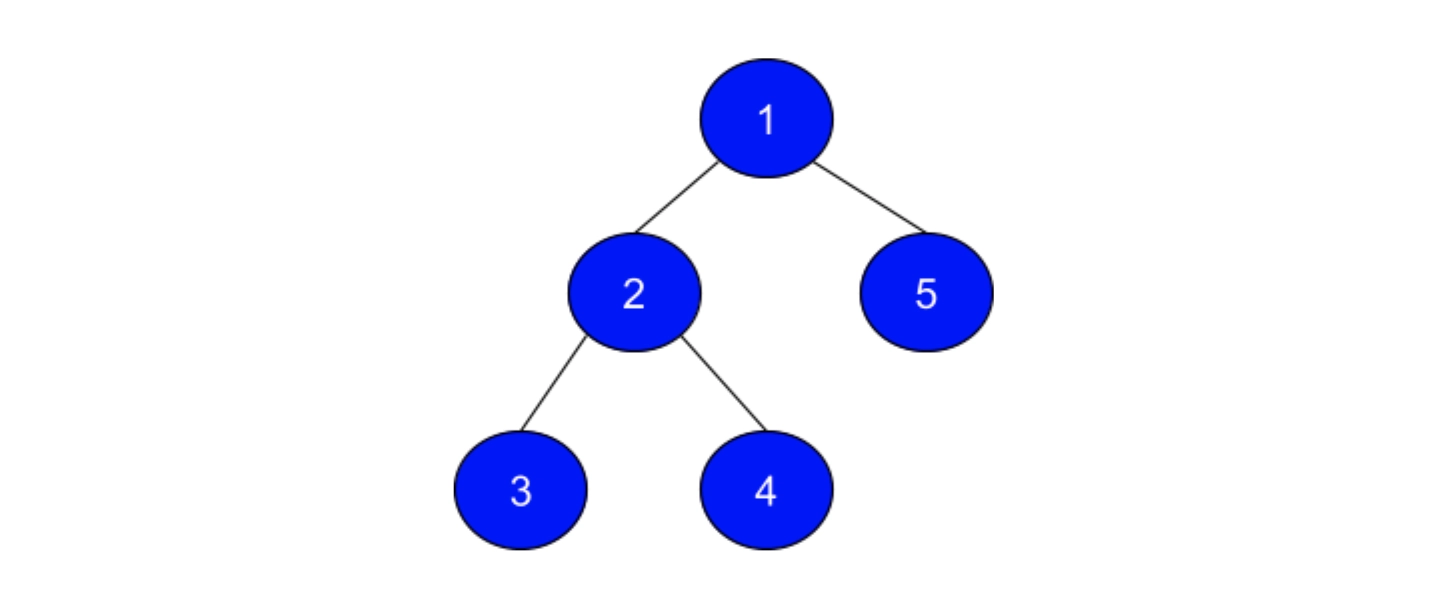
Intuition
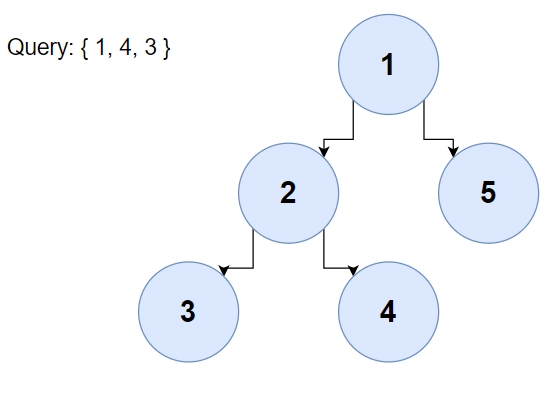
Let the query be {a, b, j}, where we have to find the 'j'th smallest node in the path between nodes' a' and 'b.' We can move from node 'b' towards node 'a' by making node 'a the tree's root for the current query and iterate from parent to parent.
Algorithm
Algorithm of the problem Find jth Smallest Value Present on the Simple Path between Two Nodes:
-
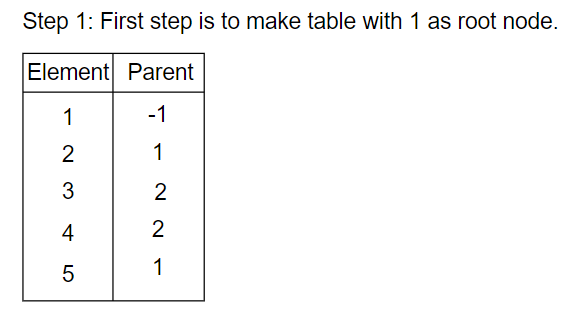
Function dfs() will be used to run Depth First Search(DFS Algorithm) and take a record of the parent of each node so that we can traverse from the node 'b' to node 'a iterating through the parents.
-
First, we will take the input 'N' and the number of queries' Q' followed by the vector 'P' to store the values of nodes. Then we will construct the graph by taking the input of edges. Then finally, we will start solving queries.
-
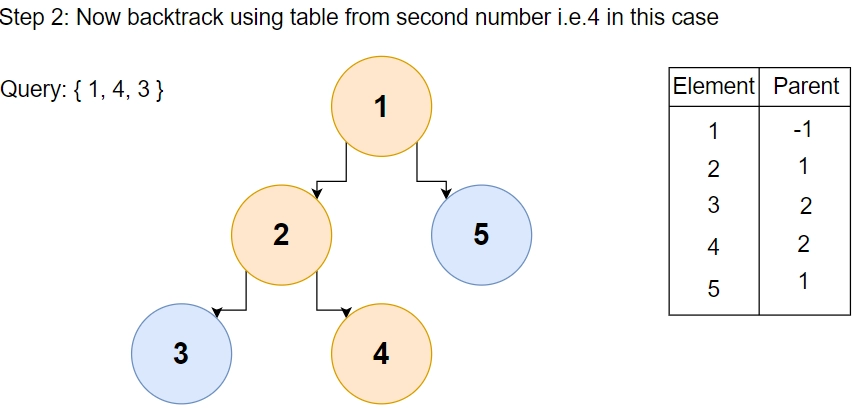
After taking the input of the query {a, b, j} in the primary function, we will call function "dfs()," making node 'a' as the root, so starting from node 'b,' we can easily reach node 'a' by moving one level up each time.
-
While moving one level up, we can store the values of the nodes in vector "pathNodes" and sort them to obtain 'j'th most minor node.
- If the total elements in "pathNodes" are less than 'j,' we will print -1; else, we will publish the answer.
Program
/*
C++ implementation of Find jth Smallest Value Present on the Simple Path between Two Nodes
*/
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void dfs(int node, int parent, vector<vector<int>>& edges, vector<int>& par)
{
par[node] = parent;
for (int &x : edges[node])
{
if (x == parent)
continue;
dfs(x, node, edges, par);
}
}
// Main function.
int main()
{
// Variables to store number of nodes and queries.
int n, q;
int x, y, a, b, j;
cin >> n >> q;
// Input of vector P.
vector<int> p(n + 1);
for (int i = 1; i <= n; i++)
cin >> p[i];
// Storing edges to generate graph.
vector<vector<int>> edges(n + 1, vector<int>(0));
for (int i = 1; i < n; i++)
{
cin >> x >> y;
edges[x].push_back(y);
edges[y].push_back(x);
}
// Vector to store parent of nodes.
vector<int> par(n + 1);
// Vector to store values of nodes on the path.
vector<int> pathNodes;
// Solving queries.
for (int i = 1; i <= q; i++)
{
// Input of query.
cin >> a >> b >> j;
// Clearing pathNodes.
pathNodes.clear();
// Running dfs considering node 'a' as the root.
dfs(a, -1, edges, par);
// Tracing path from node 'b' to node 'a'.
int tmp = b;
while (par[tmp] != -1)
{
// Storing values of nodes.
pathNodes.push_back(p[tmp]);
tmp = par[tmp];
}
pathNodes.push_back(tmp);
// Sorting to obtain the smallest element.
sort(pathNodes.begin(), pathNodes.end());
// Storing answer.
int ans = -1;
if (pathNodes.size() >= j)
ans = pathNodes[j - 1];
// Printing final answer.
cout << "query " << i << ": " << ans << endl;
}
return 0;
}
Input
5 2
1 2 2 4 3
1 2
1 5
2 3
2 4
1 3 2
2 5 1
Output
query 1: 2
query 2: 1
Complexity Analysis
Time complexity
The time complexity of “Find jth Smallest Value Present on the Simple Path between Two Nodes” is O(N x Q), where ‘N’ is the number of nodes and ‘Q’ is the number of queries.
Explanation: As we know, the time complexity of Depth First Search(DFS) on a tree with ‘N’ nodes is always O(N), and we are running such DFS for the ‘Q’ times. Thus the total complexity will be O(N x Q).
Space Complexity
The space complexity of “Find jth Smallest Value Present on the Simple Path between Two Nodes” is O(N x N), where ‘N’ is the number of nodes.
Explanation: The vector of vectors used to store edges of the tree occupies O(N x N), which is the most expensive occupancy of the space.
Frequently Asked Questions
What is a binary tree?
A binary tree is a tree data structure having a maximum of two children. There can only be two children per element in a binary tree; hence we usually refer to them as the left and right children.
What is a binary search tree?
A binary search tree is a binary tree in which all of the nodes left to the root node have values less than the root node, and all of the nodes right to the root node have values greater than the root node.
What is a Full Binary Tree?
A full binary tree is a particular kind of binary tree in which every parent node and internal node either has two children or none at all.
How do you tell whether two trees are the same?
If two binary trees contain the same data and arrangement, they are identical. By visiting both trees and comparing their data and arrangements, this can be accomplished.
What benefits does binary search offer?
Because the amount of data to be searched is reduced by half with each step in a binary search, one of its key benefits is that it is faster than a serial search.
Conclusion
The above blog has covered a critical interview question frequently asked in big MNCs where Data Structures and Algorithms play an essential role. ‘Find jth Smallest Value Present on the Simple Path between Two Nodes’ is a good problem related to undirected trees, which would help us understand graphs more deeply. Here are more similar problems like “Find jth Smallest Value Present on the Simple Path between Two Nodes”:
Find more such interesting questions on our practice platform Coding Ninjas Studio if you want to learn more before practicing, head over to our library section for many exciting blogs. Keep learning.
Happy Coding!
38+ registered 