Introduction
In this article, we will discuss a famous problem of the matrix. But before discussing the problem, let us first understand what is a row-wise sorted matrix, it is a matrix that is arranged in such a way that all the elements in a row are sorted in increasing order, and in a row 'i', where 1 <= i <= n-1, the first element of row 'i' is greater or equal to the last element of row '1'.
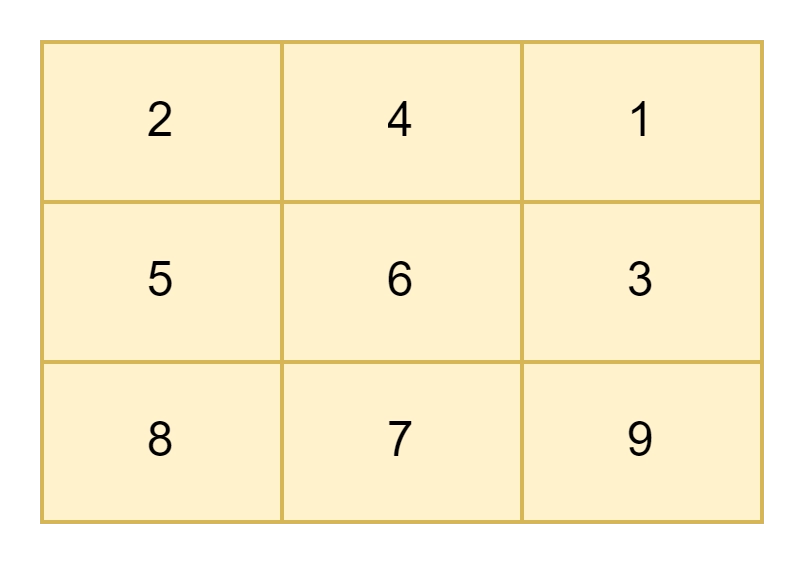
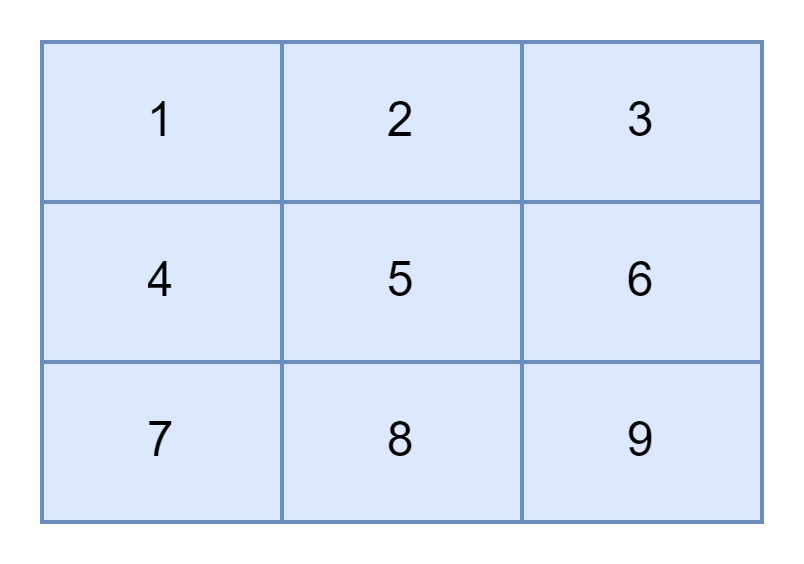
Unsorted matrix Sorted matrix
Problem statement
We are given a row-wise sorted matrix of size M, N where M and N represent rows and columns, respectively. Our task is to find the median of a matrix of the row-wise sorted matrix.
Examples
Input
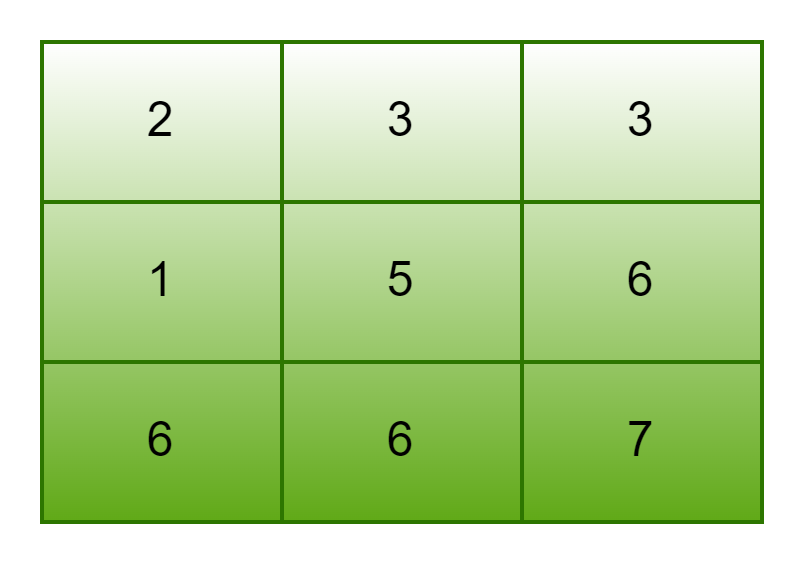
Output
The Median is 5.
Input

Output
The Median is 4.
Input

Output
The Median is 2.
In the above examples, we have found the median of a row-wise sorted matrix.
Recommended Topic, Array Implementation of Queue and Rabin Karp Algorithm
Brute force Approach
In the brute force approach, to find the median of a row-wise sorted matrix, just fill all the elements in an array and after that sort the array, now we just need to print the middle element of the array, in case of even size array the average of the two middle elements is considered.
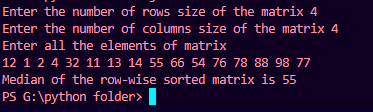
Implementation in Java
import java.util.*;
class median {
public static void main(String args[]) {
int row, col;
Scanner scan = new Scanner(System.in);
// entering the row, column and elements of matrix respectively.
System.out.print("Enter the number of rows in the matrix");
row = scan.nextInt();
System.out.print("Enter the number of columns in the matrix ");
col = scan.nextInt();
int [][]A=new int[row][col];
System.out.println("Enter all the elements of matrix");
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
A[i][j] = scan.nextInt();
}
}
// finding the median of the matrix
int[] median = new int[row * col];
int index = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
median[index] = A[i][j];
index++;
}
}
System.out.println("Median of the row-wise sorted matrix is"+ median[(row * col) / 2]);
}
}
Output

Complexity Analysis
Time complexity
As we all know the time complexity required to sort the n elements of an array is O(n*log(n)) so if we change the number of the elements from n to ( r1*c1) the time complexity would be O((r1*c1)*log(r1*c1)) for sorting the elements of the matrix and finding the median of the row-wise sorted matrix.
Space complexity
The space complexity would be O(row*col) for storing the elements in a linear array.