Problem
You are given a multigraph with no self-loops. Let us represent the graph by G(V, E) where V is the set of vertices and E is the multiset of edges.
Cut: A cut in this graph is defined as the partition of vertices into two non-empty sets (S, V-S). (Note: S != V and S != ɸ).
Weight of a cut: The weight of a cut is defined as the sum of weights of edges crossing the cut.
S-T cut: A S-T cut is a cut that divides the source and the sink into different subsets. The weight of an S-T cut is the total weight of edges going from the source’s set to the sink’s set.
Minimum S-T cut: A S-T cut having the minimum weight is called a minimum cut.
You have to find a minimum S-T cut of graph G. You have to divide the vertices into two non-empty sets, one containing source and another containing sink, such that the weight of cross edges is minimized.
Algorithm
Prerequisite: Ford-Fulkerson Algorithm
We use the Ford-Fulkerson algorithm to find maximum flow from source to sink in a graph. In the Ford-Fulkerson algorithm, we study that the maximum flow through a path equals the minimum capacity edge on that path.
For example, consider the following image.
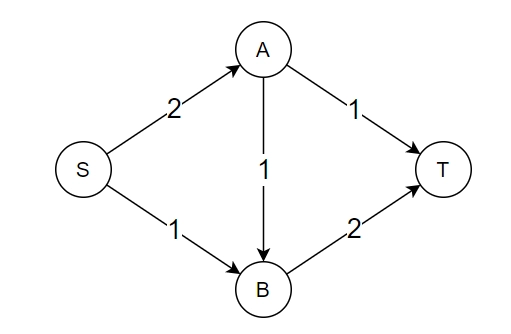
The maximum flow from S to T in the above image is 3.
Explanation:
- Choose the path S->A->T. The minimum capacity edge in this path is A-T having a capacity equal to 1. Therefore, a maximum 1 unit flow can pass through this edge. Now, we subtract this value from all the edges in this path. The capacity of S->A will become 1 and A->T will become 0.
- Choose the path S->A->B->T. The minimum capacity edge here is S->A and A->B, having capacity 1. Now we subtract this value from all the edges of this path.
- Now we can choose the path from S->B->T. Again, the maximum amount of flow that can pass through this edge equals 1.
Thus, from the Ford-Fulkerson algorithm, we can get the capacity of the minimum S-T cut. The thing left to do is find all the edges that form the minimum S-T cut. We can find the edges using the final residual graph of the Ford-Fulkerson algorithm.
Let V be the set of vertices that are reachable from the source in the residual graph. This means that these vertices belong to the same set as S. All the remaining vertices belong to the other set as T. Now the edges of the minimum S-T cut will be all the edges from the first set to the second set.
Implementation
#include <bits/stdc++.h>
using namespace std;
// Function to perform BFS
int bfs(vector<vector<int>>residualGraph, int s, int t, vector<int>&parent){
int n = residualGraph.size();
vector<int>vis(n, 0);
// Initialising queue and visited array
queue<int>q;
vis[s]=1;
parent[s]=-1;
q.push(s);
while(!q.empty()){
int u = q.front();
q.pop();
for(int v=0; v<n; v++){
// If node is not visited and capacity is greater than 0
if (!vis[v] && residualGraph[u][v]>0){
q.push(v);
parent[v]=u;
vis[v]=1;
}
}
}
// Will return 1 only if T was reachable from S
return (vis[t]==1);
}
// Function to perform DFS
void dfs(vector<vector<int>>residualGraph, int s, vector<int>&vis){
vis[s]=1;
int n = residualGraph.size();
for(int i=0; i<n; i++){
if (residualGraph[s][i] && vis[i]==0){
dfs(residualGraph, i, vis);
}
}
}
// Function to find minimum S-T cut of the given graph
void solve(vector<vector<int>>graph, int s, int t){
// Initialising residual graph
vector<vector<int>>residualGraph;
int n = graph.size();
for(int i=0; i<n; i++){
residualGraph.push_back(graph[i]);
}
vector<int>parent(n);
// Performing BFS till source and sink are reachable
while(bfs(residualGraph, s, t, parent)){
// Iterating over the path from sink to source
int cur_flow = INT_MAX;
for (int i=t; i!=s; i=parent[i]){
int j = parent[i];
// Updating the value of current flow through path
cur_flow = min(cur_flow, residualGraph[j][i]);
}
// Updating the residual graph
for(int i=t; i!=s; i=parent[i]){
int j = parent[i];
residualGraph[j][i] -= cur_flow;
residualGraph[i][j] += cur_flow;
}
}
// Till now we have got the weight of minimum S-T cut
vector<int>vis(n, 0);
// Performing DFS to see the vertices that are reachable from S
dfs(residualGraph, s, vis);
// Printing the edges if the minimum S-T cut
for (int i=0; i<n;i++){
for (int j=0; j<n; j++){
if (vis[i] && !vis[j] && graph[i][j]){
cout<<i<<" -> "<<j<<endl;
}
}
}
return;
}
// Driver code
int main(){
vector<vector<int>>graph;
int s=0, t=5;
graph.push_back({0, 10, 14, 4, 0, 0});
graph.push_back({0, 0, 8, 12, 0, 0});
graph.push_back({0, 6, 0, 0, 12, 0});
graph.push_back({0, 10, 6, 0, 0, 20});
graph.push_back({0, 8, 0, 6, 0, 4});
graph.push_back({0, 0, 0, 0, 0, 0});
solve(graph, s, t);
}Output
3 -> 5
4 -> 5Time Complexity
In the above implementation, to find the minimum S-T cut, we use BFS to find the path from S to T having the minimum number of edges. For every such path, we are finding the edge with minimum capacity in this path to find the maxflow from it. Since we use an adjacency matrix representation, BFS will take O(V^2) time, where V is the number of vertices.
We perform the BFS until T is not reachable from S. In every iteration, we pick one edge from the path and make its capacity 0. Therefore, the maximum number of times we perform BFS will be O(E), where E is the number of edges.
Therefore, the time complexity of the above approach is O(V^3 * E).
Space Complexity
We used an adjacency matrix representation of the graph, which will take O(V^2) space. Other than this, we created parent and visited arrays that will take O(V) space. Therefore, the total space complexity of the above approach is O(V^2).




