Solution
The objective is to use the shortest path algorithm. We first delete each edge from the graph one at a time before calculating the shortest distance between any two corner vertices. Before we process the next edge, we add an edge back.
Algorithm
Let’s discuss the algorithm steps.
Step1: Create an empty vector of size "E" ( E is the total number of edges). Each element of this vector holds information about every edge in the graph.
Step2: Traverse each edge[i] one at a time.
- Remove the 'edge[i]' from graph 'G' first.
- Get the current edge vertices that we just deleted from the graph.
- Using Dijkstra's shortest path algorithm, determine the shortest path between them.
- To create a cycle, we add the weight of the edge that was removed to the shortest path.
- If necessary, update min_weight_cycle.
Step3: Finally, return the minimum weighted cycle.
Code Implementation
C++
#include<bits/stdc++.h>
using namespace std;
# define INF 0x3f3f3f3f
// creating a struct for an edge
struct Edge
{
int u, v, wt;
};
class Graph
{
int V;
// adjacency list
list < pair <int, int > >*adjacency;
vector < Edge > edges;
public :
Graph( int V )
{
this->V = V ;
adjacency = new list < pair <int, int > >[V];
}
// declaring all the functions
// inserting an edge
void insertEdge ( int u, int v, int w );
// deleting an edge
void deleteEdge( int u, int v, int w );
// finding minimum path
int minimumPath (int u, int v );
// deleting an edge
void deleteEdge( int u, int v );
// finding min cycles
int FindMinCycle();
};
// inserting an edge
void Graph :: insertEdge ( int u, int v, int w )
{
adjacency[u].push_back( make_pair( v, w ));
adjacency[v].push_back( make_pair( u, w ));
Edge e = { u, v, w };
edges.push_back ( e );
}
// deleting an edge
void Graph :: deleteEdge( int u, int v, int w )
{
adjacency[u].remove(make_pair( v, w ));
adjacency[v].remove(make_pair(u, w ));
}
// finding minimum path function
int Graph :: minimumPath ( int u, int v )
{
// storing vertices
set< pair<int, int> > setds;
// vector for distances
vector<int> dist(V, INF);
/* insert self source at first and initialize its distance as 0 */
setds.insert(make_pair(0, u));
dist[u] = 0;
while (!setds.empty())
{
/* The first vertex in Set is the one with the shortest distance; remove it from Set. */
pair<int, int> tmp = *(setds.begin());
setds.erase(setds.begin());
/* To preserve the vertices sorted distance, vertex label must be put in second of pair (distance must be first item in pair) */
int u = tmp.second;
list< pair<int, int> >::iterator i;
for (i = adjacency[u].begin(); i != adjacency[u].end(); ++i)
{
int v = (*i).first;
int weight = (*i).second;
if (dist[v] > dist[u] + weight)
{
/* If the distance of v is not INF, then it must be in our set; therefore, it should be removed and reinserted with an updated shorter distance. We only remove from Set the vertices for which the distance has been determined. Therefore, they would never see us arrive here. */
if (dist[v] != INF)
setds.erase(setds.find(make_pair(dist[v], v)));
dist[v] = dist[u] + weight;
setds.insert(make_pair(dist[v], v));
}
}
}
return dist[v] ;
}
// finding minimum path function
int Graph :: FindMinCycle ( )
{
int min_cycle = INT_MAX;
int E = edges.size();
for ( int i = 0 ; i < E ; i++ )
{
Edge e = edges[i];
/* Obtain the edge vertices that we currently delete from the graph, and then use Dijkstra's shortest path technique to discover the shortest path between these two vertices. */
deleteEdge( e.u, e.v, e.wt ) ;
int dist = minimumPath( e.u, e.v );
/* If this is the shortest cycle, update min cycle; otherwise, add weight to currently deleted edges to create a cycle. */
min_cycle = min(min_cycle, dist + e.wt);
// add current edge back to the graph
insertEdge( e.u, e.v, e.wt );
}
return min_cycle ;
}
int main()
{
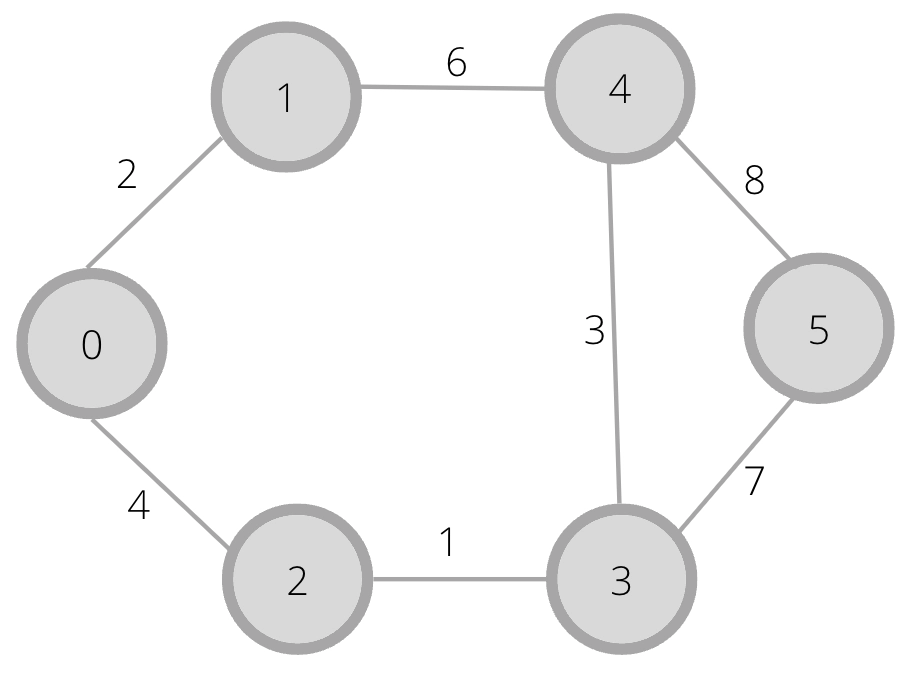
int V = 6;
Graph g(V);
g.insertEdge(0,1,2);
g.insertEdge(0,2,4);
g.insertEdge(1,4,6);
g.insertEdge(2,3,1);
g.insertEdge(3,4,3);
g.insertEdge(3,5,7);
g.insertEdge(4,5,8);
cout << "Minimum weight cycle in the graph is: "<<g.FindMinCycle() << endl;
return 0;
}

You can also try this code with Online C++ Compiler
Output
Minimum weight cycle in the graph is 16.
Python
# Minimum weight cycle in an undirected graph
from sys import maxsize
INF = int(0x3f3f3f3f)
class Edge:
def __init__(self, u: int,v: int,wt: int) -> None:
self.u = u
self.v = v
self.wt = wt
class Graph:
def __init__(self, V: int) -> None:
self.V = V
self.adjacency = [[] for _ in range(V)]
self.edge = []
# inserting an edge
def addEdge(self, u: int, v: int, w: int) -> None:
self.adjacency[u].append((v, w))
self.adjacency[v].append((u, w))
e = Edge(u, v, w)
self.edge.append(e)
#removing an edge
def removeEdge(self, u: int, v: int, w: int) -> None:
self.adjacency[u].remove((v, w))
self.adjacency[v].remove((u, w))
# finding minimum path
def minimumPath(self, u: int, v: int) -> int:
"""The first vertex in Set is the one with the shortest distance; remove it from Set."""
setds = set()
dist = [INF] * self.V
setds.add((0, u))
dist[u] = 0
while (setds):
tmp = setds.pop()
"""To preserve the vertices sorted distance, vertex label must be put in second of pair (distance must be first item in pair)"""
uu = tmp[1]
for i in self.adjacency[uu]:
vv = i[0]
wt = i[1]
if (dist[vv] > dist[uu] + wt):
"""If the distance of v is not INF, then it must be in our set; therefore, it should be removed and reinserted with an updated shorter distance. We only remove from Set the vertices for which the distance has been determined. Therefore, they would never see us arrive here."""
if (dist[vv] != INF):
if ((dist[vv], vv) in setds):
setds.remove((dist[vv], vv))
dist[vv] = dist[uu] + wt
setds.add((dist[vv], vv))
return dist[v]
# finding minimum cycle
def FindMinCycle(self) -> int:
min_cycle = maxsize
E = len(self.edge)
for i in range(E):
e = self.edge[i]
"""Obtain the edge vertices that we currently delete from the graph, and then use Dijkstra's shortest path technique to discover the shortest path between these two vertices."""
self.removeEdge(e.u, e.v, e.wt)
distance = self.minimumPath(e.u, e.v)
"""If this is the shortest cycle, update min cycle; otherwise, add weight to currently deleted edges to create a cycle."""
min_cycle = min(min_cycle,distance + e.wt)
# adding current edge back to the graph
self.addEdge(e.u, e.v, e.wt)
return min_cycle
# Main Code
if __name__ == "__main__":
V = 6
g = Graph(V)
g.addEdge(0,1,2)
g.addEdge(0,2,4)
g.addEdge(1,4,6)
g.addEdge(2,3,1)
g.addEdge(3,4,3)
g.addEdge(3,5,7)
g.addEdge(4,5,8)
print("Minimum weight cycle in the graph is: ",g.FindMinCycle())

You can also try this code with Online Python Compiler
Output
Minimum weight cycle in the graph is 16.
Time and Space Complexity
Time Complexity: O( E *(E * log V)), For every edge, we run Dijkstra’s shortest path algorithm so overall time complexity E^2*(logV). Where E is the number of edges and V is the number of vertices in the graph.
Space Complexity: O(V+E) where V denotes the number of vertices and E is the number of edges in the graph.
Check out this problem - Pair Sum In Array.
Frequently Asked Questions
What is a Graph?
A graph is a non-linear data structure made up of nodes and edges. In a graph, the edges are the lines or arcs that link any two nodes, and the nodes are occasionally referred to as vertices.
What is an Undirected Graph?
Undirected graphs have edges that do not have a direction. Each edge may be traversed in both directions, which indicates a two-way connection.
What is a Directed Graph?
A directed graph is one where all the edges are directed from one vertex to another. There is only a one-way connection between vertices.
What is Dijkstra Algorithm?
Dijkstra's algorithm is used to find the shortest path between any two vertices of a graph.
What is a weighted graph?
A weighted graph is one in which the edges are labelled with numbers (called weights).
Conclusion
In this article, we have extensively discussed how to find the minimum weight cycle in an undirected graph, its algorithm, space and time complexity, and implementation in different programming languages.
If you want to learn more, check out our articles on Construct the Full K-ary Tree from its Preorder Traversal, Detect cycle in an undirected graph, Regular and Bipartite graphs, and Planar and Non-Planar Graphs.
Happy Coding!