Brute Force Approach
By using DFS traversal on each component, the problem can be easily and quickly solved. A component is visited every time the DFS() function is called. The DFS function will call the next unvisited component. The number of connected components is determined by how many times DFS() function is called. This question can also be solved using Breadth-First Search(BFS).
A cell in a 2D matrix has 8 neighbors altogether. In the standard DFS technique, we recursively call all the adjacent vertices. But in this case, we can recursively call for only eight neighbors. To prevent further visits, we keep track of the visited 1s.
Algorithm
-
We will keep track of visited vertices of the graph by creating a matrix named visited_nodes, which stores boolean values for every cell, whether it is visited or not.
-
We will make a function that will check whether a particular cell (given the row and column) is in range. Let’s name the function valid_node().
-
Another function, dfs (), is created for performing a Depth-First search on a particular node that takes node and graph as its parameters. It only treats the eight nearby vertices as neighboring vertices.
-
Inside the dfs() function, Mark the particular cell as visited(i.e., visited[i][j]=True) and perform DFS on all its neighbors.
-
The primary function number_of_Islands() in a given boolean 2D matrix that returns the number of islands in that undirected graph is created.
-
Initialize a variable named number_of_islands with value 0 and traverse through the entire graph matrix.
-
A new island is discovered if a cell with the value 1 has yet to be visited. To increase the island count, visit every cell on this island.
Python Implementation
class Solution:
def __init__(self):
self.visited_nodes = []
#function to check whether the cell is in range or not
def valid_node(self, x, y, graph):
x_range = 0<=x and x<len(graph)
y_range = 0<=y and y<len(graph[0])
return x_range and y_range
#function to perform the depth-first search
#on every unvisited node
def dfs(self, node, graph):
#mark the particular node to be visited
self.visited_nodes[node[0]][node[1]] = True
movements = [[-1, 0], [1, 0], [0, 1], [0, -1],
[1, 1], [1, -1], [-1, 1], [-1, -1]]
for m in movements:
i = node[0] + m[0]
j = node[1] + m[1]
#performing the depth-first search on nodes that are not visited yet
#and the cell is in range
valid = self.valid_node(i,j,graph)
if valid and graph[i][j]==1 and not self.visited_nodes[i][j]:
self.dfs([i, j], graph)
#function to return the number of islands
#found in the given 2D boolean matrix
def number_of_Islands(self,graph):
ones = []
for i in range(len(graph)):
self.visited_nodes.append([])
for j in range(len(graph[i])):
if graph[i][j] == 1:
ones.append([i, j])
self.visited_nodes[i].append(False)
#variable to count the number of islands
number_of_islands = 0
for node in ones:
if not self.visited_nodes[node[0]][node[1]]:
self.dfs(node,graph)
number_of_islands +=1
return number_of_islands
graph =[[1, 1, 1, 0, 0],
[0, 0, 0, 0, 1],
[1, 0, 1, 1, 1],
[0, 0, 0, 0, 0],
[1, 0, 1, 0, 1]]
#making the object of Solution class
obj=Solution()
answer = obj.number_of_Islands(graph)
#printing the answer
print("Total number of islands is"+" "+str(answer))

You can also try this code with Online Python Compiler
Output:
Total number of islands is 6
Explanation: Clearly, we can see the 6 islands in this graph.

Complexity Analysis
Time Complexity: O(n*m), where n is the number of rows and m is the number of columns in an undirected graph's input boolean 2D matrix.
Reason: We are simply traversing the entire boolean matrix of size n*m and checking whether it is visited or not. So, traversing takes a complexity of O(n*m)
Auxiliary Space Complexity: O(n*m)
Reason: This algorithm required a matrix named visited of size n*m, which implies that this method occupies a space of n*m, making the space complexity as O(n*m)
Optimized Approach
The above method can further be optimized without using extra space, i.e., without using the visited matrix. Altogether the approach is almost the same as the earlier one. The only difference is we are changing the input 2D boolean matrix itself to mark a particular cell as visited (i.e., g[i][j]==-1) rather than using the extra space of equal size as the matrix and using that matrix to track the visited cells. We traverse the complete matrix and recursively perform Breadth-First Search on all 8 neighbors of a node and keep finding an island.
Algorithm
-
We traverse the given matrix for each row and column, and if the island is not visited, then we run a breadth-first search algorithm on all 8 neighbors.
-
We check for each neighbor separately if the neighbor is not visited, then enqueue the node in the queue and run a while loop to traverse the nodes in a BFS manner.
- Once all the neighbors are considered, and no new connected node is left. We remove the current node from the queue.
-
We count the number of times the BFS loop is called, giving us the required value, i.e., the number of islands.
- Return the number of islands to the main function and print the value.]
Let us understand the algorithm by performing a dry run on an example.
Example input
graph = [ [1, 1, 1, 0, 0],
[0, 0, 0, 0, 1],
[1, 0, 1, 1, 1],
[0, 0, 0, 0, 0],
[1, 0, 1, 0, 1] ]
We begin with index (0,0) and find an island (i.e., 1). So, we check for the neighbors of (0,0) and add those that have the value 1 to the queue(here (0,1)) and mark (0,0) as visited.

Now we check for the neighbors of (0,1) and add (0,2) to the queue. We ignore (0,0) because it is already visited.

Next, when we check for (0,2) we find no unvisited neighbor nodes with value 1. The node (0,1) is ignored because it is already visited.
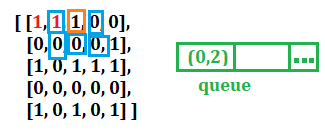
So we find our first island and increment the numOfIslands by 1.

Similarly, we continue until we find another node with value 1 and repeat the whole process until we reach the bottom right element of the graph. We conclude that we have 6 islands in total in our example.

Hence, output 6.
C++ Implementation
#include <iostream>
using namespace std;
#include<vector>
#include<queue>
/* This function will count the number of islands */
int numberOfIslands(vector<vector<int>> & grid, int n, int m){
/* Queue is used to keep track of the connected parts of the graph */
queue<pair<int, int>> q;
pair<int, int> p;
int x, y, numOfIslands= 0;
/* For each row */
for(int i =0; i<n; i++){
/* For each column */
for(int j=0; j<m; j++){
/* If the value is 1 then it is an island that is not visited yet*/
if(grid[i][j] == 1){
/* Add the cell to the queue */
q.push(make_pair(i,j));
/* -1 indicates that the island is visited */
grid[i][j] =-1;
/* Loop until all nodes are visited */
while(! q.empty()){
p = q.front();
// x will contain the row value and y will contain the column value
x = p.first;
y = p.second;
//up cell
if(x-1 >= 0){
if(grid[x-1][y] == 1){
q.push(make_pair(x-1, y));
grid[x-1][y] == -1;
}
}
//down cell
if(x+1 <= n-1){
if(grid[x+1][y] == 1){
q.push(make_pair(x+1, y));
grid[x+1][y] = -1;
}
}
//left cell
if(y-1 >= 0){
if (grid[x][y-1] == 1){
q.push(make_pair(x, y-1));
grid[x][y-1] = -1;
}
}
//right
if(y+1 <= m-1){
if (grid[x][y+1] == 1){
q.push(make_pair(x, y+1));
grid[x][y+1] = -1;
}
}
//top right
if(x-1 >= 0 && y+1 <= m-1){
if (grid[x-1][y+1] == 1){
q.push(make_pair(x-1, y+1));
grid[x-1][y+1] = -1;
}
}
//top left
if(x-1 >= 0 && y-1 >= 0){
if (grid[x-1][y-1] == 1){
q.push(make_pair(x-1, y-1));
grid[x-1][y-1] = -1;
}
}
//bottom right
if(x+1 <= n-1 && y+1 <= m-1){
if (grid[x+1][y+1] == 1){
q.push(make_pair(x+1, y+1));
grid[x+1][y+1] = -1;
}
}
//top left
if(x+1 <= n-1 && y-1 >= 0){
if (grid[x+1][y-1] == 1){
q.push(make_pair(x+1, y-1));
grid[x+1][y-1] = -1;
}
}
/* Remove the current cell from the queue */
q.pop();
}
numOfIslands ++;
}
}
}
return numOfIslands;
}
/* Driver Function */
int main()
{
vector<vector<int>> graph;
graph = {{1, 1, 1, 0, 0},
{0, 0, 0, 0, 1},
{1, 0, 1, 1, 1},
{0, 0, 0, 0, 0},
{1, 0, 1, 0, 1}};
cout<<"Total number of islands is "<<numberOfIslands(graph, graph.size(), graph[0].size());
return 0;
}

You can also try this code with Online C++ Compiler
Python Implementation
def numberOfIslands(grid, n, m):
'''Queue is used to keep track of the connected parts of the graph'''
q = []
numOfIslands= 0
'''For each row '''
for i in range(n):
'''For each column'''
for j in range(m):
'''If the value is 1 then it is an island that is not visited yet'''
if grid[i][j] == 1:
'''Add the cell to the queue '''
q.append([i,j])
'''-1 indicates that the island is visited'''
grid[i][j] = -1
'''Loop until all nodes are visited'''
while(len(q) != 0):
p = q[0]
'''x will contain the row value and y will contain the column value'''
x = p[0]
y = p[1]
'''up cell'''
if x-1 >= 0:
if grid[x-1][y] == 1:
q.append([x-1, y])
grid[x-1][y] == -1
'''down cell'''
if x+1 <= n-1:
if grid[x+1][y] == 1:
q.append([x+1, y])
grid[x+1][y] = -1
'''left cell'''
if y-1 >= 0:
if grid[x][y-1] == 1:
q.append([x, y-1])
grid[x][y-1] = -1
'''right'''
if y+1 <= m-1:
if grid[x][y+1] == 1:
q.append([x, y+1])
grid[x][y+1] = -1
'''top right'''
if x-1 >= 0 and y+1 <= m-1:
if grid[x-1][y+1] == 1:
q.append([x-1, y+1])
grid[x-1][y+1] = -1
'''top left'''
if x-1 >= 0 and y-1 >= 0:
if grid[x-1][y-1] == 1:
q.append([x-1, y-1])
grid[x-1][y-1] = -1
'''bottom right'''
if x+1 <= n-1 and y+1 <= m-1:
if grid[x+1][y+1] == 1:
q.append([x+1, y+1])
grid[x+1][y+1] = -1
'''top left'''
if x+1 <= n-1 and y-1 >= 0:
if grid[x+1][y-1] == 1:
q.append([x+1, y-1])
grid[x+1][y-1] = -1
'''Remove the current cell from the queue '''
q.pop(0)
numOfIslands += 1
return numOfIslands
'''Driver Function '''
def main():
graph = [[1, 1, 1, 0, 0],
[0, 0, 0, 0, 1],
[1, 0, 1, 1, 1],
[0, 0, 0, 0, 0],
[1, 0, 1, 0, 1]]
print("Total number of islands is ", numberOfIslands(graph, len(graph), len(graph[0])))
return 0
'''Executing Main'''
main()

You can also try this code with Online Python Compiler
Output:
Total number of islands is 6
Complexity Analysis
Time Complexity: O(n*m), where n is the number of rows and m is the number of columns in the input boolean 2D matrix of an undirected graph.
Reason: This method also traversed the complete boolean matrix for counting the number of islands. So, time complexity remains the same as O(n*m)
Auxiliary Space Complexity: O(n*m)
Reason: BFS uses a queue structure to store the order of traversal. Hence a maximum of n*m space is required at a time for this purpose. We are not using a visited matrix, so that space is now saved.
Frequently Asked Questions
What is meant by an undirected graph?
An undirected graph is a collection of connected objects (also known as vertices or nodes) where all edges are two-way.
How do you find the number of connected components on a graph?
Mark each vertex as unvisited to start. Repeat after each vertex. DFS should be used on any unvisited vertex to increase the count by one. The value of count will represent the number of connected elements in the graph following iteration over all vertices.
How does DFS work?
When a search runs into a dead end during any iteration, the Depth First Search (DFS) algorithm employs a stack to keep track of where to go next to continue the search.
How does BFS work?
BFS stands for Breadth-first search. It is a traversal algorithm for graphs where the traversal is done level by level. We traverse the nodes at the k level before moving to those at the k+1 level.
What is a graph?
A graph is a non-linear data structure used to represent highly correlated data. It consists of vertices and edges. The vertices represent the nodes or elements of the graph, and the edges represent the relationships or connections between the nodes.
Conclusion
This article discussed the problem of finding the number of islands. We have discussed the brute force solution where, we used DFS Algorithm and an additional visited matrix to solve the problem. We then discussed the optimized approach using BFS.
We hope this blog helped you readily understand this problem and enhanced your knowledge about Depth-First Search and Breadth-First-Search used in Graphs.
Recommended Readings:
Refer to our guided paths on Coding Ninjas Studio, a platform we provide, Coding Ninjas. You can upskill yourself in Data Structure Algorithms, System Design, Basics of Machine Learning, and many more topics.
If you find our blogs informative and exciting, please vote for them.
Happy Coding and Learning!