Introduction
If you want to be good in competitive programming or in DSA. Then you need to have knowledge of various programming questions. In this blog, we will discuss a programming question related to the matrix or 2d array where we have to find the sum of all the elements in the matrix except some elements which will be given by the user and then print the result.
Also Read, Array Implementation of Queue and Rabin Karp Algorithm
Problem Statement
We have a two-dimensional matrix and a set of cell indexes. Cell indices are written as (i, j), where i is row and j is column. For any given cell index (i, j), we must calculate the sums of all matrix elements that do not appear in the ith row or jth column.
Sample Examples
Example 1
Input
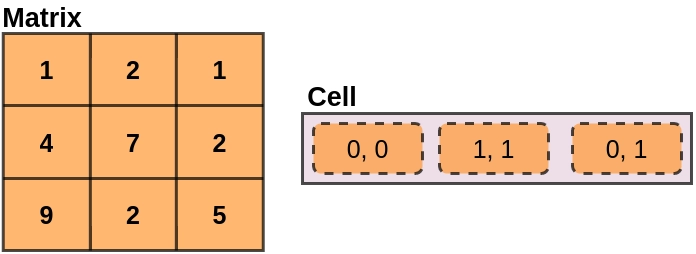
Output

Explanation
Excluding the 0th row and 0th column, we get 16 as our answer. The same goes for other cell indices.
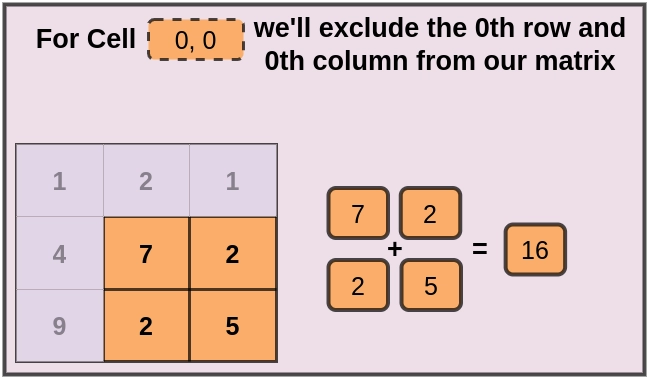
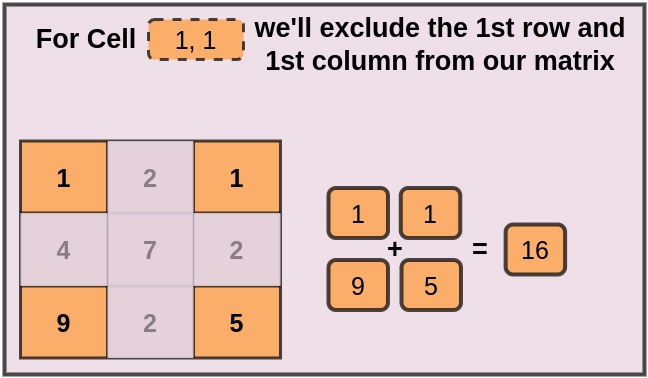
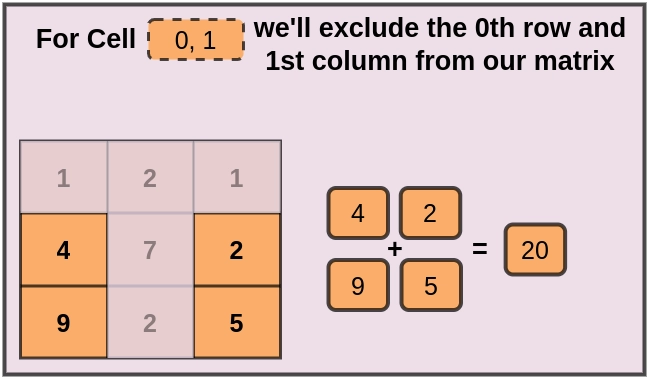
Example 2
Input
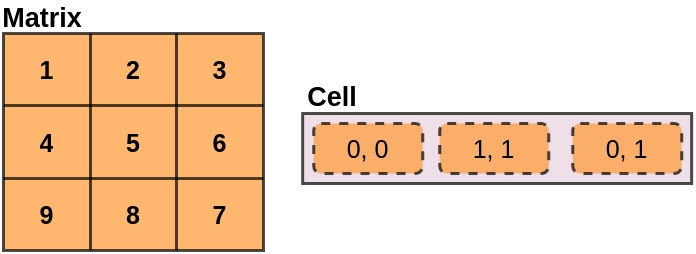
Output
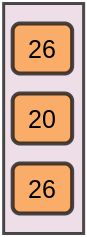
Explanation
Excluding the 0th row and 0th column, we get 26 as our answer. The same goes for other cell indices.
Brute Force Approach
Consider all cell indexes. Find the sum of matrix elements that are not present in either the i'th row or the j'th column for each cell index (i, j).
Algorithm
-
Start Traversing the matrix.
-
If the ith row and jth column is available in our Cell indexes. Then skip that iteration.
-
Else add the summation to a variable.
-
Print the sum.
-
Exit
Implementation in C++
#include<bits/stdc++.h>
using namespace std;
void findSum(vector<vector<int>> mat, pair<int, int> *cell, int n) {
// row size
int ROW = mat.size();
//column size;
int COL = mat[0].size();
// Iterating through whole matrix
for (int i=0; i<n; i++)
{
// saving result and getting the ith row and jth column
int result = 0, r = cell[i].first, c = cell[i].second;
// Computing the sum for current cell index
for (int j=0; j<ROW; j++)
for (int k=0; k<COL; k++)
if (j != r && k != c)
result += mat[j][k];
// printing the result
cout << result << endl;
}
}
// Driver program to test above
int main()
{
// getting row size from user
cout << "Enter Row Size: ";
int rowSize;
cin >> rowSize;
// getting column size from user
cout << "Enter Column Size: ";
int colSize;
cin >> colSize;
// main matrix
vector<vector<int>> mat(rowSize, vector<int>(colSize));
// getting matrix element from user
for(int i = 0; i < rowSize; i++){
for(int j = 0; j < colSize; j++){
cin >> mat[i][j];
}
}
// Size of our cell array
int n = 3;
// cell indexes that needs to be skipped
pair<int, int> cell[] = {{0, 0}, {1, 1}, {0, 1}};
// Calling our method
findSum(mat, cell, n);
return 0;
}
Input
Enter Row Size: 3
Enter Column Size: 3
1 2 3
4 5 6
9 8 7
Output
26
20
26Time Complexity
The Time Complexity of the above program is O(n * rowSize * colSize), where n represent the size of our cell indexes that needs to be skipped and rowSize, colSize represents the size of our matrix.
Space Complexity
No extra space is used so the space complexity will be O(1).
Read More - Time Complexity of Sorting Algorithms




