Introduction
Finding the sum of all left leaves in a given binary tree is a binary tree problem. It is a type of question that check the critical thinking and aptitude of the candidate. It also checks his grasp on the concept of binary trees and how well versed the candidate is in this concept.
In order to find the sum of all left leaves in a given binary tree, we will be using three approaches, the first will be a pre-order traversing, the second will be Breadth-first traversal and the last would be Depth-first traversal.
Problem Statement
We need to calculate the total number of leaf nodes in a binary tree. Each node in the binary tree must be traversed in order to determine whether the current node is a left-leaf node or not.
A node is a left leaf node if both the left and right child pointers of the current node are NULL and the current node is the left child of its parent.
Sample Examples
Example 1

Output

Explanation
We are traversing the whole tree, and we are finding the left leaf nodes present in the binary tree. Here only the node ‘7’ is present in the binary tree as the left leaf node. Then we’ll return that.
Example 2
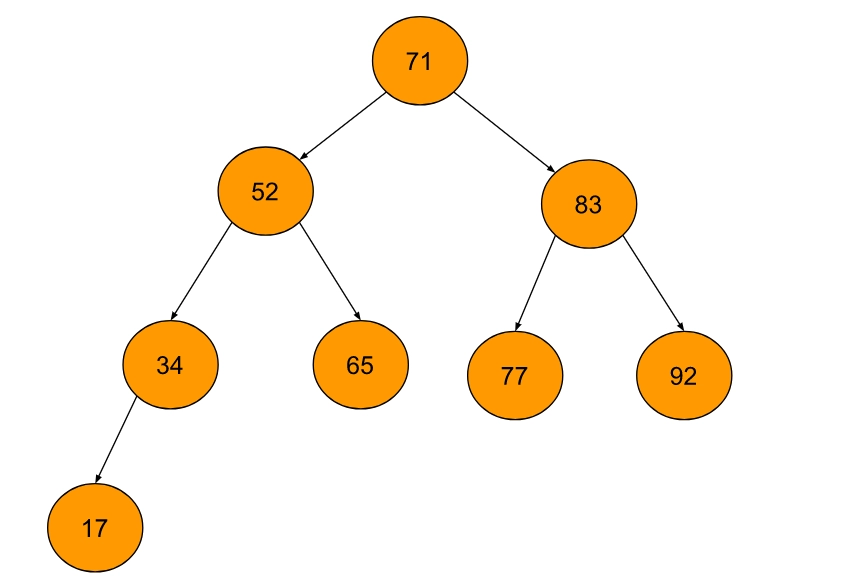
Output

Explanation
We are traversing the whole tree, and we are finding the left leaf nodes present in the binary tree. Here the nodes ‘17’ and ‘77’ are present as the left leaf nodes of the binary tree. Then we’ll return that.Approach 1(Pre-order traversing)
In this approach, we’ll traverse the tree in a pre-order fashion. Afterward, we’ll sum all the left leaves nodes that we found in the process.
Algorithm
- Pre-order traverse the binary tree that has been given.
-
A left leaf node should be present, so verify that. A binary tree node is a leaf node if and only if:
- if the current node is the parent's left child.
- if the current node's left and right child pointers are NULL.
- Add its value to the variable sum if the current node is a leaf node on the left.
- Recursively calculate the sum of the left leaf nodes in the left and right subtrees and return if the current node is not a left leaf node.
Implementation
#include <stdio.h>
#include <bits/stdc++.h>
#include <limits.h>
using namespace std;
struct node
{
int data;
struct node *left;
struct node *right;
};
struct node* getNewNode(int data)
{
/* dynamically allocate memory for a new node */
struct node* newNode = (struct node*)malloc(sizeof(struct node));
/* populate data in new Node */
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
struct node* generateBTree()
{
// Root Node
struct node* root = getNewNode(1);
root->left = getNewNode(2);
root->right = getNewNode(3);
root->left->left = getNewNode(4);
root->left->right = getNewNode(5);
root->right->right = getNewNode(6);
root->left->left->left = getNewNode(7);
root->left->left->right = getNewNode(8);
return root;
}
int isLeafNode(struct node *nodePtr)
{
if(nodePtr == NULL)
return 0;
else if (nodePtr->left == NULL && nodePtr->right == NULL)
return 1;
else
return 0;
}
/* This function calculates sum of all left leaf nodes in a binary tree */
int getleftLeafsSum(struct node *root)
{
int sum = 0;
if (root != NULL)
{
/*Check if left node of root is a leaf node */
if (isLeafNode(root->left))
{
/* Add left leaf node data to sum */
sum += root->left->data;
}
else
{
/* Recursively find sum of all left leaf nodes in left sub tree */
sum += getleftLeafsSum(root->left);
}
/* Recursively find sum of all left leaf nodes in left sub tree */
sum += getleftLeafsSum(root->right);
}
/* Now we’ll return sum of all left leaf nodes in a tree whose root node is root */
return sum;
}
int main() {
struct node *root = generateBTree();
cout<<"Left Leaf Sum : "<< getleftLeafsSum(root);
return 0;
}
Output

Time Complexity
Pre-order traversing is used to traverse through the binary tree, that’s why the time complexity of the approach is O(n).
Space Complexity
Pre-order traversing is used to traverse through the binary tree, and we know that pre-order traversing takes O(n), auxiliary space, so the space complexity of the approach is O(n).
Also check out - Inorder Predecessor





