Algorithm
Let us discuss the algorithm to be followed for the given problem statement:
-
We will use a recursive approach to solve the given problem.
-
First, we begin our search for the ‘N’ element at the root node.
-
If we reach a leaf node with a value greater than ‘N’, the ‘N’ element does not exist, and we return -1.
-
Otherwise, if the node value is less than or equal to ‘N’ and the right subtree value is NULL or greater than ‘N’, we will return the node value as the output.
- If the value of the root node is greater than ‘N’, search for the element in the left subtree; otherwise, search for the ‘N’ element in the right subtree by calling the same function and passing the left or right values appropriately.
Dry Run
Let's now discuss working through an example, and then we will code it:
We will be taking the same BST as above.
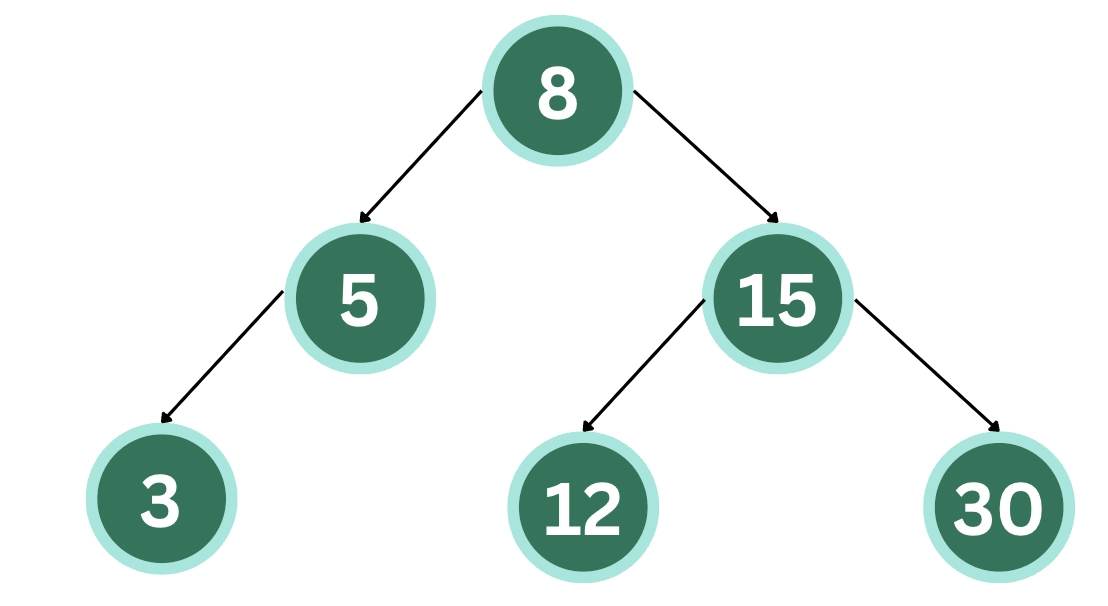
We will be taking the N as 13. Then we will be checking if the root node is less than or equal to N.
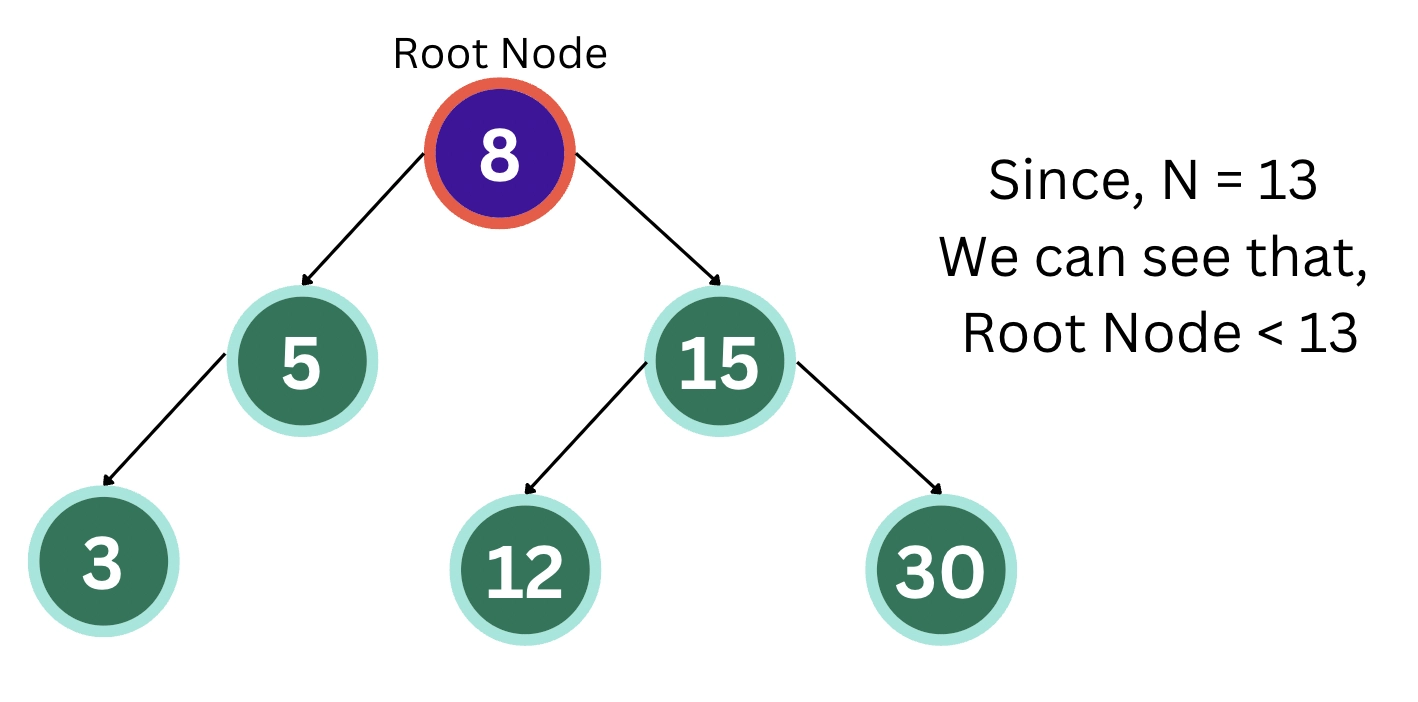
Since the root node is less than 13, we will move ahead with searching in the right subtree.
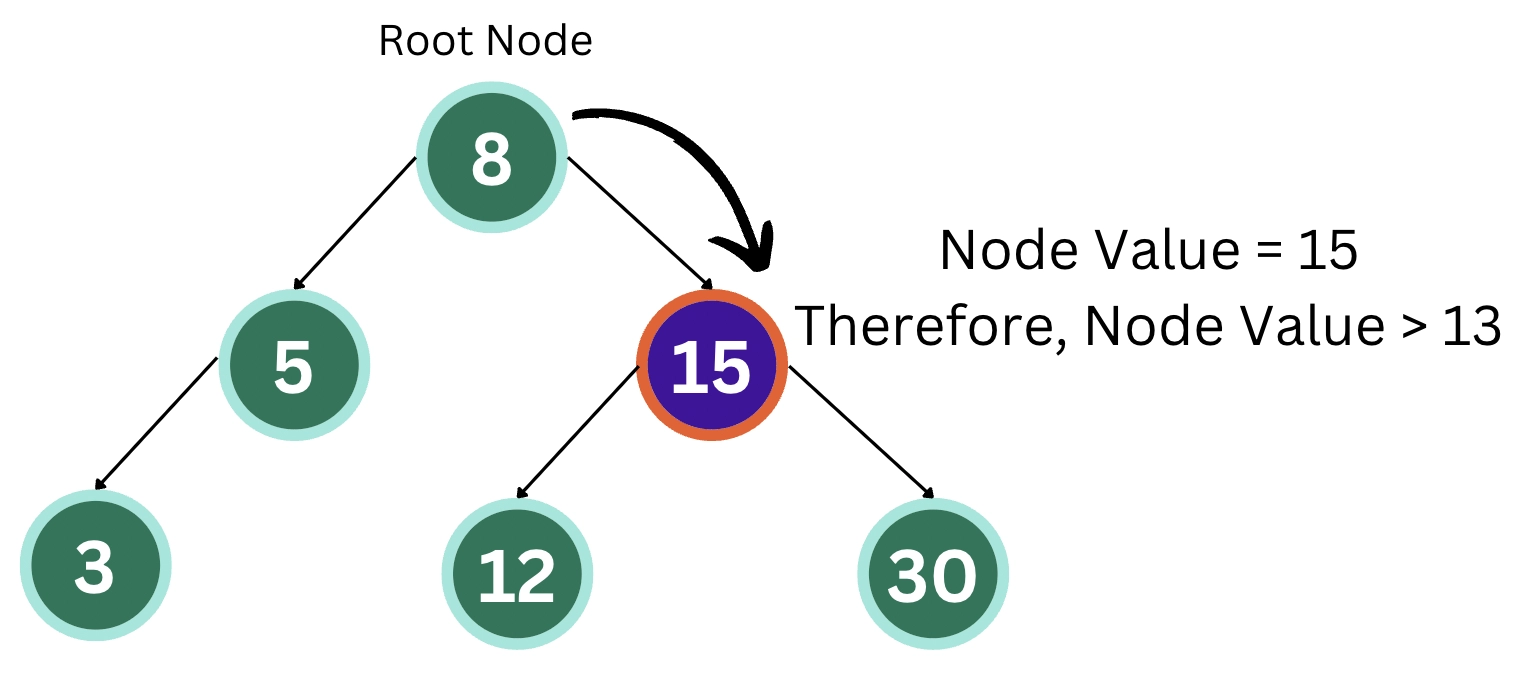
We will now move ahead with searching in the left subtree of node value 15.
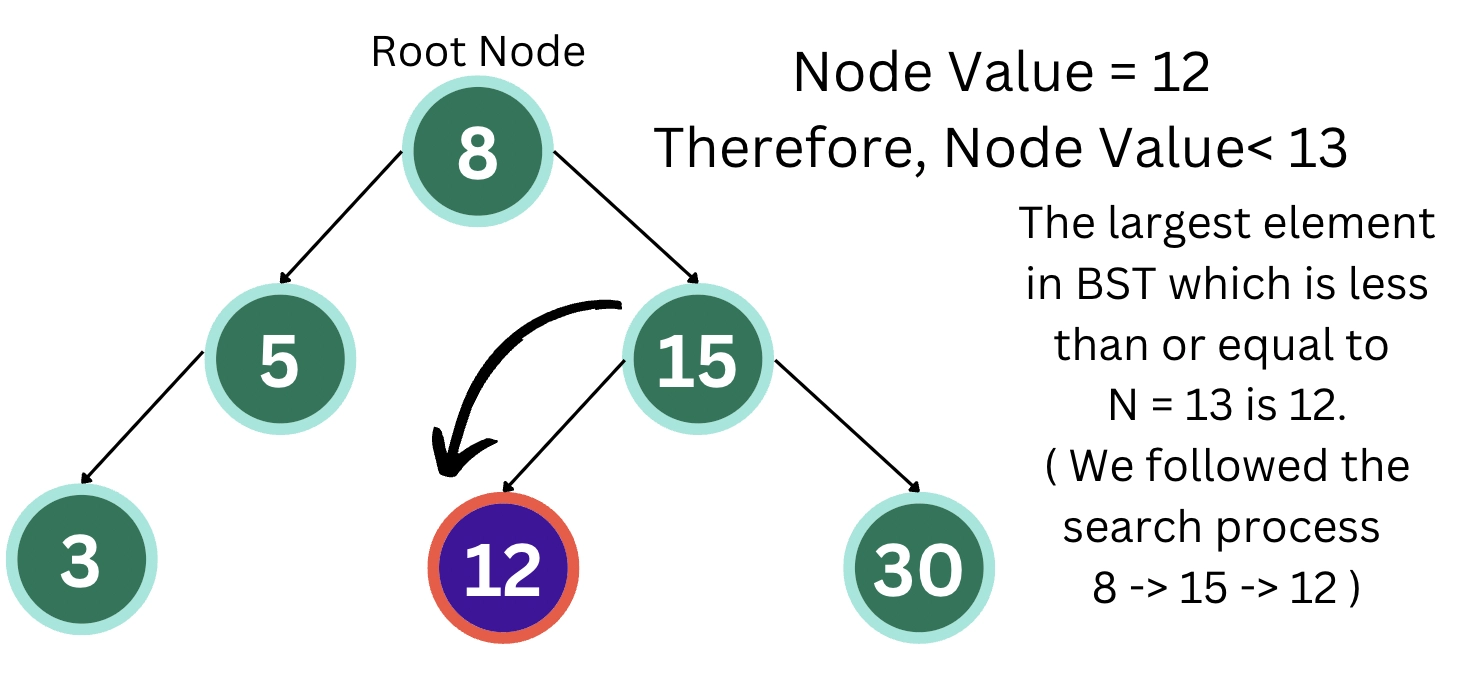
The output came out to be 12, the largest element after 13.
Code
// C++ program to find the largest number in BST which is less than or equal to N
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int key;
struct Node *left;
struct Node *right;
};
// Function to create a new Node in BST
Node* newNode(int val)
{
Node* temp = new Node;
temp->key = val;
temp->left = NULL;
temp->right = NULL;
return temp;
}
// Function to create a binary search tree
Node* buildTree(string str)
{
if (str.length() == 0 || str[0] == 'N')
return NULL;
vector<string> ip;
istringstream iss(str);
for (string str; iss >> str; )
ip.push_back(str);
// Creating the root of the tree
Node* root = newNode(stoi(ip[0]));
// Pushing the root to the queue
queue<Node*> queue;
queue.push(root);
// Starting from the second element
int i = 1;
while (!queue.empty() && i < ip.size())
{
// Getting and removing the front of the queue
Node* currNode = queue.front();
queue.pop();
// Getting the current node's value from the string
string currentVal = ip[i];
// If the left child is not null
if (currentVal != "N") {
currNode->left = newNode(stoi(currentVal));
queue.push(currNode->left);
}
// For the right child
i++;
if (i >= ip.size())
break;
currentVal = ip[i];
// If the right child is not null
if (currentVal != "N") {
currNode->right = newNode(stoi(currentVal));
queue.push(currNode->right);
}
i++;
}
return root;
}
void findMaxValue(Node* root,int N,int &maxValue){
if(root==NULL)
{
return;
}
findMaxValue(root->left,N,maxValue);
findMaxValue(root->right,N,maxValue);
if(root->key<=N)
{
maxValue=max(maxValue,root->key);
}
}
int findLargestNumberinBST(Node* root, int N)
{
int maxValue=-1;
findMaxValue(root, N, maxValue);
return maxValue;
}
int main()
{
cout << "Enter number of test cases: ";
int t;
cin >> t;
for(int i=1; i<=t; i++)
{
cout << "\nTest Case " << i << "\n";
string s;
cout << "Enter elements into BST:\n";
getline(cin >> ws, s);
cout << "Enter the number N: ";
int x;
cin >> x;
Node* root = buildTree(s);
cout << "The largest number in BST which is less than or equal to N: ";
cout << findLargestNumberinBST(root, x) << endl;
}
return 1;
}

You can also try this code with Online C++ Compiler
Output

Time and Space Complexities
Let us discuss the time and space complexity of the problem: To find the largest number in BST which is less than or equal to N.
Time Complexity

The time complexity for the given problem is O(H), where H is the height of the binary search tree taken by the user.
Space Complexity

The auxiliary space complexity for the given problem is O(H), where H is the height of the binary search tree taken by the user.
You can also read about insertion into bst.
Frequently Asked Questions
Describe the binary tree.
A binary tree is a data structure that can have a maximum of two children. Since a binary tree can only have two children, we usually refer to them as the left and right children.
What is a binary search tree?
A binary search tree is a binary tree in which all of the nodes to the left of the root node have values less than the root node, and all of the nodes to the right of the root node have values greater than the root node.
What is a Full Binary Tree?
A full binary tree is a type of binary tree in which every parent and the internal node has either two or no children.
How can one find the largest number in BST?
We can find the largest number in BST by traversing through the right subtree of each node we come across until we reach the rightmost node. In BST, the rightmost node is the largest number.
What is the maximum height of a BST having N number of nodes?
If a binary search tree has ‘N’ number of nodes, the maximum height it can have is (N-1).
Conclusion
In this article, we covered all about the DSA problem to find the largest number in BST which is less than or equal to N. We discussed the algorithm, code, and dry run, along with the time and space complexities for the problem of finding the largest number in BST which is less than or equal to N.
Check out this problem - Longest Common Prefix
If you would like to learn more about these problems, check out our related articles on-
Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, JavaScript, System Design, DBMS, Java, etc. Enroll in our courses and refer to the mock test and problems available. Take a look at the interview experiences and interview bundle for placement preparations.
Happy Learning, Ninja!🥷✨