Introduction
A graph is a type of non-linear data structure made up of vertices and edges. The vertices are also known as nodes, and edges are lines or arcs that connect any two nodes in the graph.
Formally, a graph is a pair of sets (v, e), where e is the set of edges connecting the pairs of vertices and v is the set of vertices.
This blog will discuss the problem of finding the largest subset of Graph Vertices with Edges of 2 or more colors. We will discuss this article in detail. Let's start going!
Problem Statement
In this problem, we are given a complete undirected graph with N nodes or vertices in which the edges of the graph are colored. We are given a graph in the form of an adjacency matrix graph[][], where graph[i][j] is the color of the edge from vertex i to vertex j.
Sample Examples
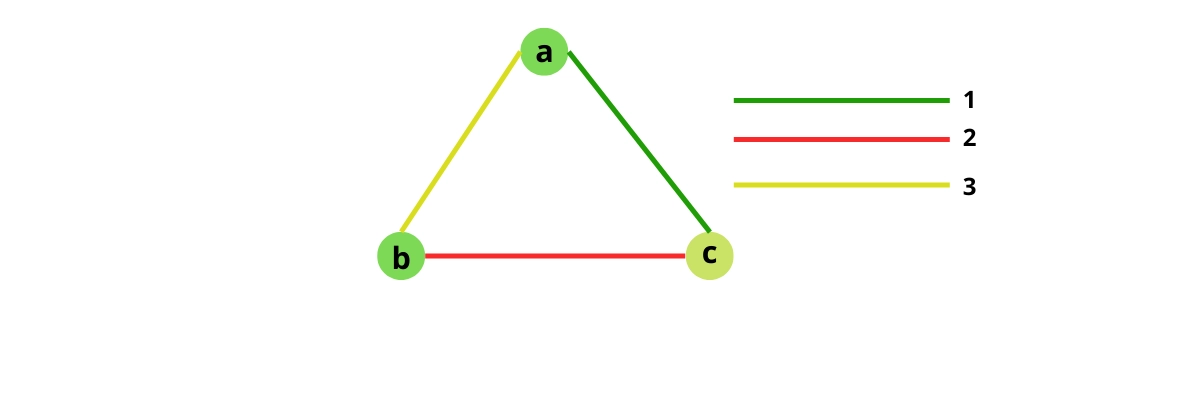
Example 1:
Input:
graph[][3]= {{0,2, 1},
{2, 0, 3},
{1, 3, 0}} Output:
3
Explanation: All the nodes in the adjacency matrix have different color edges than one.
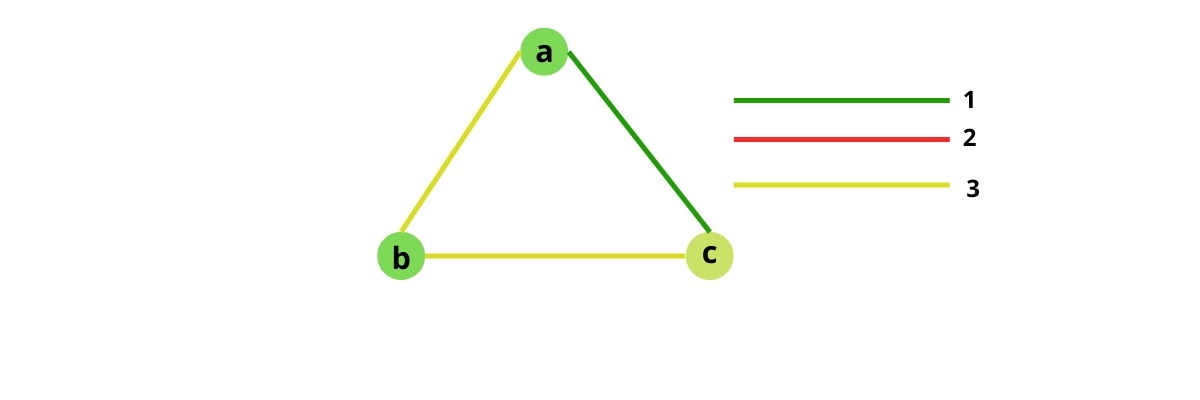
Example 2:
Input:
graph[][3]= {{0,2, 1},
{2, 0, 3},
{1, 1, 0}} Output:
1
Explanation: Only one node in the adjacency matrix has different color edges than one.
Approach
We will traverse each and every node of the adjacent matrix and remove all the nodes having the same edge colors connected with different nodes. After removing all the nodes, return the count of the nodes having different color edges.
Algorithm
✔️ Create an adjacent matrix graph[i][j].
✔️ Insert the vertices in a set.
✔️ If the size of the set is 1, return 1.
✔️ Traverse the Adjacent Matrix, and if the row and column index is not the same, insert them into a new set.
✔️ If the size of the new set is 1, remove the row index from the old set and return the size of the set.
Implementation
C++ Program to find the largest subset of Graph Vertices with Edges of 2 or more colors.
#include <bits/stdc++.h>
using namespace std;
int largest_subset(int graph[][3])
{
set<int> v;
for (int i = 0; i < 3; i++)
{
v.insert(i);
}
while (!v.empty())
{
if (v.size() == 1)
{
return 1;
}
bool removed= false;
for (int x : v)
{
set<int> val;
for (int z : v)
{
if (z != x)
{
val.insert(graph[x][z]);
}
}
if (val.size() == 1)
{
v.erase(x);
removed = true;
break;
}
}
if (!removed)
{
break;
}
}
return v.size();
}
int main()
{
int graph[][3] = {{0,2,1}, {2,0,3}, {1,3,0}}
cout <<largest_subset(graph)<<endl;
return 0;
}Output:
3Time Complexity
The time complexity of the above approach for the problem of finding the largest subset of graph vertices with edges of 2 or more colors is O(n^3), as we have to visit every node of the graph matrix.
Space Complexity
The space complexity of the above approach for the problem of finding the largest subset of graph vertices with edges of 2 or more colors is O(n), as we are using extra space for storing the vertices in the set.




