Example📎
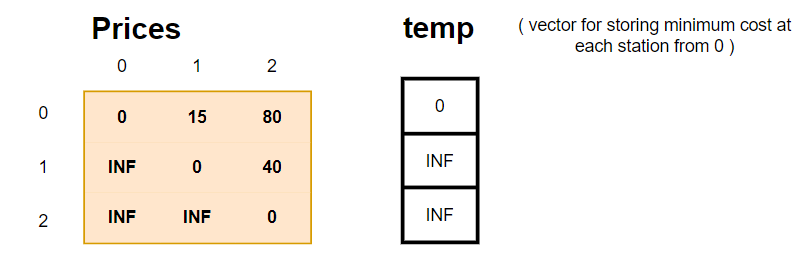
If ‘N’ = 3 ->
'PRICE[3][3]' = {{0, 15, 80,},
{INF, 0, 40},
{INF, INF, 0}};
First, go from 1st station to 2nd at 15 costs, then go from 2nd to 3rd at 40. 15 + 40 = 55 is the total cost.It is cheaper than going directly from station 1 to station 3 as it would have cost 80.
The output will be 55.
Input Format:
The number of test cases is indicated by the integer "T" on the first line of the input.
Each test case starts off with a single integer, "N," denoting the number of rows and columns in the "PRICE" matrix.
The following "N" lines are listed: The cost of pairings (i,j) is represented by "N" space-separated numbers on each line, where I and "j" are the indices of the "PRICE" matrix.
Output Format:
For each test case, return the minimum price that will have to be paid such that the train reaches from 1st to 'N'th station.
Print the output for each test case in a separate line.
Note:
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 100
1 <= N <= 1000
Time Limit: 1 sec
Approach⛏️
In order to find the minimum cost to reach the destination using a train, we are using a temp to store the intermediate values during the process. This problem requires some dynamic programming techniques.
Algorithm
Algorithm of the function minCost() that is being used to determine the minimum cost:
/*
temp array for storing minimum value for each station.
*/
int temp[N];
/*
turning minimum value to max initially except for the first station, because it cost 0 to reach 0th station from 0th station ;)
*/
for i=1 to N:
temp[i] = INT_MAX
temp[0] = 0
/*
Check each station to see if utilizing it as an intermediate station provides a better route.
*/
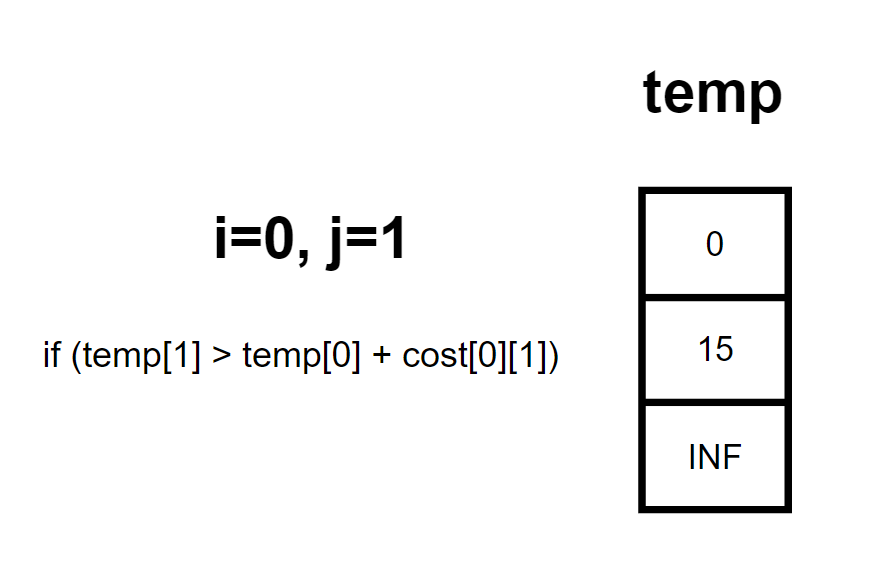
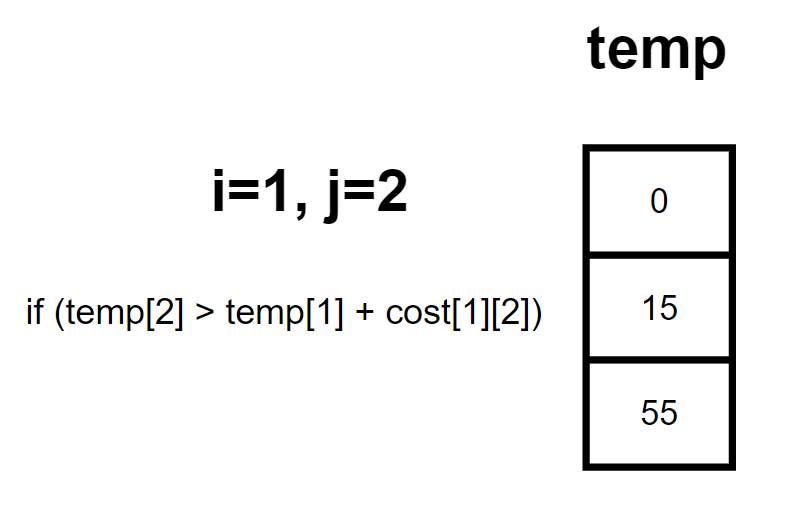
for i=0 to N:
for j=i+1 to N:
if temp[j] > temp[i]+cost[i][j]:
temp[j] = temp[i]+cost[i][j]
/*
at, return the last element
*/
return temp[N-1]

Implementation in C++
/*
C++ Solution of the problem “Find the minimum cost to reach the destination using a train”
Dynamic programming solution to find the minimum cost to reach the destination using a train
*/
#include<bits/stdc++.h>
using namespace std;
#define INF INT_MAX
#define N 3
//This function returns the least expensive way to go from station 0 to station N-1.
int minCost(int price[][N]) {
// temp[i] stores the least expensive way to travel from station 0 to station i.
int temp[N];
for (int i=0; i<N; i++)
temp[i] = INF;
temp[0] = 0;
/*
Check each station to see if using it as an intermediate station will provide the best route.
*/
for (int itr=0; itr<N; itr++)
for (int j_itr=i+1; j_itr<N; j_itr++)
if (temp[j_itr] > temp[itr] + cost[itr][j_itr])
temp[j_itr] = temp[itr] + cost[itr][j_itr];
return temp[N-1];
}
// Driver program to test the above function
int main() {
int price[N][N] = {{0, 15, 80,},
{INF, 0, 40},
{INF, INF, 0}};
cout<< "The least expensive way to get to the station"<< N << " is " << minCost(cost);
return 0;
}

You can also try this code with Online C++ Compiler
Time Complexity ⌛

The time complexity of the problem “Find the minimum cost to reach the destination using a train” using the above approach is O(N*N), where N is the number of stations.
Space Complexity 🚀

The space complexity of the problem “Find the minimum cost to reach the destination using a train” using the above approach is O(N) as we are storing the answer in the custom array.
Check out Longest Common Substring
Frequently Asked Questions
Which two forms of dynamic programming are there?
Optimization problems and combinatorial issues are the two categories under which Dynamic Programming problems fall.
What exactly is dynamic programming used for?
When we have difficulties that can be broken down into smaller, related problems so that the solutions can be reused, we employ dynamic programming. These algorithms are typically employed for optimization.
What is a Full Binary Tree?
A full binary tree is a particular kind of binary tree in which every parent node and internal node either has two children or none at all.
What benefits does binary search offer?
Because the amount of data to be searched is reduced by half with each step in a binary search, one of its key benefits is that it is faster than a serial search.
Where does dynamic programming actually get used?
Computer networks, routing, graph issues, computer vision, artificial intelligence, machine learning, etc. all make extensive use of dynamic programming.
Conclusion💡
In this article, we have discussed a coding problem in which we have to Find the minimum cost to reach the destination using a train. We have seen the question's solution, time, and space complexity.
If you think this blog has helped you enhance your knowledge about the above question, and if you want to learn more, check out our articles.
And many more on our website.
Visit our website to read more such blogs. Make sure that you enroll in the courses we provide, take mock tests, solve problems available, and interview puzzles. Also, you can pay attention to interview stuff- interview experiences and an interview bundle for placement preparations.











