Find the number of connected grids of a given size in a 2D-Matrix

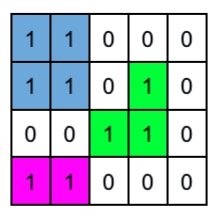
Approach

Do a DFS traversal on the matrix, find the number of cells in each component, and store their frequency in a hashmap. You can go through this article for further reference to a DFS Traversal in a 2D Matrix.

Code in C++

#include<iostream>
#include<vector>
#include<unordered_map>
using namespace std;

// This function will return the number of connected cells around the starting [i,j]
int dfs(vector<vector<int> >& visited,vector<vector<int>>& grid,int i,int j){
	if(i<0 || j<0 || i>=grid.size() || j>=grid[i].size()){
		return 0; // If we go out of the matrix, then no connected cell
    }

    // If the cell has been already visited or if the cell is marked as 0, then don't
    // need to visit this cell.
    if(visited[i][j]==true || grid[i][j]==0){
        return 0;
    }

    visited[i][j]=true;

    // Travel on the connected cells
    int connectedCells = 1;
    connectedCells += dfs(visited,grid,i+1,j);
    connectedCells += dfs(visited,grid,i-1,j);
    connectedCells += dfs(visited,grid,i,j+1);
    connectedCells += dfs(visited,grid,i,j-1);
    return connectedCells;
}

// This function will return the frequency of each size of a connected grid present in the matrix
unordered_map<int,int> findFrequency(vector<vector<int>>& grid) {
    unordered_map<int,int> ans;

    // First making a visited array to maintain the cells already visited during the DFS call.
    vector<vector<int> > visited(
    	grid.size(),
    	vector<int>(grid[0].size(),false)
    );

    for(int i=0;i<grid.size();i++){
        for(int j=0;j<grid[i].size();j++){
            if(visited[i][j]==false && grid[i][j]==1){
            	// Count the number of cells in this connected 
            	// grid and update its size in the hashmap
                int count = dfs(visited,grid,i,j);
                ans[count]++;
            }
        }
    }

    return ans;
}

int main(){
	vector<vector<int> > grid{
		{1,1,1,1,1,1},
		{1,1,0,0,0,0},
		{0,0,0,1,1,1},
		{0,0,0,1,1,1},
		{0,0,1,0,0,0},
		{1,0,0,0,0,0},
	};

	vector<int> queries{6 , 1 , 8, 2};

	unordered_map<int,int> frequencyCount = findFrequency(grid);
	for(int i=0;i<queries.size();i++){
		cout<<frequencyCount[queries[i]]<<endl;
	}
}

You can also try this code with Online C++ Compiler

Run Code

Output

1
2
1
0

Time Complexity 

Since time complexity will be O(1) for each query, time complexity = O(Q) where Q = number of queries. The time complexity for precomputing each connected grid's size will be O(n*m), where n is the number of rows and m is the number of columns in the matrix.

Space Complexity 

We are making a hashmap that will store the frequency of the number of times a particular size of the connected component occurs. Since the size of the connected component can vary from 1 to n*m, the space complexity due to this hashmap will be O(n*m), where n is the number of rows and m is the number of columns in the matrix.

Frequently Asked Questions

1. What is the difference between a tree and a graph?
   Trees and graphs are different since there can never be loops in a tree, but we can have loops in a graph. Also, all the nodes in a tree are always connected, but that is not true for a graph.
    
2. What is the difference between a DFS Traversal and a BFS Traversal?
   In a DFS traversal of a graph, we begin from any random node and travel down each branch as feasible before returning to the current node. In contrast, in a BFS traversal, we visit each node at the current level before visiting their children nodes. 
   DFS Traversal is performed using a stack, whereas a BFS Traversal is performed using a queue.
    
3. Are there more Data Structures and Algorithms problems in Coding Ninjas Studio?
   Yes, Coding Ninjas Studio is a platform that provides both practice coding questions and commonly asked interview questions. The more we'll practice, the better our chances are of getting into a dream company of ours.

Key Takeaways

In this article, we learned to do a DFS traversal on a 2D Matrix and calculate the size of the connected components.

Since graphs are frequently asked in interviews, we recommend you practice more problems based on graphs on Coding Ninjas Studio. 

Check out this problem - Matrix Median

Are you planning to ace the interviews of reputed product-based companies like Amazon, Google, Microsoft, and more? Attempt our Online Mock Test Series on Coding Ninjas Studio now!