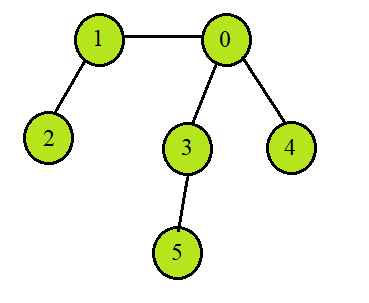
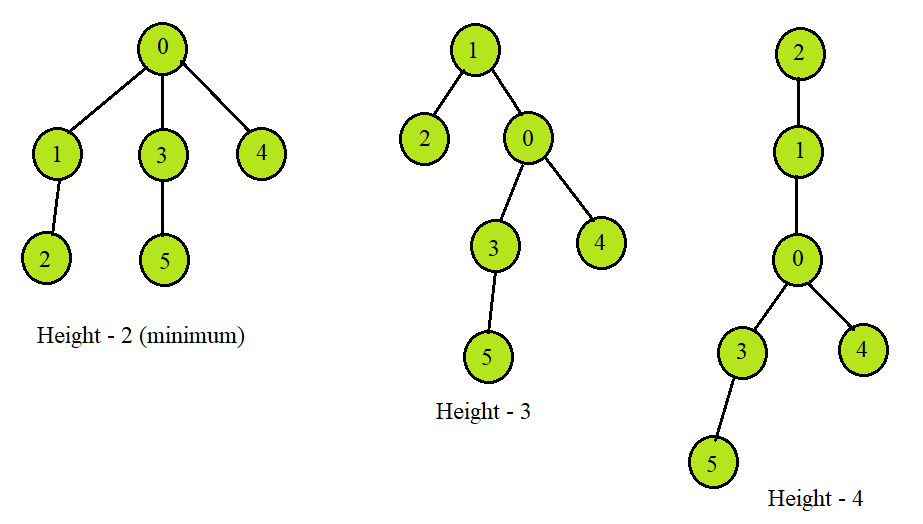
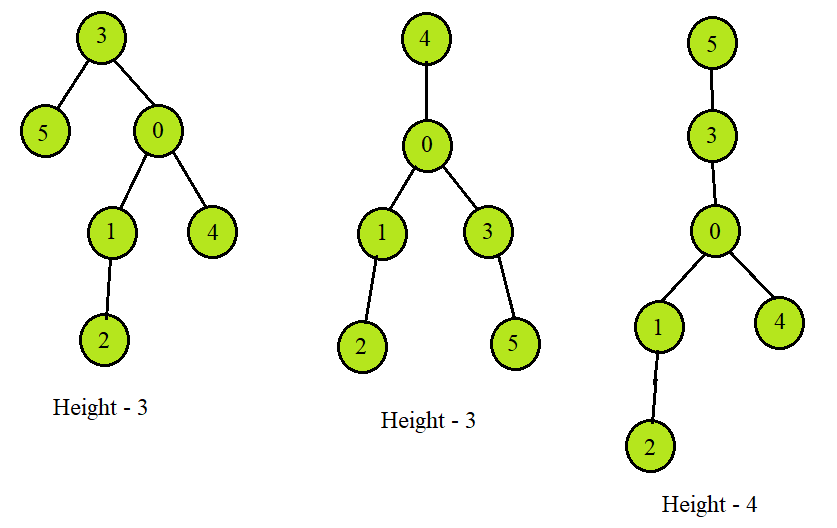
Solution 💡
The solution to the problem is to find the longest path between two leaf nodes. The middle node of such a path will give us the node that, when taken as the root node, will have the minimum height. We can find the longest path; if the number of nodes is even, there will be two central nodes, hence two nodes with minimum height. But if the number of nodes is odd, only one node will have the minimum height.

The algorithm of the solution is given below:
- Initialize and declare a graph for which you need to find the roots of a tree that gives minimum height.
- Use an adjacency list to represent the edges of a graph. Maintain a degree vector to keep track of the degree of each node of the graph.
- Initialize a queue and enqueue all the leaf nodes to it. Delete those nodes from the graph.
-
At max, there can be two vertices with minimum height, so loop until you have two vertices.
- Consider each node from the queue once.
- Decrement the degree of each neighbor of the current node. Enqueue the neighbor in the queue if it becomes a leaf node.
- At last, the queue will have one or two nodes, our result.
- Print the results.
C++ Implementation 📌
#include <bits/stdc++.h>
#include<vector>
#include<queue>
using namespace std;
/* Graph class is used to create a graph and represent edges as an adjacency list */
class Graph
{
public:
int num_of_vertices;
/* Initializing a pointer for adjacency list */
vector<int> *adj;
vector<int> degree;
/* Declaring Constructor of the class */
Graph(int num)
{
/* Initializing important variables */
this->num_of_vertices = num;
adj = new vector<int>[num_of_vertices];
/* Initializing the degree of each node as 0 */
for (int i = 0; i < num_of_vertices; i++)
degree.push_back(0);
}
/* Helper function to add an edge to the graph */
void AddEdge(int v1, int v2)
{
/* adding the edge in adjacency list*/
adj[v1].push_back(v2);
adj[v2].push_back(v1);
/* Incrementing the degree of both vertices by 1 */
degree[v1]++;
degree[v2]++;
}
/* Function to find the roots of a tree with minimum weight */
vector<int> MinimumHeight()
{
queue<int> q;
/* Add all the leaf nodes to the queue */
for (int iter = 0; iter < num_of_vertices; iter++)
if (degree[iter] == 1)
q.push(iter);
/* At max, there can be two vertices with minimum height, so loop until you have two vertices */
while (num_of_vertices > 2)
{
/* Already added some vertices to the queue, so remove those from the total vertices count.*/
num_of_vertices = num_of_vertices - q.size();
int tmp=q.size();
for (int i = 0; i < tmp; i++)
{
/* Consider each node in queue once */
int root = q.front();
q.pop();
/* Decrement the degree of each neighbor of root and enqueue to the queue if it becomes a leaf node */
for (auto current_node = adj[root].begin(); current_node != adj[root].end(); current_node++)
{
degree[*current_node] -= 1;
if (degree[*current_node] == 1)
q.push(*current_node);
}
}
}
/* Copy the answer to a vector */
vector<int> roots;
while (!q.empty())
{
roots.push_back(q.front());
q.pop();
}
/* Returning the answer to the main function*/
return roots;
}
};
/* Driver Function */
int main()
{
/* Initializing and Declaring the given graph*/
Graph graph(6);
graph.AddEdge(0, 1);
graph.AddEdge(0, 3);
graph.AddEdge(0, 4);
graph.AddEdge(1, 2);
graph.AddEdge(5, 3);
/* Calling the Function to find the roots of a tree with minimum height and storing the result in roots variable*/
vector <int> roots = graph.MinimumHeight();
/* Printing the results*/
for (int node = 0; node < roots.size(); node++)
cout << roots[node] << " ";
return 0;
}

You can also try this code with Online C++ Compiler
Python Implementation 📌
from queue import Queue
'''Graph class is used to create a graph and represent edges as an adjacency list'''
class Graph:
'''Declaring Constructor of the class'''
def __init__(self, num_of_vertices):
'''Intializing important structures '''
self.num_of_vertices = num_of_vertices
self.degree = [0 for i in range(num_of_vertices)]
self.adj = dict((i, []) for i in range(num_of_vertices))
'''Helper function to add an edge to the graph '''
def AddEdge(self, v1, v2):
'''adding the edge in adjacency list'''
self.adj[v1].append(v2)
self.adj[v2].append(v1)
'''Incrementing the degree of both vertices by 1 '''
self.degree[v1] += 1
self.degree[v2] += 1
''' Function to find the roots of a tree with minimum height'''
def MinimumHeight(self):
q = Queue()
'''Add all the leaf nodes to the queue'''
for iter in range(self.num_of_vertices):
if self.degree[iter] == 1:
q.put(iter)
'''At max, there can be two vertices with minimum height, so loop until you have two vertices. '''
while (self.num_of_vertices > 2):
''' Already added some vertices to queue, so remove those from total vertices count.'''
self.num_of_vertices = self.num_of_vertices - q.qsize()
tmp = q.qsize()
for i in range(tmp):
''' Consider each node in quere once '''
root = q.get()
'''Decrement the degree of each neighbor of root and enqueue to the queue if it becomes a leaf node'''
for current_node in self.adj[root]:
self.degree[current_node] -= 1
if self.degree[current_node] == 1:
q.put(current_node)
'''Copy the answer to a vector'''
roots = []
while q.qsize() > 0:
roots.append(q.get())
''' Returning the answer to the main function'''
return roots
''' Driver Function '''
def main():
''' Initializing and Declaring the given graph'''
graph = Graph(6);
graph.AddEdge(0, 1);
graph.AddEdge(0, 3);
graph.AddEdge(0, 4);
graph.AddEdge(1, 2);
graph.AddEdge(5, 3);
''' Calling the Function to find the roots of a tree with minimum height and storing the result in roots variable'''
roots = graph.MinimumHeight();
''' Printing the results'''
for root in roots:
print(root, end = ' ')
'''Executing Main'''
main()

You can also try this code with Online Python Compiler
Output
0
Complexities 📈
Time Complexity ⏳
O(N), Where N denotes the count of nodes in the tree.
Reason: The time complexity is O(N) because we consider each node only once.
Auxiliary Space Complexity 💾
O(N+ K), where N denotes the count of nodes in the graph and K denotes the number of edges.
Reason: We are using an adjacency list to represent the graph, which takes O(N+K) additional space. Other than this, the vector to store the degree of each node and the queue is also used with can take a maximum of N elements at a time. So Auxiliary space complexity of the above program is O(N+K) + O(N) + O(N), which is equal to O(N+K).
Frequently Asked Questions
What is a graph?
A graph is a data structure used to represent highly correlated data. A graph is made up of vertices and edges. The edges are used to connect the vertices based on some relationship.
What is a tree?
A Tree is a non-linear data structure similar to a graph that stores data hierarchically. A tree is an undirected graph with no cycles. Each tree has a root node and edges that connect the root node with its child nodes.
What is the height of a tree?
The height of a tree is referred to as the length of the path of the furthest leaf node from the tree's root. In order words, it is also given by the number of levels present in the tree.
What are a root and a leaf node in a tree?
The root node of a tree is the master node with which the tree begins. It has no incoming edges. The leaf node or terminal node is the child node of a tree that does not have any child. The outdegree of such nodes is 0.
Why do we calculate the complexities of a program?
Complexities of a program are used to compare two or more approaches to solve the same problem. It provides a measure to compare and find a more efficient solution in terms of time and space.
Conclusion
This article discussed the algorithm and implementation to find the roots of a tree that gives minimum height. To learn more about tree data structure, visit, Introduction to Trees - Coding Ninjas Coding Ninjas Studio.
I hope you would have gained a better understanding of these topics now!
Check out this problem - Check If A String Is Palindrome
Are you planning to ace the interviews with reputed product-based companies like Amazon, Google, Microsoft, and more?
Attempt our Online Mock Test Series on Coding Ninjas Studio now!
Happy Coding!