Find the S-value of the Given Subarrays Using Mo’s Algorithm

Sample Test Cases

Input:  8 5
		2 1 3 3 1 5 5 3
		1 2
		2 4
		6 8
		8 8
		1 8

Output: 3 13 23 3 53 

Explanation: 

In the range [1, 2], the frequency of 1 is 1, and the frequency of 2 is 1. So, S-value = freq[1] * freq[1] * 1 + freq[2] * freq[2] * 2 = 1 * 1 * 1 + 2 * 1 * 1 = 3.

In the range [2, 4], the frequency of 1 is 3, and the frequency of 3 is 2. So, S-value = freq[1] * freq[1] * 1 + freq[3] * freq[3] * 3 = 1 * 1 * 1 + 3 * 2 * 2 = 13. 

In the range [6, 8], the frequency of 5 is 2, and the frequency of 3 is 1. So, S-value = freq[5] * freq[5] * 5 + freq[3] * freq[3] * 3 = 2 * 2 * 5 + 3 * 1 * 1 = 23.

In the range [8, 8], the frequency of 1 is 1. So, S-value = freq[3] * freq[3] * 3 = 3.

In the range [1, 8], the frequency of 1 is 2, the frequency of 3 is 3, the frequency of 5 is 2, and the frequency of 2 is 1. So, S-value = 1 * 2 * 2 + 3 * 3 * 3 + 5 * 2 * 2 + 2 * 1 * 1 = 53

Check out Euclid GCD Algorithm

Approach

We highly recommend you to go through this blog once before going to the solution.

Brute force

The most straightforward approach to solve this problem is to run a loop from i = l to i = r and calculate the frequency of every element in the subarray a[l],a[l + 1], a[l + 2],.........,a[r]. Then by using the frequency, we can calculate the S-value of subarray a[l],a[l + 1], a[l + 2],.........,a[r].

The time complexity of this approach is O(Q * N). If N = 10^5 and Q = 10^5, then in the worst-case, the total number of operations is 10^10, which is inefficient.

Efficient Approach

Mo's algorithm can solve this problem efficiently (sqrt decomposition). 

The idea is to answer the queries in a particular order to reduce the number of operations. For that, we will divide the array into the ⌈√N ⌉ block, each of size ⌈√N ⌉ (except the last block) then we will first answer all the queries having left index in the 0th block, then queries having left index in 1st block and so on. In a particular block, we will answer the queries according to the right index (a query having a smaller right index will be answered first).

If block_size be the size of each block (block_size = ⌈√N ⌉), then we will sort the queries according to the value of ⌊l/block_size⌋. If the value of ⌊l/block_size⌋ is the same for the two queries, we will sort according to the value of the right index.

For the sample test case :

 ⌈√N ⌉  = 3

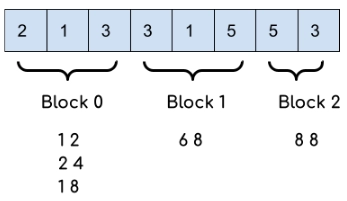
Queries : {1, 2, 1

                  2, 4, 2

                  1, 8, 5

        6, 8, 3

        8, 8, 4 }

How to shift from one range to the next??

Suppose [cl, cr] be the current range and x be the answer of this range. Now, if we want to shift to the range [l, r], then there are four conditions - 

1. l > cl - remove the range [cl, l - 1]
2. l < cl - add the range [l, cl - 1]
3. r > cr - add the range [cr + 1, cr]
4. r < cr - remove the range [r + 1, cr]

How to remove/add the element at index u??

If freq[a[u]] be the current frequency of a[u], then to remove, subtract a[u] * freq[a[u]] * freq[a[u]] from the current answer, decrement freq[a[u]] by one, then add a[u] * freq[a[u]] * freq[a[u]] to the current answer.

And to add, subtract a[u] * freq[a[u]] * freq[a[u]] from the current answer, increment freq[a[u]] by one, then add a[u] * freq[a[u]] * freq[a[u]] to the current answer.

Code

#include <bits/stdc++.h>
using namespace std;
const int block_size = 750;
const int M = 1000007;
//given array, array to store the frequency
int a[M], freq[M];
//variable to store the answer
long long fin_answer;
//to store query
struct query {
   int l, r, idx;
};
//comparator to sort the given queries
bool cmp(query &x, query &y){
   //sort the queries according to the value of ⌊l/block_size⌋
   if(x.l/block_size != y.l/block_size)
       return x.l/block_size < y.l/block_size;
   //if block is same sort according to right index
   else
       return x.r < y.r;
}
//function to add
void add(int p){
   fin_answer -= (long long)p * freq[p] * freq[p];
   //increment the frequency
   ++freq[p];
   fin_answer += (long long)p * freq[p] * freq[p];
}
//function to remove
void remove(int p){
   fin_answer -= (long long)p * freq[p] * freq[p];
   //decrement the frequency
   --freq[p];
   fin_answer += (long long)p * freq[p] * freq[p];
}
//Mo’s algorithm
vector <long long> MO(vector <query> &queries){
   int Q = queries.size();
   vector <long long> answers(Q);
   //sorting the queries using the comparator
   sort(queries.begin(), queries.end(), cmp);
   //left pointer, right pointer
   int cl = 0, cr = -1;
   for(auto u : queries){
       //l < cl - add the range [l, cl - 1]
       while(cl > u.l){
           --cl;
           add(a[cl]);
       }
       //r > cr - add the range [cr + 1, cr]
       while(cr < u.r){
           ++cr;
           add(a[cr]);    
       }
       //l > cl - remove the range [cl, l - 1]
       while(cl < u.l){
           remove(a[cl]);
           ++cl;
       }
       //r < cr - remove the range [r + 1, cr]
       while(cr > u.r){
           remove(a[cr]);
           --cr;
       }
       //store the current answer
       answers[u.idx] = fin_answer;
   }
   return answers;
}
signed main()
{  
   //array's size, number of queries
   int n, t;
   cin >> n >> t;
   for(int i = 1; i <= n; ++i)
       cin >> a[i];
   //vector to store queries
   vector <query> query(t);
   for(int i = 0; i < t; ++i){
       //left index, right index
       int l, r;
       cin >> l >> r;
       query[i].l = l;
       query[i].r = r;
       //store the index of the query
       query[i].idx = i;
   }
   //function call
   vector <long long> answers = MO(query);
   //print the answers
   for(auto u : answers)
       cout << u << " ";
   cout << "\n";
   return 0;
}

Input

8 5
2 1 3 3 1 5 5 3
1 2
2 4
6 8
8 8
1 8

Output

3 13 23 3 53

Time Complexity

The time complexity is O((N + Q)√N).

Space Complexity

The space complexity is O(N + Q).

FAQs

1. Why are we using 350 as a block size instead of ⌈√N ⌉??  
   We declared block size as a constant (350) because division by constant is more efficient (compiler optimization), which improves our solution's runtime.

Key Takeaways

This article solved an offline range query problem using the Mo's algorithm. Mo's algorithm is a powerful data structure that can help you to solve complex range query problems. Check out this coding ninjas blog to learn more about it.  
Check out this problem - Maximum Product Subarray

To learn more about such data structures and algorithms, Coding Ninjas Studio is a one-stop destination. This platform will help you to improve your coding techniques and give you an overview of interview experiences in various product-based companies by providing Online Mock Test Series and many more benefits.

Happy learning!