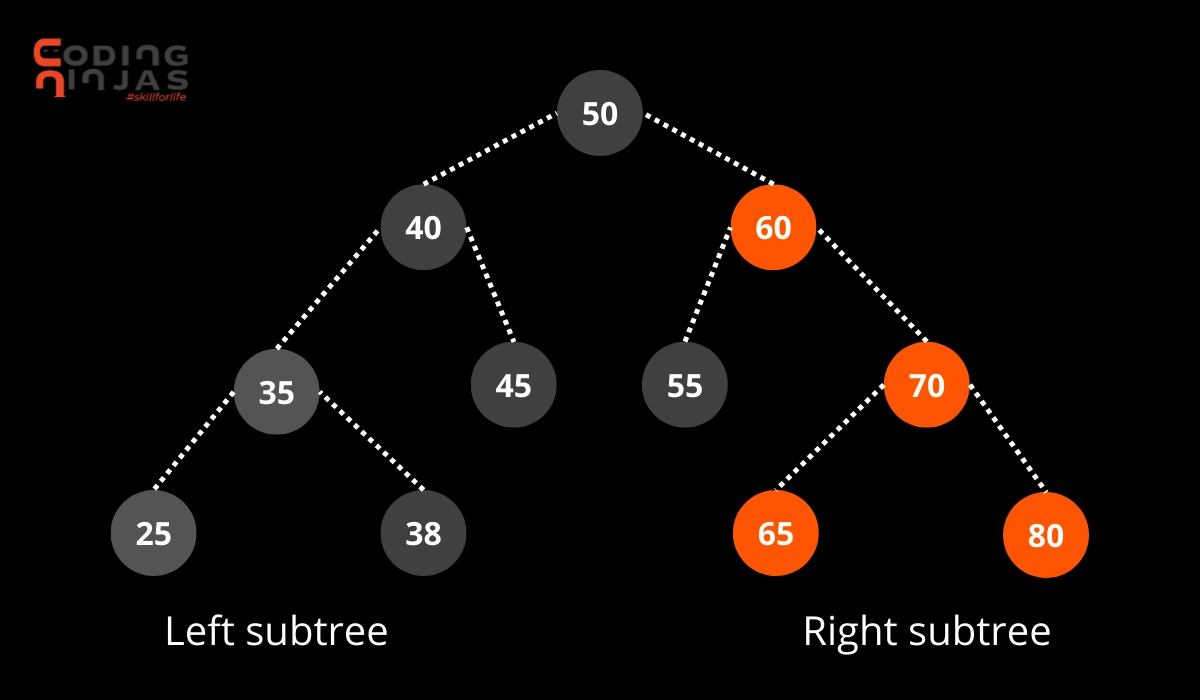
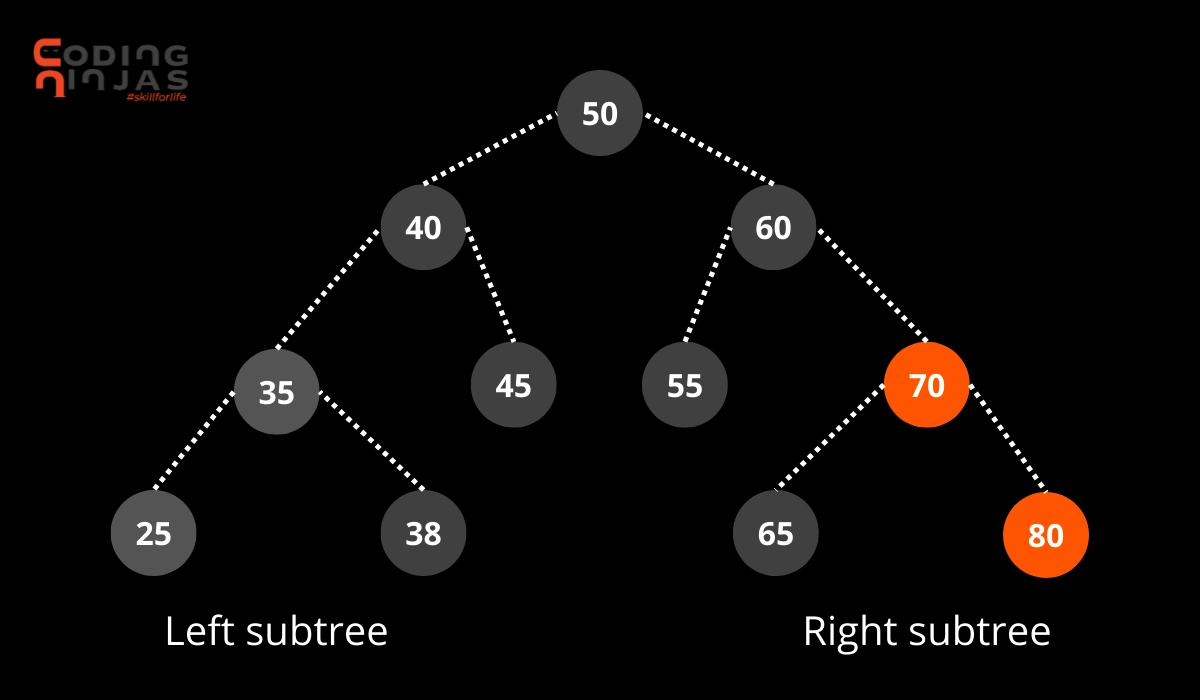
Algorithm
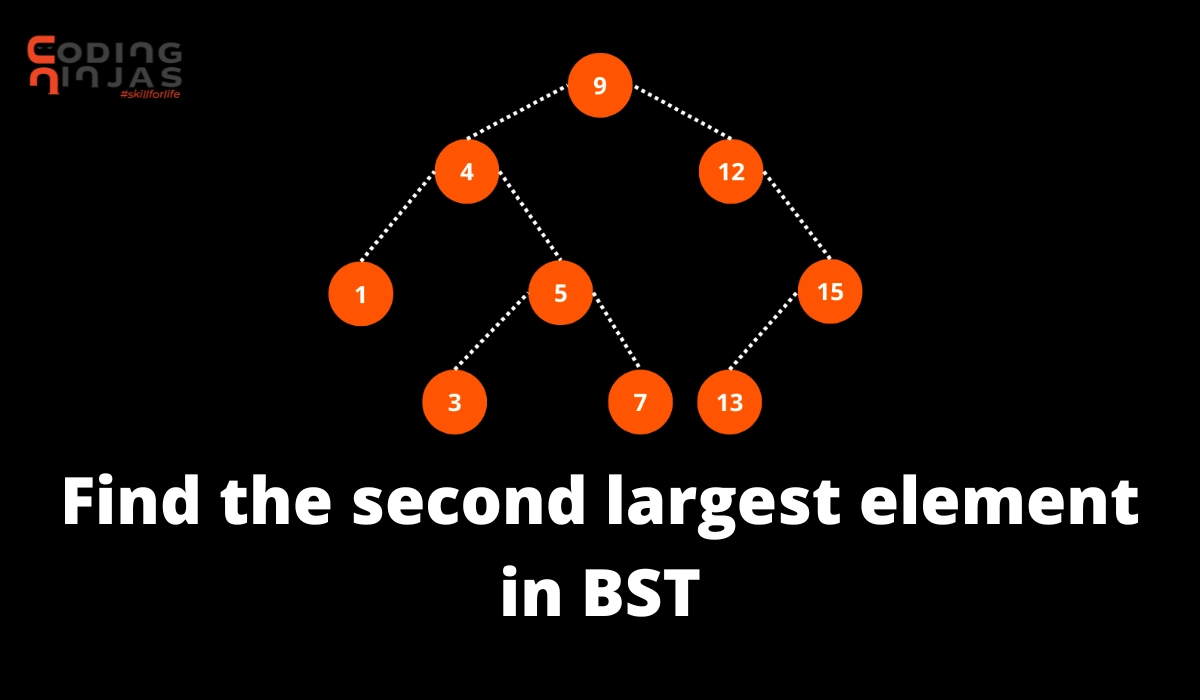
Following is the Algorithm to find the second largest element in BST:
-
Implement a Binary search tree.
-
Insert the values of the node into BST.
-
Traverse the nodes using the reverse inorder traversal method
-
Keep a count of the number of nodes being visited
-
Print the node once the count becomes 2.
Time complexity:
O(h) where h is the height of the Binary search tree.
Space Complexity:
O(n) for where n is the total number of nodes in the Binary search tree.
Implementation
Following is the Implementation to find the second largest element in BST:
C++
#include<bits/stdc++.h>
using namespace std;
struct Node
{
int key;
Node *left, *right;
};
// For creating a new BST node
Node *newNode(int item)
{
Node *tmp = new Node;
tmp->key = item;
tmp->left = tmp->right = NULL;
return tmp;
}
// To find the second largest element in a tree.
void secondLargestUtil(Node *root, int &c)
{
if (root == NULL || c >= 2)
return;
secondLargestUtil(root->right, c);
c++;
if (c == 2)
{
cout << "The second largest element is "
<< root->key << endl;
return;
}
secondLargestUtil(root->left, c);
}
// To find the second largest element
void secondLargest(Node *root)
{
int c = 0;
secondLargestUtil(root, c);
}
// To insert a new node in BST
Node* insert(Node* node, int key)
{
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
// Main functions
int main()
{
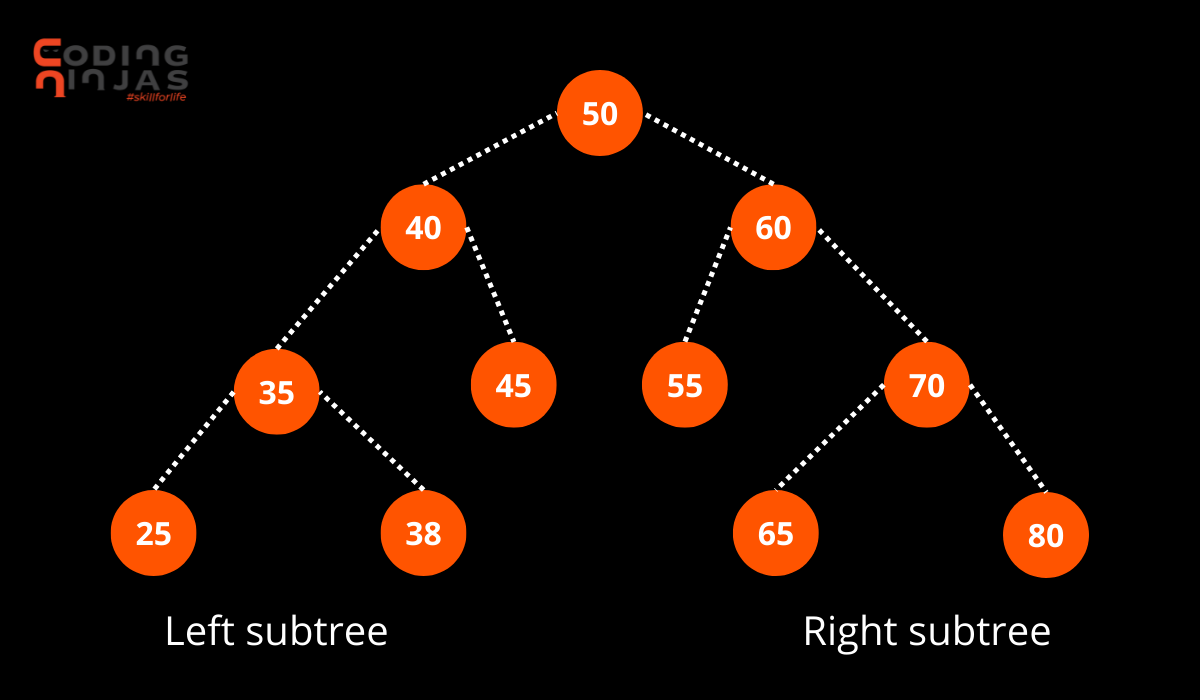
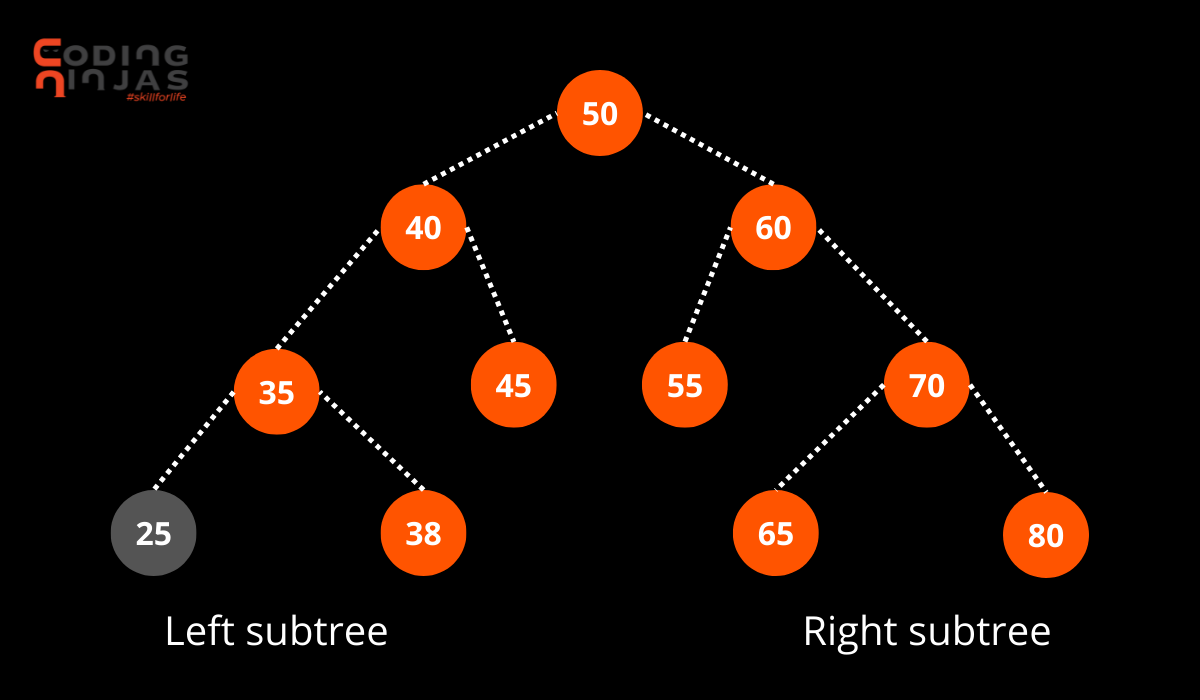
/* Let us create the following BST
50
/ \
40 60
/ \ / \
35 45 55 70 */
Node *root = NULL;
root = insert(root, 50);
insert(root, 40);
insert(root, 35);
insert(root, 45);
insert(root, 60);
insert(root, 55);
insert(root, 70);
secondLargest(root);
return 0;
}

You can also try this code with Online C++ Compiler
Output:
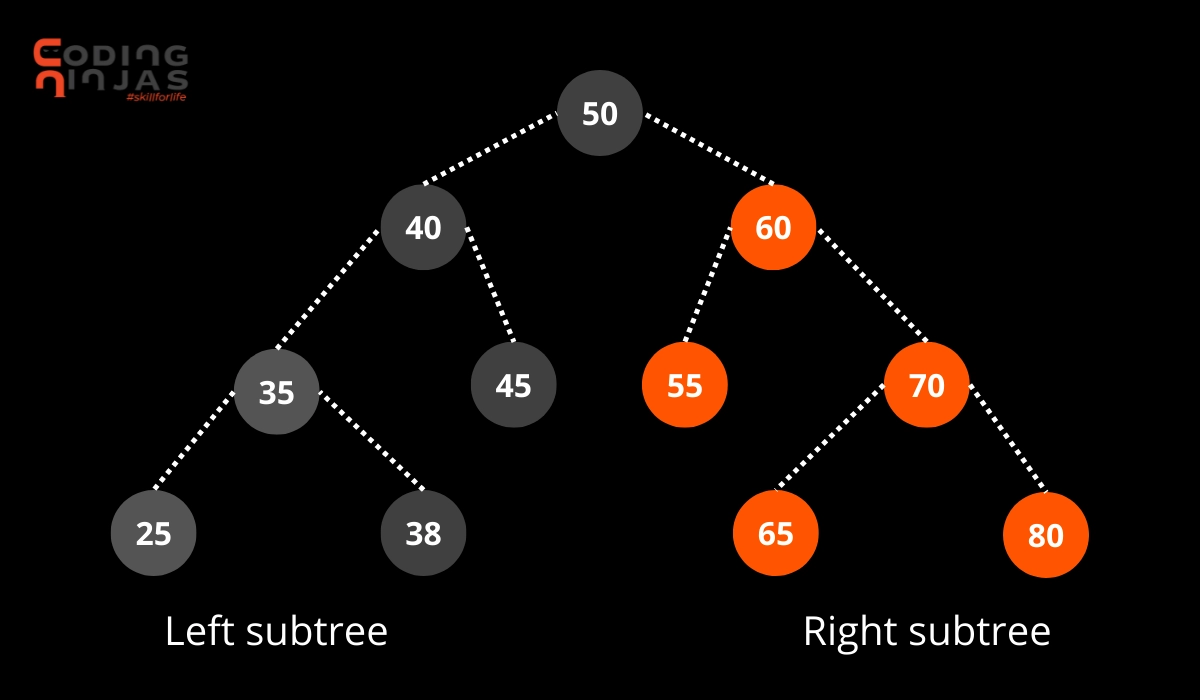
The second largest element is 60
PYTHON
# element in BST
class Node:
# Constructor for creating a new BST node
def __init__(self, data):
self.key = data
self.left = None
self.right = None
# To find the second largest element in a given tree.
def secondLargestUtil(root, c):
if root == None or c[0] >= 2:
return
secondLargestUtil(root.right, c)
c[0] += 1
if c[0] == 2:
print("The second largest element is", root.key)
return
secondLargestUtil(root.left, c)
# To find the second largest element
def secondLargest(root):
c = [0]
secondLargestUtil(root, c)
def insert(node, key):
if node == None:
return Node(key)
if key < node.key:
node.left = insert(node.left, key)
elif key > node.key:
node.right = insert(node.right, key)
return node
# Main Code
if __name__ == '__main__':
# Let us create the following BST
# 50
# / \
# 40 60
# / \ / \
# 35 45 55 70
root = None
root = insert(root, 50)
insert(root, 40)
insert(root, 35)
insert(root, 45)
insert(root, 60)
insert(root, 55)
insert(root, 70)
secondLargest(root)

You can also try this code with Online Python Compiler
Output:
The second largest element is 60
JAVA
// Java code to find the second largest element in BST
// For creating a new node
class Node {
int data;
Node left, right;
Node(int d)
{
data = d;
left = right = null;
}
}
class BinarySearchTree {
Node root;
BinarySearchTree()
{
root = null;
}
// For inserting new nodes
public void insert(int data)
{
this.root = this.insertRec(this.root, data);
}
Node insertRec(Node node, int data)
{
if (node == null) {
this.root = new Node(data);
return this.root;
}
if (data < node.data) {
node.left = this.insertRec(node.left, data);
} else {
node.right = this.insertRec(node.right, data);
}
return node;
}
public class count {
int c = 0;
}
// To find the second largest element
void secondLargestUtil(Node node, count C)
{
if (node == null || C.c >= 2)
return;
this.secondLargestUtil(node.right, C);
C.c++;
if (C.c == 2) {
System.out.print("The second largest element is "+
node.data);
return;
}
this.secondLargestUtil(node.left, C);
}
// To find the second largest element
void secondLargest(Node node)
{
count C = new count();
this.secondLargestUtil(this.root, C);
}
// Main function
public static void main(String[] args)
{
BinarySearchTree tree = new BinarySearchTree();
/* Let us create the following BST
50
/ \
40 60
/ \ / \
35 45 55 70 */
tree.insert(50);
tree.insert(40);
tree.insert(35);
tree.insert(45);
tree.insert(60);
tree.insert(55);
tree.insert(70);
tree.secondLargest(tree.root);
}
}
Output:
The second largest element is 60
Frequently Asked Questions
What is a Binary search tree?
A Binary Search Tree (BST) is a node-based tree data structure. In BST, the left and right subtree will also be a binary search tree. The right subtree of a node will contain nodes with values greater than the node's value, and the left subtree will have nodes with values lesser than the node's value.
What are the traversal techniques in BST?
There are three traversal techniques: Inorder traversal, Preorder traversal, and Postorder traversal.
What are the primary operations in a binary tree?
The main operations in binary tree are insert, search and delete.
What is the parent and child node in BST?
The predecessor of any node is called the parent node. The node that is the immediate successor of a node is called the child node. Nodes with no children are called leaves or external nodes.
What's the difference between a Binary tree and a Binary search tree?
In BST, the values of the left subtree of a node should be lesser than the parent node, and the right subtree values should be greater. But when it comes to a binary tree, there is no such requirement.
Conclusion
We have learned how to find the second largest element in BST using reverse in-order traversal. To get a better understanding, look into How to get better at DSA for Beginners
Check out this problem - Reverse Nodes In K Group
Refer to our Test Series, problems lists, problems, participate in contests, and take a look at our courses that will help you become proficient in DSA in Python, C++, Java, and Competitive programming. These Interview experiences will give you a heads-up on what you must prepare for!
Look into our Library to explore more courses!
Thank you!