Introduction
This blog will discuss a Binary Tree problem. We are provided with a binary tree and the task is to find the sum of all right leaves in a given binary tree. The term "right leaf node" refers to a leaf node that is the right child of a parent. We must constantly check to see if the current node has any right children that are also leaf nodes while traversing. If the node has, we combine the cumulative sum with the appropriate child node value.
Problem Statement
Ninja has a binary tree. The total nodes in the tree are n. He gave the tree to you. He said he wanted to check the sum of all right leaf nodes of the respective binary tree. But, the problem is that he cannot check it alone as he is busy with other work. Can you help him with the situation and Calculate the sum of all right leaves nodes in the given binary tree.
Before deep-diving into the solution to this problem, we should look at some examples to help us understand the situation better.
Sample Examples
Example 1:
Here, as shown in the diagram we have two right leaf nodes i.e. 3 and 6
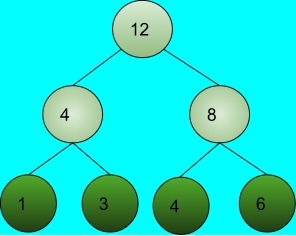
Output:
9
Explanation:
The Right leaf nodes of the tree are: 3, 6
Therefore, Sum = 3 + 6 = 9
Example 2:
Here, as shown in the diagram we have only one right leaf node i.e. 6
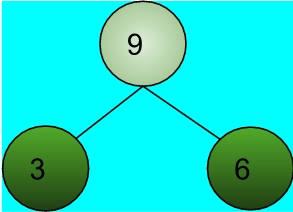
Output:
6
Explanation:
The right leaf node of the tree is: 6
Therefore, Sum = 6Approach 1: Using recursion
The goal is to move up the tree starting at the root and determine whether or not each node is a leaf node. Add the right leaf's data to the sum variable if the node is the right leaf.
Algorithm
- From root to leaf, we will traverse the tree.
- Verify whether or not the node is a leaf node.
- Add a node to the sum if it is a left leaf node.
- After traversing the entire tree. Print Sum.
Implementation
#include <iostream>
using namespace std;
//Using recursion to find the sum of all right nodes of the binary tree
struct Node{
int key;
struct Node* left, *right;
};
Node *newNodeofBT(char k){
Node *node = new Node;
node->key = k;
node->right = node->left = NULL;
return node;
}
bool isLeafNodeofBT(Node *node){
if (node == NULL)
return false;
if (node->left == NULL && node->right == NULL)
return true;
return false;
}
int findRGTLeavesSum(Node *root){
int sum = 0;
if (root != NULL){
if (isLeafNodeofBT(root->right))
sum += root->right->key;
else
sum += findRGTLeavesSum(root->right);
sum += findRGTLeavesSum(root->left);
}
return sum;
}
//Main Function of the Program
int main(){
struct Node *root = newNodeofBT(5);
root->left = newNodeofBT(4);
root->right = newNodeofBT(6);
root->left->left = newNodeofBT(2);
root->left->right = newNodeofBT(1);
root->right->left = newNodeofBT(9);
root->right->right = newNodeofBT(7);
cout<<" Sum of all right leaves of the Binary tree is "<<findRGTLeavesSum(root);
return 0;
}
Output
Sum of all right leaves of the Binary tree is 8
Complexity Analysis
Time Complexities: O(n), The recursive function takes O(n) time to traverse the whole binary tree. Here n is the number of nodes in the binary tree.
Space Complexities: O(n), The stack used in this recursive function takes O(n) extra space. So the space complexity is O(n).





